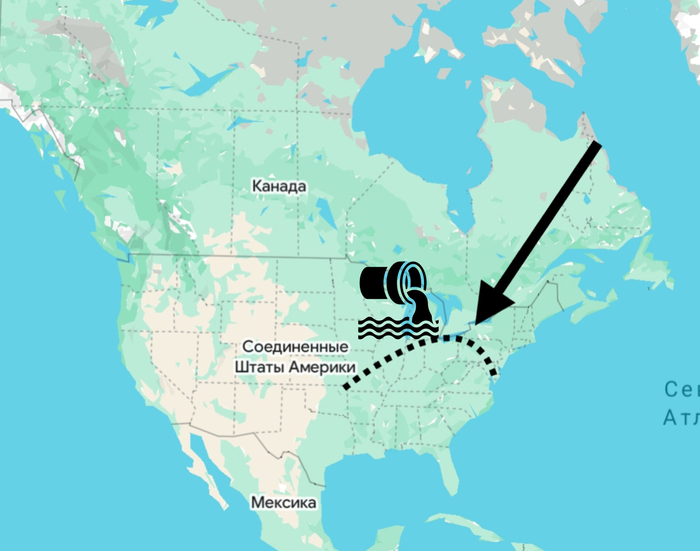
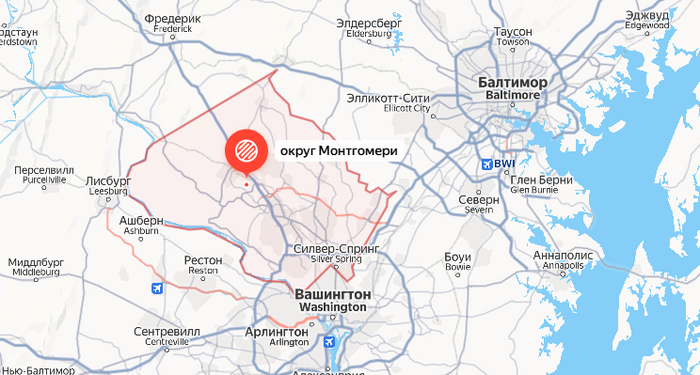
В США случился масштабный прорыв канализации на 240 миллионов галлонов. Это произошло всего в 8 км вверх по течению от столицы - Вашингтона (в округе Монтгомери). Вот здесь.
Чтобы понять, насколько 240 миллионов галлонов это много, для начала нужно перевести галлоны в литры. И здесь буквально несколько слов о галлонах. Эту меру объёма многие слышали из сообщений например о стоимости бензина в США.
Но в разных странах галлоны имеют разные значения. Например существует британский галлон и американский галлон. Это разные галлоны. Вообще его придумали триста лет назад и изначально измеряли им объём бочек с пивом и вином.
Англичане долго совершенствовали эту систему и придумали так:
кукурузный галлон - 4,4 литра
винный галлон - 3,7 литра
специальный галлон для эля - 4,6 литра
Ну и во всех своих колониях ввели подобную систему. Однако чтобы не путаться, они остановились на цифре в 4,5 литра за галлон.
Так вот когда США стали самостоятельными, они систему галлонов оставили, но ввели своё значение - 3,7 литра. То есть взяли за основу значение винного британского галлона.
Таким образом, сегодня есть так называемый британский галлон (4,5 литра) и его используют (или до недавних пор использовали) в Канаде, Ирландии, Новой Зеландии, Австралии и некоторых странах, где британский монарх до сих пор формально числится правителем.
А вот американский галлон в 3,7 литра популярен в странах Латинской Америки и в самих США.
Однако вернёмся к новости о том, что в Потомак вылилось 240 миллионов галлонов нечистот. Этот объём нужно считать именно в американской системе. Но как понять, насколько это вообще много или мало?
Давайте для простоты переведём галлоны в привычные нам литры.
240 000 000 галлонов×3,785=𝟗𝟎𝟖 𝟒𝟎𝟎 𝟎𝟎𝟎 литров. Почти миллиард литров.
Чтобы лучше представить себе такой объем, давайте приведем пример.
Все видели стандартный олимпийский бассейн.
Длина - 50 метров
Ширина - 25 метров
Глубина - 2 метра
Бывают и больше, но оттолкнёмся от него.
Объем воды в таком бассейне хорошо известен. В сети уже много раз приводили цифры.
Как мы знаем, в одном кубометре 1000 литров. Соответственно 1000*2500 и получаем 2,5 миллиона литров воды в одном олимпийском бассейне.
Теперь берём всё вылитое из канализации в Потомак, 𝟗𝟎𝟖 𝟒𝟎𝟎 𝟎𝟎𝟎 литров, и делим на 2,5 миллиона литров. Выходит, что в реку утекло содержимое объёмом в 363 олимпийских бассейна.
Представьте себе большой современный жилой комплекс где-нибудь в Москве с десятком многоэтажных домов, парком и инфраструктурой.
Допустим каждая квартира ежедневно потребляет примерно 200 литров воды. Люди умываются, принимают душ, моют посуду, стирают одежду... Так вот чтобы все эти десять домов израсходовали весь объём воды слитый в Потомак, им понадобилось бы 3,5 года.
То есть миллиард литров - это реально ощутимо. Вот ещё несколько примеров:
- Один крупный металлургический комбинат тратит около 10 миллионов литров воды в сутки. Следовательно, миллиард литров обеспечит потребности комбината примерно на сто дней непрерывной работы.
- Или возьмём средний объем обычного озера (например, небольшого лесного водоема) - около 100 миллиона литров. Значит, миллиард литров составит целое искусственное озеро, равное десяти таким озерам.
- Можно посчитать и так. Среднее потребление воды марафонцем составляет около 1 л воды в час.
Хотя здесь всё очень индивидуально, но всё же. Таким образом, миллиард литров хватит для снабжения водой участника марафона на протяжении двух человеческих жизней, если бежать, плыть и ехать не велосипеде без остановки на сон, обед и работу.
-Ну и последний пример. Ежедневный водозабор крупной европейской столицы, например Москвы, составляет около 3 миллионов кубометров воды в сутки (3 миллиарда литров). Один миллиард литров покрывает потребности такого мегаполиса примерно на 8 часов. Не мало. Цифры кажутся гигантскими, особенно в сравнении со столицами.
Так вот представьте, что в реку одномоментно вылили содержимое такого огромного мегаполиса. Несомненно определённый ущерб имеется, но он вряд ли будет непоправимым. Дело в том, что река Потомак за всю свою историю заработала репутацию очень грязной реки. Всё дело в том, что на ней построили несколько крупных городов - Вашингтон, Александрия, Фредерик и тд. И она очень быстро начала загрязняться. Особенно в 20 веке. В какой-то момент значительную часть просто затянуло зеленью. А учитывая то, что часть Вашингтона и сопредельного Штата, в качестве основного источника воды использовали Потомак, это доставляло грандиозные проблемы. Поэтому начали строить очистные, отводы, систему канализации и так далее, после чего река пришла в норму. Однако инженерные системы долгое время не ремонтировались и как следствие, произошёл прорыв канализации прямо в реку, со всеми, в прямом смысле, вытекающими последствиями.
Если вам понравилась статья и вы хотите видеть в ленте больше таких материалов, просьба поставить палец вверх и подписаться.
Дорогие друзья, также приглашаем вас заглянуть в наш телеграм, VK, MAX и Sponsr.ru.
А если хотите поощрить, то легко это можете сделать здесь.