В предыдущей публикации я предложил модель конечного автомата на кольце Z_7, которая неожиданно выдала число 108. Скептики в комментариях закономерно посчитали это подгонкой под ответ.
Принимаю вызов. Сегодня мы уберем мистику и применим единый алгоритм ко всем системам от L2 до L7. Мы увидим, как потеря хиральности в L4 ломает емкость, почему L5 — это монолит, и почему 108 — это не случайность, а точка сходимости Процесса и Структуры.
1. Аксиоматика (Rules of Engagement)
Мы используем класс систем Depth-2 Finite Automata. Чтобы разговор был предметным, зафиксируем три правила, которые определяют «физику» нашей модели:
[A1] Аксиома Глубины (Depth-2)
Состояние системы — это не скаляр (точка), а вектор. Как в физике волн (амплитуда + фаза), минимальный квант информации двумерен. Внутренняя память ячейки — это торсор над Z_r x Z_r.
[A2] Аксиома Монолитности (Prime Rhythm)
Рабочий ритм (r) — это максимальное простое число (p), делящее порядок группы. Это исключает «дребезг» и распад системы на подкомпоненты.
[A3] Аксиома Хиральности (Chirality)
Направление времени различимо только при r >= 3.
Total = Base * Fiber Total = (s * r * o) * (r^2) Где: s - количество струн (независимых орбит) r - атомарный ритм (простое число) o - ориентация (1 или 2) r^2 - внутренняя память (фибра)
2. Лабораторная работа: Прогон по спектру
Применим формулу к разным кольцам (локам). Посмотрим, совпадет ли математика с реальностью.
Ядро R = 2. Ритм r = 2.
Струны: Одна (0 -> 1). s = 1.
Ориентация: o = 1 (ритм 2).
Расчет: (1 * 2 * 1) * 2^2 = 2 * 4 = 8.
Это классический байт (2 состояния бита на 4 состояния контекста).
L4: Аномалия Маятника (Z_4)
Ядро R = 4. Ритм r = 2 (макс. простое в четверке).
Мотор (+2) разбивает ядро на 2 струны: {0,2} и {1,3}. s = 2.
Ориентация: o = 1 (ритм 2).
Расчет: (2 * 2 * 1) * 2^2 = 4 * 4 = 16.
Алгебра неумолима: в режиме маятника (туда-сюда) хиральность исчезает, и емкость «схлопывается».
Ядро R = 5. Ритм r = 5. s = 1. o = 2.
Расчет: (1 * 5 * 2) * 5^2 = 10 * 25 = 250.
Мощная система, но из-за одной струны (s=1) ей не хватает гибкости для параллельных процессов.
3. Точка сходимости: Загадка L6 и L7
Почему именно 108? Посмотрим на подписи двух систем:
L6 (Процесс / Время): Кольцо (Z_6, +).
L7 (Структура / Смысл): Группа (Z_7*, *).
R = 6 (числа 1..6). Ритм r = 3.
Мотор (*2) дает 2 струны: {1,2,4} и {3,6,5}. s = 2. o = 2.
Расчет: (2 * 3 * 2) * 3^2 = 12 * 9 = 108.
Вывод: Системы L6 и L7 — это кинематические близнецы. Число 108 — это не магия, а емкость конфигурации «2 струны по 3 такта» в классе Depth-2.
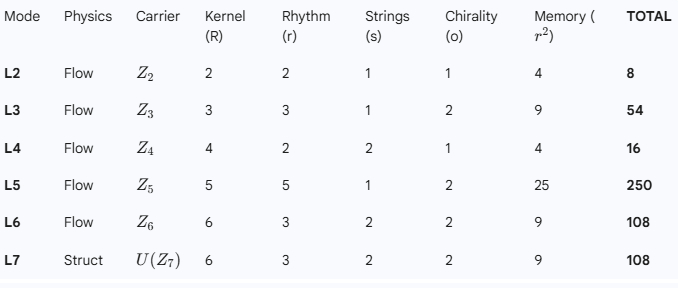
4. Сводная таблица (The Diamond Table)
+------+--------+---------+---+-------+---+---+---+------+-------+-------+
| MODE | Physics| Carrier | R | Motor | r | s | o | Base | Fiber | TOTAL |
+------+--------+---------+---+-------+---+---+---+------+-------+-------+
| L2 | Flow | Z_2 | 2 | +1 | 2 | 1 | 1 | 2 | 4 | 8 |
| L3 | Flow | Z_3 | 3 | +1 | 3 | 1 | 2 | 6 | 9 | 54 |
| L4 | Flow | Z_4 | 4 | +2 | 2 | 2 | 1 | 4 | 4 | 16 |
| L5 | Flow | Z_5 | 5 | +1 | 5 | 1 | 2 | 10 | 25 | 250 |
| L6 | Flow | Z_6 | 6 | +2 | 3 | 2 | 2 | 12 | 9 | 108 |
| L7 | Struct | U(Z_7) | 6 | *2 | 3 | 2 | 2 | 12 | 9 | 108 |
+------+--------+---------+---+-------+---+---+---+------+-------+-------+
5. Что это дает инженеру?
Архитектура Шардинга: Модели L4, L6 и L7 показывают, как математически строго разделить поток данных на независимые шарды (струны s=2), гарантируя отсутствие «гонок» (race conditions).
Несжимаемость (Irreducible Complexity): Систему на 108 состояний нельзя «оптимизировать» до 18, выкинув индекс струны. Без него автомат перестает быть детерминированным.
Закон Квадрата: Сложность внутреннего состояния (кэша/памяти) растет как квадрат ритма (r^2). Это базовая эвристика при проектировании State Machines.
Заключение
Мы начали с подозрения в нумерологии, а закончили строгой таблицей классов конечных автоматов. Число 108 оказалось не «космической вибрацией», а надежным инженерным пределом для систем с двумя потоками и тройным ритмом.
Ирония в том, что древние, используя число 108, интуитивно работали с идеальной математической моделью, которую мы только что описали на языке теории групп.
Приложение: Формальное обоснование (ASCII)
(Для тех, кто готов спорить с аксиомами)
[A6] Macro-Invariant Axiom: Пусть T - шаг автомата на полном слое Q_full. pi_base( T^(r^2)(q) ) = NEXT( pi_base(q) ) Это значит, что внутренний механизм обязан провернуться r*r раз, прежде чем внешняя фаза (Base) сдвинется на один шаг. Это жестко фиксирует размер фибры как r^2.
Хотите проверить это на своих данных? Я подготовил MP_YANTRA_CORE_iter220.zip. Загрузите его в GPT и выполните команду: Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md.
Автор статьи — Руслан Абдуллин. Вступайте в мой тг-канал ⚛️
Для ЛЛ
Уровень 1: Инженерный минимум
Число 108 — это не магия, а технический стандарт. Автор доказал, что любая система (хоть биты в памяти, хоть логика смыслов), построенная на «тройном ритме» и «двух потоках», обязана иметь емкость 108.
Это как формат листа А4: он такой не из-за мистики, а потому что так удобнее и математически экономнее. 108 — это «точка сборки» между линейным временем и циклической структурой.
Уровень 2: Суть метода (Для тех, кто прочитал статью)
Проблема: Почему 108 возникает и в L6 (время), и в L7 (смыслы)? Решение: Сравнение «кинематических подписей» всех систем от L2 до L7.
L2 (8 состояний): Фундамент. 1 струна, ритм 2. Это наш привычный байт.
L4 (16 состояний): Баг маятника. Здесь система «тупеет», потому что при ритме 2 нельзя отличить «вперед» от «назад». Ориентация схлопывается в единицу.
L6 и L7 (108 состояний): Идеальный баланс. Здесь впервые встречаются 2 независимых потока (шарда) и тройной ритм.
Формула: Total = (Струны * Ритм * Ориентация) * Ритм^2.
Для L6 и L7 расчет идентичен: (2 * 3 * 2) * 3^2 = 12 * 9 = 108. Это инвариант.
Уровень 3: Для богов алгебры (Formal Proof)
Тезис: Существует естественный изоморфизм между конфигурационными пространствами систем типа (s,r,o,d) при d=2.
Доказательство (ASCII): Пусть динамика системы задана действием циклической группы H порядка r на ядре R. По теореме Лагранжа ядро распадается на s = |R|/|H| орбит. Фазовое пространство (Base) определяется как расширение X / H группой автоморфизмов ориентации Aut(H). При r=2 расширение тривиально (o=1), при r>=3 — нетривиально (o=2).
Внутренняя емкость (Fiber) фиксируется аксиомой Depth-2 как торсор над H x H. Следовательно, полная мощность системы |Q| является функцией только от инвариантов подгруппы: |Q| = o * [R:H] * |H| * |H|^2 = o * |R| * |H|^2
Для L6 (Z_6, +) и L7 (Z_7*, *) имеем: |R|=6, |H|=3, o=2. |Q| = 2 * 6 * 3^2 = 108.
Q.E.D. Число 108 — это просто порядок стабилизатора для систем класса (2,3,2,2).
Хотите проверить теорию на своих структурах данных? Я подготовил MP_YANTRA_CORE_iter220.zip. Загрузите его в чат и напишите: Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md.