Наука | Научпоп

Автор: Денис Аветисян

Исследование демонстрирует инновационный метод селективной генерации и контроля хиральности межслойных экзитонов, заключенных в моаровых структурах, с использованием хиральных фононов.

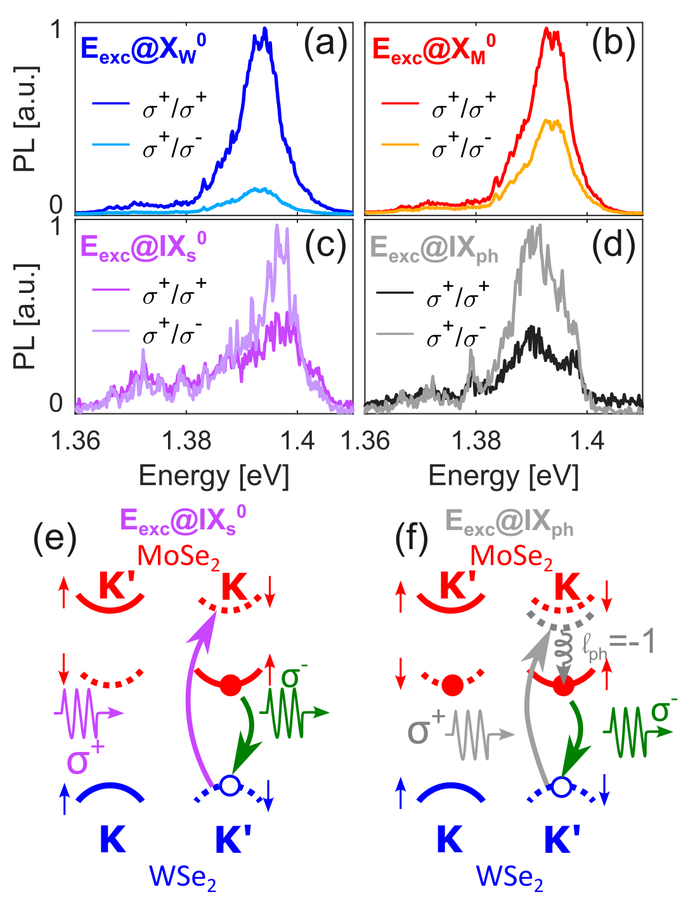
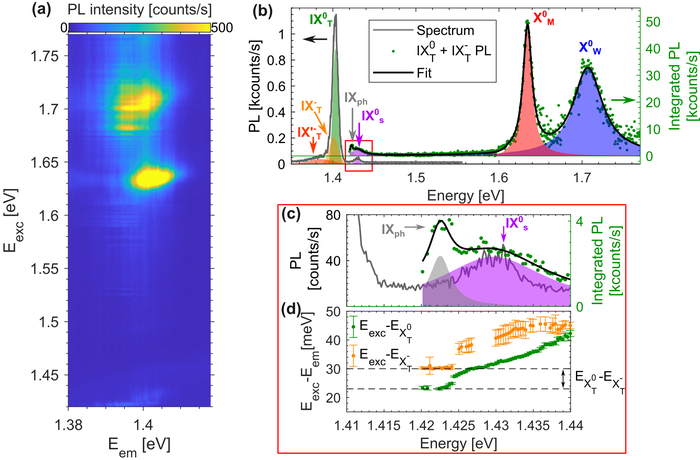
Исследование спектров фотолюминесценции межслойных экситонов выявило, что резонансное возбуждение, настроенное на внутрислойные экситоны WSe₂ и MoSe₂ или на сингулетные межслойные экситоны, приводит к эмиссии, подчиняющейся правилам оптического отбора для прямых электронных переходов, в то время как возбуждение, опосредованное хиральными фононами, вызывает циркулярно-поляризованную эмиссию, отражающую перенос псевдо-углового момента от фононов к экситонной системе.

Фотовозбуждение захваченных межслойных экзитонов посредством хиральных ин-планных оптических фононов открывает возможности для управления их поляризацией и характеристиками излучения.

Несмотря на значительный прогресс в управлении квантовыми свойствами полупроводниковых гетероструктур, селективная генерация отдельных экситонов остается сложной задачей. В работе, посвященной 'Photoexcitation of moiré-trapped interlayer excitons via chiral phonons', продемонстрирован новый механизм фотовозбуждения межслойных экситонов, локализованных в сверхрешетках моаре, посредством хиральных оптических фононов. Установлено, что данный процесс обеспечивает контролируемое возбуждение экситонов с определенной хиральностью и узкой спектральной шириной излучения. Открывает ли это путь к созданию новых устройств для спинтроники и квантовой фотоники на основе TMD моаре-систем?

Как создать свет из ничего: Новые горизонты взаимодействия света и материи

Традиционные двумерные материалы, несмотря на свои уникальные свойства, предлагают ограниченные возможности для управления характеристиками возбужденных состояний, известных как экситоны, что препятствует развитию передовых оптоэлектронных устройств. Однако, создание ван-дер-ваальсовских гетероструктур и, в особенности, моаровых суперрешеток, открывает принципиально новые пути для целенаправленной инженерии взаимодействия света и материи. Эти структуры позволяют тонко настраивать энергетические уровни материалов, выстраивая их так, чтобы свет эффективно взаимодействовал с электронными состояниями. Суть заключается в создании периодических структур, где два материала, слегка сдвинутые относительно друг друга, образуют узор, подобный моаровому эффекту, который можно увидеть, когда два экрана накладываются друг на друга. Этот эффект создает области с измененными электронными свойствами, усиливая или ослабляя взаимодействие света с материалом, и позволяя создавать материалы с заранее заданными оптическими характеристиками. Таким образом, моаровые суперрешетки представляют собой перспективную платформу для разработки новых поколений оптоэлектронных устройств с улучшенными характеристиками и функциональностью.

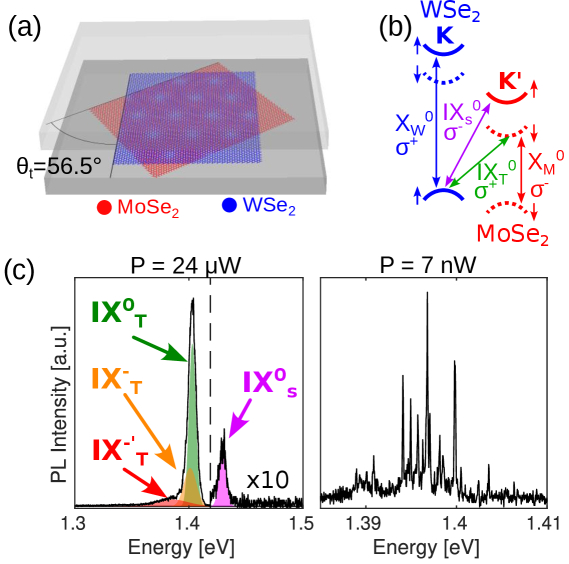
В гетероструктуре из 2H-MoSe2/WSe2, заключенной в hBN, наблюдается выравнивание электронных зон типа II и спин-долинная конфигурация, приводящая к появлению ярких экситонных состояний внутри слоев WSe2 и MoSe2, а также спин-синглетных и спин-триплетных межслойных экситонов, зарегистрированных в спектрах фотолюминесценции при различных мощностях возбуждения P=24mu W и P=7nW.

Межслоевые Экситоны: Квантовые Ловушки для Света

В гетероструктурах, состоящих из слоев различных материалов, формируются межслоевые экситоны - пары электрон-дырка, связанные между собой, но находящиеся в соседних слоях. Особая структура этих материалов создает так называемый «потенциал моаре», который действует как крошечная ловушка для экситонов, заставляя их энергию принимать лишь определенные, дискретные значения. Это приводит к усилению оптических свойств материала, делая его более эффективным в работе со светом. Важную роль в поведении этих экситонов играет величина, известная как фактор Ланде, и явление поляризации долин, определяющие спиновое и долинное состояние экситонов. Эти характеристики открывают захватывающие возможности для создания новых устройств в областях спинтроники и долинной электроники, где информация кодируется не только зарядом, но и спином и долиной электронов.

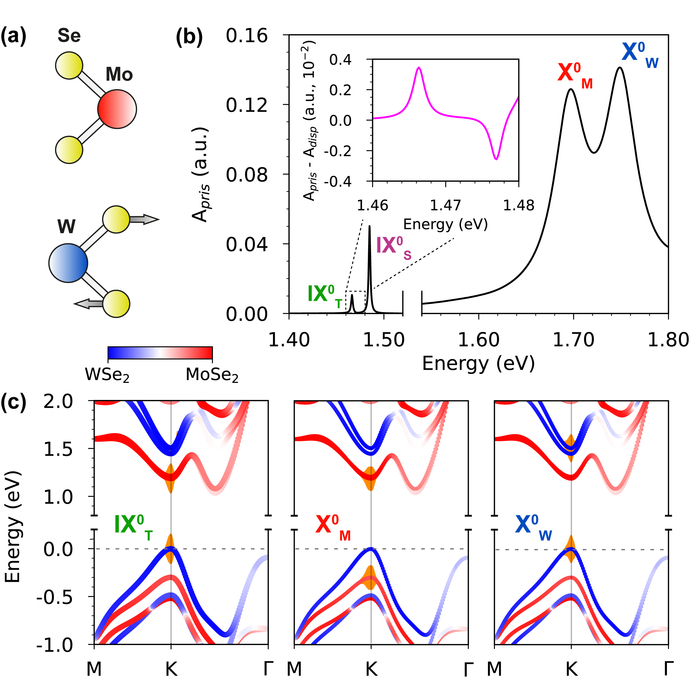
Анализ спектра поглощения гетероструктуры MoSe2/WSe2 показал сильное взаимодействие между межслойными экситонами и колебаниями E′ᵖʳⁱᵐᵉ моды, что подтверждается изменением интенсивности пика IXT0⁰T и картированием экситонных состояний на зонную структуру слоев.

Фононно-селективное возбуждение: ключ к управлению светом в материалах

Традиционные методы возбуждения света в материалах, основанные на прямом поглощении фотонов, зачастую лишены избирательности. Однако существует альтернативный путь - возбуждение с помощью фононов, квантов колебаний кристаллической решетки. Взаимодействие между возбужденными состояниями - экситонами - и фононами позволяет избирательно возбуждать определенные состояния материала. Особую роль в этом процессе играет оптический фонон E'', обладающий уникальным “псевдо-угловым моментом”, который влияет на импульс и поляризацию экситона. Эффективность и избирательность такого фононно-опосредованного возбуждения напрямую зависят от силы связи между экситонами и фононами; в частности, для оптимального результата используется энергия фонона в 23 мегаэлектронвольта. Это позволяет более точно контролировать световые процессы внутри материала и открывает новые возможности для создания оптических устройств.

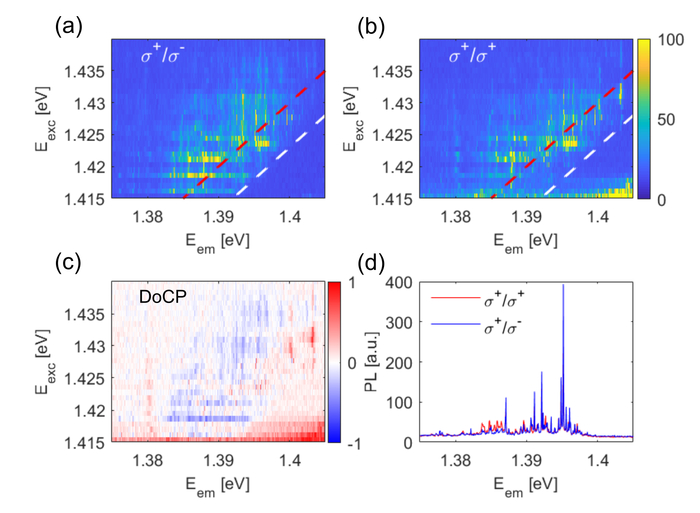
Анализ поляризованной фотолюминесценции, возбужденной циркулярно поляризованным светом σ⁺, показывает, что энергия одиночных излучателей лучше соответствует более низкому уровню энергии Eₑₓc - 30 мэВ, что указывает на формирование трионов, а зависимость доличной поляризации от энергии возбуждения демонстрирует ее зависимость от энергетического положения трионных состояний, подтвержденную примером спектра одиночного излучателя при Eₑₓc=1.4226 эВ.

Управление свойствами экситонов: угол скручивания и поляризация

Исследования показывают, что угол между слоями материала оказывает существенное влияние на поведение экситонов - особых квазичастиц, определяющих оптические свойства. Изменение этого угла приводит к формированию уникального рельефа потенциальной энергии, который, подобно ландшафту, влияет на движение и энергию экситонов. Для точного определения угла скручивания используется метод поляризационно-зависимого генерации второй гармоники, позволяющий получить важную информацию о структуре материала. Неоднородность угла скручивания может приводить к образованию областей с различными свойствами экситонов. В проведенных экспериментах удалось достичь угла скручивания в 56.5 ± 0.8 градусов, что минимизирует образование таких неоднородных областей. Более того, управляя углом скручивания, можно контролировать спиральную поляризацию испускаемых фотонов, что позволяет получить представление об атомной структуре материала и расположении атомов в слоях.

Анализ спектров фотолюминесценции возбужденного лазером образца показал зависимость интенсивности пиков IXT0⁰T и IXT⁻T от энергии возбуждения, которая была успешно аппроксимирована четырьмя лоренциальными пиками, что позволило определить энергии возбуждения для каждого пика.

За гранью основ: к созданию передовых оптоэлектронных устройств

Исследование характеристик особых квазичастиц - экситонов, захваченных в моаровых структурах, стало возможным благодаря использованию конфокальной фотолюминесценции. Наблюдение так называемого антибунчинга фотонов, явления, подтверждающего квантовую природу этих экситонов, открывает перспективы для создания источников одиночных фотонов - ключевого элемента квантовых технологий. Эксперименты также показали, что управление свойствами экситонов возможно через создание устройств с управляемой концентрацией заряженных экситонов, известных как трионы. В ходе исследований была определена энергия связи триона - всего 7 мегаэлектронвольт, что указывает на потенциал для тонкой настройки их свойств. Взаимодействие между материаловедением, контролем над экситонами и технологией изготовления устройств знаменует наступление новой эры в создании передовых оптоэлектронных приборов.

Исследование взаимодействия экситонов и хиральных фононов демонстрирует изящную сложность, скрытую в, казалось бы, простых гетероструктурах. Стремление к управлению спином и оптическими свойствами экситонов через фононное возбуждение - это не просто научный поиск, но и стремление к минимализму в управлении материей. Как заметил Луи де Бройль: «Каждый физик знает, что свет ведет себя то как волна, то как поток частиц». Эта двойственность отражает саму суть изучаемых явлений - волновые свойства фононов, взаимодействующие с корпускулярной природой экситонов, создавая новые возможности для контроля над состоянием вещества. Ясность - это минимальная форма любви, и в данном исследовании она проявляется в стремлении к точному пониманию фундаментальных взаимодействий.

Куда Ведет Дорога?

Представленная работа, несомненно, открывает путь к управлению хиральностью межслойных экситонов в гетероструктурах. Однако, стоит признать, что избирательное возбуждение посредством хиральных фононов - это лишь первый шаг. Более глубокое понимание механизмов релаксации, особенно влияния дефектов и примесей на когерентность экситонов, остается критически важной задачей. Стремление к совершенству в этой области заключается не в увеличении числа параметров, а в их радикальном сокращении - в выявлении истинных степеней свободы, определяющих поведение системы.

Очевидным направлением для дальнейших исследований является поиск новых материалов, в которых хиральные фононы проявляют более сильное взаимодействие с межслойными экситонами. Важно также рассмотреть возможность использования этого механизма для создания спиновых токов и других когерентных эффектов. Попытки усложнить схему, добавив дополнительные слои или управляющие поля, неизбежно приведут к увеличению шума и снижению точности. Истинный прогресс заключается в простоте и элегантности.

В конечном итоге, задача состоит не в создании искусственных структур, имитирующих природные явления, а в понимании фундаментальных принципов, управляющих поведением материи. Каждый комментарий к коду - это признание его несовершенства; каждая добавленная функция - потенциальный источник ошибок. Совершенство - это исчезновение автора, растворение в объекте исследования.

Полный обзор с формулами: lospopadosos.com/upravlyaya-svetom-i-spinom-novye-vozmozhnosti-dlya-mezhslojnyh-eksitonov

Оригинал статьи: https://arxiv.org/pdf/2512.21125.pdf

Связаться с автором: linkedin.com/in/avetisyan

Автор: Денис Аветисян

Исследователи представили новую модель, способную выполнять квантовый поиск, используя возможности больших языковых моделей.

Исследование демонстрирует возможности модели GroverGPT в моделировании квантового поиска, оценивая её эффективность, обобщающую способность для систем с различным числом кубитов, сравнивая результаты с классическими подходами и выявляя роль разработки запросов, что позволяет рассматривать GroverGPT как перспективный инструмент для преодоления разрыва между квантовыми и классическими вычислениями.

Представлена GroverGPT - языковая модель с 8 миллиардами параметров, демонстрирующая перспективные результаты в симуляции алгоритма Гровера и превосходящая классические модели в задачах обучения квантовым алгоритмам.

Несмотря на потенциал квантовых вычислений, классическое моделирование квантовых алгоритмов остается сложной задачей. В работе «GroverGPT: A Large Language Model with 8 Billion Parameters for Quantum Searching» представлена новая модель, использующая большие языковые модели для симуляции алгоритма поиска Гровера. Разработанная модель GroverGPT, основанная на архитектуре LLaMA с 8 миллиардами параметров, демонстрирует высокую точность и обобщающую способность в задачах квантового поиска, превосходя универсальные модели, такие как GPT-4o. Может ли такой подход открыть новые пути для изучения границ классической симуляции квантовых вычислений и ускорить разработку квантовых алгоритмов?

Квантовый поиск: преодолевая экспоненциальную сложность

Эффективный поиск в несортированных базах данных является фундаментальной задачей информатики, значимость которой неуклонно возрастает в эпоху больших данных. Классические алгоритмы сталкиваются с экспоненциальной сложностью данной задачи, требующей квадратичного времени выполнения - O(n²). Алгоритм Гровера предлагает квадратичное ускорение, снижая сложность до O(√n), однако его практическая реализация на современных и ближайших квантовых аппаратных платформах представляет собой существенную проблему, ограничивающую потенциал данной технологии в решении задач поиска.

ГроверGPT: Языковая Модель для Квантового Моделирования

Разработана модель ГроверGPT, языковая модель с 8 миллиардами параметров, предназначенная для симуляции алгоритма Гровера и объединяющая теоретические концепции с практическими реализациями. В основе архитектуры лежит LLaMA, а ключевым элементом является применение методов обработки естественного языка для трансляции квантовых операций в формат, понятный классическим вычислительным системам. Для определения квантовых схем ГроверGPT использует язык QASM в качестве стандартизированного входного формата, что обеспечивает гибкость и доступность процесса моделирования. Это позволяет исследователям и разработчикам эффективно изучать и оптимизировать квантовые алгоритмы, используя возможности классических вычислений для симуляции сложных квантовых систем и проведения предварительных тестов перед переходом к реальным квантовым устройствам.

Модель GroverGPT предварительно обучается путем комбинирования данных, сгенерированных алгоритмом Гровера на симулированном квантовом компьютере, вероятностных распределений результатов измерений и соответствующего QASM-кода, что позволяет ей использовать архитектуру Llama-3.1-8B и эффективно решать задачи квантовых вычислений.

Оценка точности и достоверности моделирования

Эффективность модели GroverGPT оценивается с помощью метрик, таких как точность, определяющая корректность результатов поиска. Для детального анализа расхождений между предсказанными и фактическими квантовыми состояниями используются показатели неточности и значительной неточности. Исследование демонстрирует, что GroverGPT способен достигать почти 100%-ной точности в симуляциях поиска Гровера для систем в 6 и 10 кубитов, при обучении на данных, включающих 4 и более кубитов. Более того, модель поддерживает точность выше 95% для систем, насчитывающих более 20 кубитов, при обучении на данных из 3-6 кубитов, что свидетельствует о ее сильных обобщающих способностях. Для сравнения, OpenAI GPT-4o демонстрирует лишь 45%-ную точность при решении тех же задач, что подчеркивает превосходство GroverGPT в данной области.

Эксперименты с GroverGPT демонстрируют высокую точность и обобщающую способность на квантовых задачах поиска, подтвержденную сходимостью обучения, сравнительным анализом с другими моделями (включая GPT-4o) и стабильной производительностью при различных гиперпараметрах и масштабировании до 20 кубитов.

Преодолевая границы классического моделирования: потенциал GroverGPT

Традиционные методы моделирования квантовых схем, такие как прямое моделирование с использованием векторного состояния, сталкиваются с экспоненциальным ростом вычислительных затрат, что делает их непрактичными для работы со сложными квантовыми вычислениями. Альтернативные подходы, например, тензорные сети, предлагают компромисс между объемом используемой памяти и точностью, однако и они испытывают трудности при моделировании действительно сложных систем. В этой связи, GroverGPT представляет собой перспективную альтернативу, предлагая потенциально масштабируемый и эффективный способ моделирования и анализа алгоритма Гровера. Эффективное моделирование квантовых алгоритмов на классическом оборудовании посредством GroverGPT способно значительно ускорить разработку и валидацию новых квантовых алгоритмов, открывая новые возможности для исследований в области квантовых вычислений и позволяя более глубоко понять их потенциал.

В представленной работе демонстрируется способность больших языковых моделей к освоению и симуляции квантовых алгоритмов, в частности, алгоритма Гровера. Это подчеркивает, что версионирование, как форма памяти, позволяет модели не просто запоминать последовательности, но и экстраполировать знания на новые задачи. Как однажды заметил Ричард Фейнман: «Если вы не можете объяснить что-то простыми словами, значит, вы сами этого не понимаете». В данном контексте, GroverGPT демонстрирует понимание принципов квантового поиска, превосходя классические модели в специфических задачах, что подтверждает потенциал LLM как среды для изучения и симуляции сложных систем. Стрела времени в данном случае указывает на необходимость постоянного рефакторинга и улучшения алгоритмов симуляции.

Что впереди?

Представленная работа демонстрирует любопытную тенденцию: большие языковые модели, подобные GroverGPT, способны осваивать и воспроизводить логику квантовых алгоритмов, превосходя в этой задаче универсальные вычислительные модели. Однако, эта способность, словно отблеск света в конце туннеля, лишь подчеркивает глубину нерешенных вопросов. Логирование процесса обучения модели - это, по сути, хроника её жизни, но что скрывается за этой хроникой? Какова истинная природа "понимания" квантовых принципов языковой моделью?

Развертывание модели - это лишь мгновение на оси времени, а проверка её обобщающей способности - попытка предсказать её поведение в неизведанном будущем. Очевидно, что вопрос классической симулируемости квантовых вычислений остаётся открытым, и GroverGPT лишь добавляет новую главу в эту дискуссию. Следующим шагом видится не просто увеличение количества параметров модели, а углубленное исследование её внутренней структуры, выявление механизмов, лежащих в основе её способности к квантовому моделированию.

В конечном итоге, все системы стареют - вопрос лишь в том, делают ли они это достойно. Истинный прорыв, вероятно, лежит не в создании всемогущего квантового компьютера, а в создании интеллектуальной системы, способной эффективно использовать ограниченные ресурсы, будь то классические или квантовые. И в этом контексте, GroverGPT - лишь первый, хотя и многообещающий, шаг на долгом пути.

Полный обзор с формулами: denisavetisyan.com

Оригинал статьи: https://arxiv.org/pdf/2501.00135.pdf

Связаться с автором: linkedin.com/in/avetisyan

Вселенная расширяется - это мы знаем со времён Эдвина Хаббла, который в 1929 году показал, что галактики удаляются друг от друга, словно точки на надувающемся шаре. Но в конце XX века астрономы столкнулись с шокирующим открытием: расширение не замедляется под действием гравитации, как ожидалось, а ускоряется. Эта загадочная сила, толкающая космос в стороны с всё большей скоростью, получила название тёмной энергии. Она составляет около 68% всей массы-энергии Вселенной, но остаётся одной из величайших тайн современной физики. Почему Вселенная ускоряется? Что скрывается за этой невидимой силой? И что её существование говорит о судьбе космоса и природе реальности?

Открытие ускорения

История тёмной энергии началась в 1998 году, когда две независимые команды астрономов - одна под руководством Сола Перлмуттера, другая - под руководством Адама Рисса и Брайана Шмидта - изучали сверхновые типа Ia - "стандартные свечи" космоса, чья яркость позволяет измерять расстояния до далёких галактик. Далёкие сверхновые казались тусклее, чем предсказывали модели, что означало, что расширение Вселенной не замедляется, как ожидалось, а ускоряется.

Это открытие перевернуло космологию. За него в 2011 году была вручена Нобелевская премия по физике. Ускорение подразумевает наличие отталкивающей силы, которая противодействует гравитации на больших масштабах. Эту силу и назвали тёмной энергией - не потому, что она "тёмная" в буквальном смысле, а потому, что она невидима и неизвестна. В отличие от обычной материи или тёмной материи, которые притягивают, тёмная энергия обладает отрицательным давлением, заставляя пространство расширяться всё быстрее.

Космологическая постоянная: эйнштейновская ошибка или ключ к разгадке?

Самая простая и популярная гипотеза о природе тёмной энергии - это космологическая постоянная, введённая Альбертом Эйнштейном в 1917 году в уравнения Общей теории относительности. Эйнштейн добавил этот член, чтобы сделать Вселенную статичной, как тогда считалось необходимым. Когда Хаббл открыл расширение, Эйнштейн назвал постоянную "своей величайшей ошибкой". Но сегодня она возродилась как возможное объяснение ускорения.

Космологическая постоянная - это постоянная плотность энергии вакуума, присущая самому пространству. Согласно Квантовой теории поля, вакуум не пуст, а полон виртуальных частиц, рождающихся и исчезающих словно из ничего в ничего. Эта вакуумная энергия должна создавать отталкивающую силу, подобную тёмной энергии. Наблюдения сверхновых, показывают, что плотность тёмной энергии соответствует космологической постоянной с высокой точностью.

Но здесь возникает парадокс: теоретические расчёты вакуумной энергии из Квантовой теории поля дают значение, в 10^120 раз больше наблюдаемого. Это одна из самых больших несостыковок в физике, известная как "проблема космологической постоянной".

Почему вакуумная энергия так мала? Это заставляет физиков искать более глубокие объяснения, возможно, связанные с Теорией струн или Антропным принципом, где наша Вселенная "настроена" для существования жизни.

Альтернативные гипотезы

Если тёмная энергия не постоянная, то она может быть динамической. В таком случае она может быть выражена как гипотетическое скалярное поле, подобное полю Хиггса, но с изменяющейся плотностью энергии. Темная энергия могла бы эволюционировать со временем, объясняя, почему ускорение началось относительно недавно - около 5 миллиардов лет назад. Подобные модели предсказывают вариации в уравнении состояния тёмной энергии, которые можно проверить наблюдениями.

Более радикальная гипотеза - гипотеза фантомной энергии - предполагает, что давление здесь ещё более отрицательное, чем у космологической постоянной. Это могло бы привести к "большому разрыву" - сценарию, где расширение становится бесконечным, разрывая галактики, планеты и даже атомы. Хотя фантомная энергия согласуется с некоторыми данными, она вызывает некоторые теоретические проблемы.

Другие концепции предполагают модифицированную гравитацию на больших масштабах или даже то, что наше понимание однородности Вселенной неверно. Но космологическая постоянная остаётся фаворитом благодаря своей простоте и согласию с наблюдениями.

Критика

Тёмная энергия - не бесспорная концепция. Некоторые физики, такие как Субир Саркар, анализируя данные сверхновых, предполагают, что доказательства ускорения слабее, чем считалось, и могут быть артефактами наблюдений.

Альтернативные гипотезы пытаются объяснить имеющиеся данные без тёмной энергии, но они сталкиваются с трудностями в согласовании с реликтовым излучением.

Проблема космологической постоянной - её несоответствие квантовым расчётам - заставляет некоторых ученых сомневаться в текущей модели. Возможно, тёмная энергия - это временная гипотеза, ждущая новой парадигмы, как когда-то эфир уступил место Теории относительности.

* * *

Поиск природы тёмной энергии продолжается. Телескопы картографируют миллиарды галактик, измеряя слабое линзирование и барионные колебания. Проект LSST (Legacy Survey of Space and Time) будет наблюдать сверхновые и переменные звёзды, уточняя уравнение состояния тёмной энергии. Если она динамическая, будущие наблюдения выявят её изменения со временем. Если постоянная - это подтвердит вакуумную энергию, но потребует объяснения её малой величины. Эти усилия не только раскроют тайну ускорения, но и могут привести к новой физике за пределами Стандартной модели.