Алкоголизм и математика не совместимы

#comment_365198522

@Crusad3r, ты в телевизоре

Продолжаем разоблачать лицемерие капитализма по поводу равных возможностей, я докажу что у того кто имеет капитал, возможностей больше с помощью математики.
В прошлом посте Почему бизнес не для бедных #1 или как отсутствие капитала=отсутствие возможностей мы разобрались, что такое математическое ожидание, теперь же мы разберемся, что такое критерий Келли? И почему критерий Келли является причиной того, что капитал даёт возможности эффективным моделям бизнеса?
Критерий Келли это математическая формула, разработанная Джоном Келли в 1956 году. Она помогает определить оптимальный размер ставки (или доли капитала) в рискованных операциях, чтобы максимизировать долгосрочный рост капитала и минимизировать риск разорения. 
Этот критерий объясняет как риск-менеджмент может убить или максимизировать доходность капитала. Вернёмся к орёл и решке.
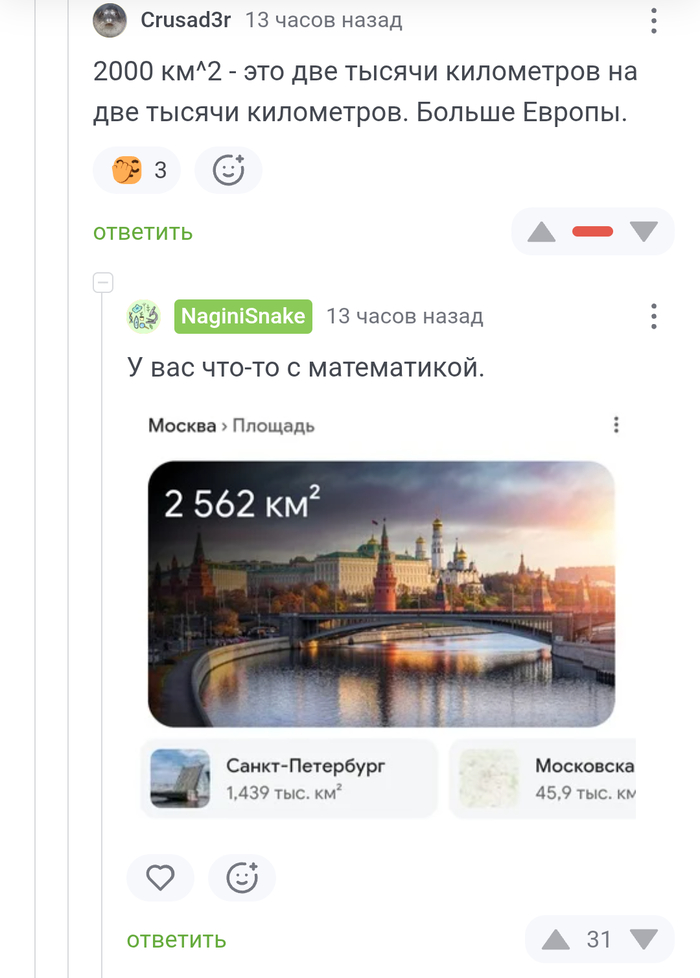
Капитал 100 рублей
Вероятность победы 1/2
коэффициент 3
мат. Ожидание 1,5
и казалось бы, раз ожидание больше единицы, то бизнес модель прибыльная. Однако доходность зависит от риск-менеджмента и сейчас покажу как это работает. При капитале в 100 рублей. Допустим наша стратегия заключается в том, чтобы рисковать 80% капитала каждую ставку. В теории мы никогда не потеряем весь капитал так как если капитал уменьшится то и ставка в 80% от уменьшенного капитала тоже уменьшится, приходим к выводу раз капитал не возможно проиграть полностью, а мат. Ожидание положительное, то и долгосрочная игра также будет положительная. Давайте проверять.
в среднем будет 50% проигрышей и 50% побед. Значит на дистанции количество побед и поражений стремиться к равному количеству.
Так же при победе мы получаем прирост капитала при коэффициенте 3 на 160%(это равнозначно тому что умножить капитал на 2,6), а при поражении убыток в 80%(это равнозначно тому что умножить капитал на 0,2). Теперь составляем равное количество побед и поражений так как вероятность того и другого 50%. Допустим первую игру победили, а вторую игру проиграли. То есть в первую игру мы умножили капитал 100 рублей на 2,6
100*2,6=260 рублей
А вторую игру мы проиграли, умножаем 260 рублей на 0,2
260*0,2=52 рубля
итого при положительном математическом ожидание, но при большом риске наш капитал превратился из 100 рублей в 52 рубля за две игры. То есть даже имея бизнес модель с положительным математическим ожиданием мы всё равно проиграли из-за того, что не рационально рисковали капиталом, брали на себя черезмерный риск, рисковали слишком большой долей капитала и самое главное, слишком сильно отошли от критерия Келли. Критерий Келли при вероятности выигрыша 50% и коэффициенте 3 равен 25%. Да именно 25% капитала на ставку является самым оптимальным для наращивания капитала исходя из условий игры, а точнее при вероятности победы 50% и коэффициенте 3, любое отклонение в + или - от 25% капитала уменьшает потенциальную прибыль или вообще загоняет в убыток предпринимателя. Давайте проверим действительно ли ставка 25% от капитала самый оптимальный вариант? При победе мы умножаем наш капитал на 1,5 при поражении умножаем на 0,75. Первую ставку победили вторую проиграли.
100*1,5=150
150*0,75=112,5
Итого за две игры мы увеличили капитал на 12,5 рублей в отличие от прошлой игры где потеряли 48 рублей.
давайте на всякий случай проверим риск капиталом в 20% сколько в среднем получим за две игры, может 25% это не оптимальный вариант?
победа 1,4 проигрыш 0,8
100*1,4=140
140*0,8=112 рублей, что на 0,5 рублей меньше чем при ставке 25% от капитала
Давайте возьмём 30% от капитала
Победа 1,6 проигрыш 0,7
100*1,6=160
160*0,7=112, что на 0,5 рублей меньше чем при ставке в 25% от капитала.
Теперь при чём же моё утверждение, что капитал=возможность? А дело в том, что если даже у вас есть эффективная бизнес модель с положительным математическим ожиданием, но из-за маленького капитала, придется рисковать большей частью капитала, что просто убьет ваш капитал из-за того что вы не попадёте в критерий Келли. И возможно есть люди с инновационными идеями, но из-за отсутствия капитала их идеи которые могли бы увеличить уровень жизни людей никогда не увидят свет, а если даже эти люди и смогут накопить достаточный капитал для запуска, то просто из-за чрезмерного риска капиталом похоронят достойную идею и свой маленький капитал. Конечно рынок пытается как то с этим работать через инвесторов, которые помогают уменьшить риск, но тут то и начинается лицемерие, когда инвестор обладая лишь капиталом способен заработать деньги на чужой успешной бизнес модели предоставляя возможность обойти критерий Келли бедным и давая возможность инвестору зарабатывать на бизнес модели человека который из-за отсутствия капитала просто не может реализовать свою эффективную бизнес модель, и обязан делиться той прибылью, которую он получил от того что помог обществу своим бизнесом, ведь без инвестора вряд-ли бы он смог реализовать идею. Так что если вы решите основать свой бизнес на все деньги которые у вас есть, то это сродни самоубийству на дистанции, конечно есть исключения, но это единицы, ошибка выжившего. Вот таков лицемерный капитализм который говорит что предоставляет всем равные возможности когда у людей с капиталом возможностей кратно больше.

Другие интересные посты в моем философском учение где я планирую объединять людей ради общих интересов нашей будущей общины https://t.me/Nikudinstvo

Давным-давно мы с одним хорошим преподавателем как-то озадачились, как бы объяснить современным школьникам суть квадратных уравнений на примере параболы.

Немного пошаманили и в итоге получилась игра Космограф:

https://games.pikabu.ru/game/kosmograf

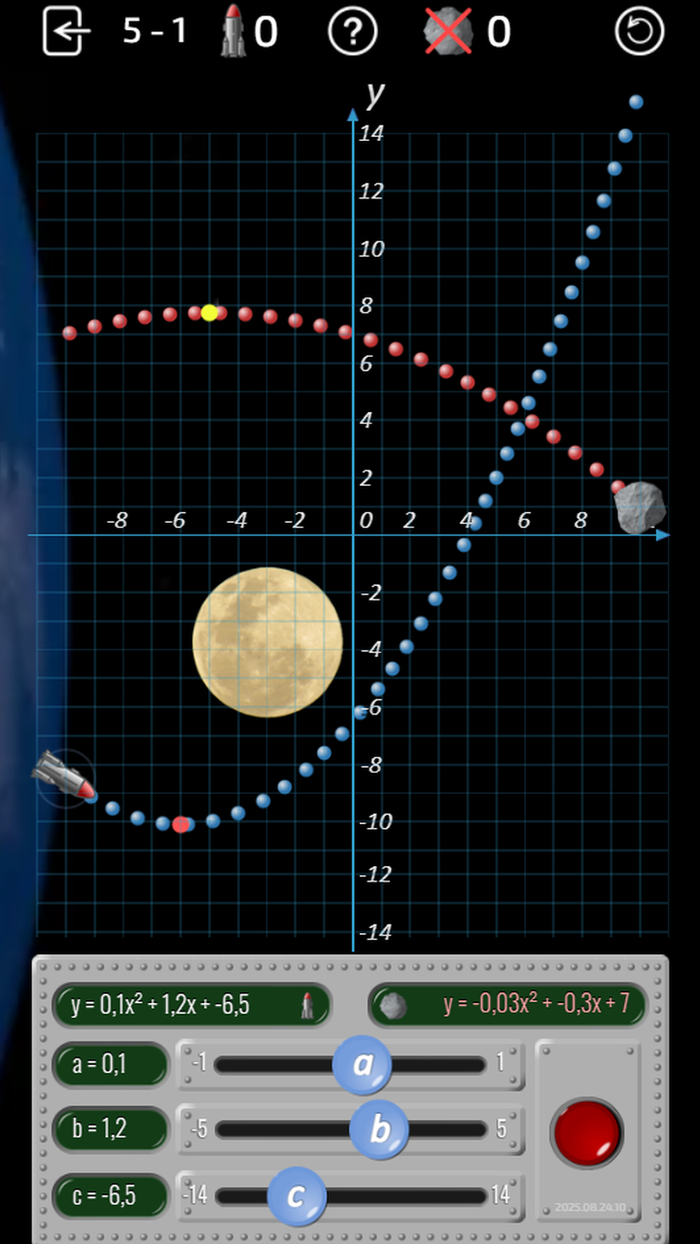
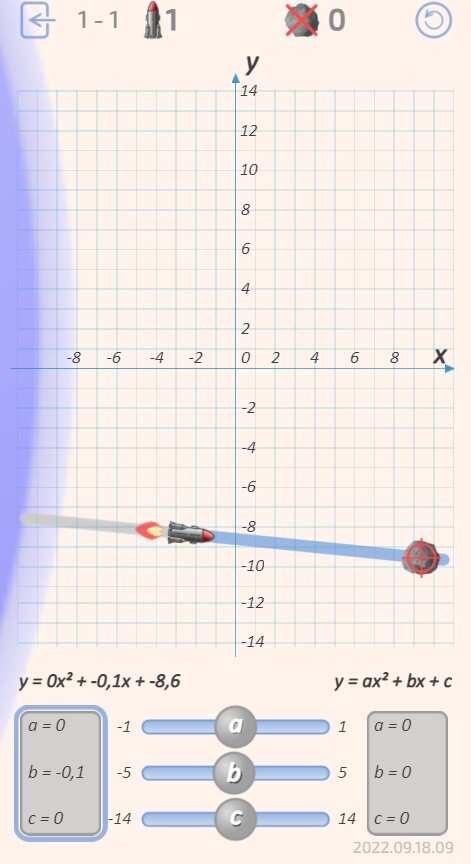
Здесь игроку нужно защитить Землю от астероидов, запуская ракеты по параболическим траекториям.

Как играть

Чтобы нацелить ракету - двигаем синие ручки, отвечающие за параметры параболы.

Затем запускаем ракету красной кнопкой и молимся, чтобы расчёт оказался верным.

Прогрессия

Сначала астероиды прилетают медленно и по прямой линии. Сбивать их достаточно легко.

Затем их орбиты становятся всё более искривлёнными, а скорость повышается.

Следом на пути ракеты появляется Луна.

На последних уровнях мы уже не видим траекторию астероида и можем догадаться о ней только по параметрам уравнения его параболы (красный текст справа над кнопкой).

Теория

В игре есть подробная подсказка, доступная прямо на экране игры.

Вот такая небольшая обучалка у нас получилась.

P.S. В комментариях к самой игре говорят, что вроде она плохо работает на Айфонах. Если что, простите великодушно. Мы люди простые и не имеем в наличии таких аппаратов, чтобы потестировать. :)

P.P.S. К слову, это уже вторая версия Космографа. Первая выглядела попроще.