В дальнейшем, как вы уже поняли, премиум-подписка дорожает день ото дня, вследствие чего Майк много работает и вообще бросается во все тяжкие, просто чтобы оплачивать жизнедеятельность супруги, и в конечном итоге ему приходится её «отключить». Довольно грустная история и вообще, на мой взгляд, одна из лучших серий сезона, демонстрирующая нашу с вами печальную современность. Правда, в нашей реальности по факту всё ЕЩЁ ХУЖЕ. Ведь Майк, хоть и получил грабительскую подписку, по факту изначально не заплатил ни копейки за операцию, спасшую жизнь его жены. В наше же время ты можешь купить машину с автосалона, но при этом оплачивать ежемесячно какую-нибудь функцию вроде подогрева сидений или круиз-контроля. А это уже, на мой взгляд, кидалово настолько высочайшего уровня, что сам Карл Маркс охуел бы от такого антиутопического сценария будущего и подумал бы, что над ним прикалываются. Как можно продать человеку товар и затем требовать с него денег, угрожая отключить через интернет базовые функции УЖЕ ПРОДАННОГО товара? Ведь сюр же, или мне так кажется?

И вот знаете, о чём я подумал при просмотре данной серии? Честно говоря, первой моей мыслью было – а какого хрена Майк не попробовал найти пиратский софт?? Залезь ты, сука, дебил британский, на российский торрент, у нас тут под чёрным флагом есть буквально ВСЁ!!!

Сейчас можете кидаться в меня помидорами, но я не из тех людей, у которых есть аккаунт в Стиме с кучей дорогих игр – все дорогие игры я предпочитаю скачивать бесплатно. И я при этом не испытываю ни капельки угрызений совести по причинам, которые изложу ниже.

Причина первая – я крохобор и нищук.

Причина вторая – огромные бигтехи класть хотели на вас, как на своих пользователей и уж тем более как на живых, чувствующих людей. Вы для них – нули на экранах, цифры, пыль и прибыль. При этом те же медиакорпорации тщательно мониторят пиратские сайты – менеджеры заходят на них, смотрят статистику скачиваний и считают, сколько денег потеряли. После чего идут в суды и засуживают всех подряд – владельцев пиратских сайтов, блогеров, которые борются с pdf-файлами в их же играх (я про Роблокс), хакеров, ломающих DeNuvo…

При этом, стоит вам купить, к примеру, Photoshop, то есть оформить ежемесячную или ежегодную подписку, то мало того, что это крайне неудобно в дальнейшем отменить, то вы в дальнейшем получите ещё и налог за отмену этой самой подписки. Да-да, вы не ослышались – налог за ОТМЕНУ ПОДПИСКИ!

Вдобавок Adobe ещё и внедряет ИИ, который тренируется на людях, создающих собственный контент. То есть ваша интеллектуальная собственность, созданная в купленной вами программе, становится объектом всеобщего достояния и собственностью компании. Когда вы оплачиваете Фотожоб, ваш креатив и ваш контент воруют и скармливают искусственному интеллекту.

Однако если бы вы скачали условный Фотожоб с сайта под пиратским флагом, то вам бы не пришлось заморачиваться на эти темы – что ваше творчество спиздит один из бигтехов, что вам придётся оплачивать налог за отмену подписки раньше срока, ну и заодно вводить все свои данные при регистрации (которые потом как пить дать сольют в даркнет, чтобы вам однажды позвонили из очередной «службы безопасности»).

И это лишь один из примеров. Абсолютно все корпорации занимаются подобным, и абсолютно всем им на вас, как на целевого потребителя, глубоко наплевать. Сначала вам придётся основательно так помучаться при регистрации, а если вы вдруг родом из РФ, то помучаться ещё дольше, а затем вас объегорят и подставят без всяких угрызений совести. Хотите лампово поиграть в GTA4? Пфф, при попытке официального скачивания вам придётся пройти все круги ада, а затем вы получите неиграбельный и неоптимизированный кусок мыла, хотя при этом на торрентах уже лежит абсолютно бесплатно какой-нибудь крутой мод типа Fusion Fix, на который разработчики-Рокстары ещё и подают в суд. Не, я Рокстаров люблю и благодарен им за своё счастливое детство, но ту же ЖТА6 точно не стану покупать за условные 15к, а подожду пару месяцев, пока взломают, и скачаю бесплатно. Думаю, многомиллиардный проект от этого не обеднеет. Тем более, что непонятно, как им сейчас денег занести – тот же Онлайн в RDR2 теперь работает только через три известные всем буквы.

Кстати, причина третья, общечеловеческая. Физические носители исчезают, но как известно, то, что находится в интернете – остаётся в нём навсегда. И пиратский контент – один из немногих способов сохранить эту исчезающую информацию. Которая действительно исчезает и её становится порой невозможно найти даже в мировой сети. Однако даже если исчезнет один из сидеров, раздающих торрент, всегда останется несколько других, и пиратство, по сути, один из немногих способов архивирования новейшей культуры и истории. Если не будет пиратства, то наши потомки, копаясь в сети, никогда не найдут множества вещей, уже сейчас практически исчезнувших безвозвратно. Не только скачивая, но и раздавая информацию, сидер по сути является аналогом переписчика последнего тома канувшей в лету Александрийской библиотеки. Именно этим и важна идея торрента. Это децентрализованный архив информации человечества, который пока что существует, хоть и испытывает давление со стороны медиакорпораций и бигтеха.

Хотя не буду врать. Знаете, я бы доверил бигтеху все свои данные, прошёл сложную систему верификации и даже позволил обучаться на создаваемом мною контенте нейросетям, если бы не…

Если бы не конечная цена продукта. ЖТА6 будет безусловно крутой, и я в неё обязательно поиграю, но сделаю это бесплатно. Спасибо торрентам.

UPD. Всё описанное выше не касается инди-проектов. Их я всецело призываю поддерживать, и здесь торренты можно использовать только для того, чтобы пощупать и потрогать проект, если нет ознакомительного фрагмента, а потом уже приобрести официально. Например, инди-игры я действительно покупаю за деньги.

UPD2. Если вам нравятся мои посты, то подписывайтесь на аккаунт и на моё сообщество в ВК, там ещё больше всякого интересного.

UPD3. Идея для поста и часть информации взята из ролика блогера Фрути Пупс "Пиратство морально оправдано"

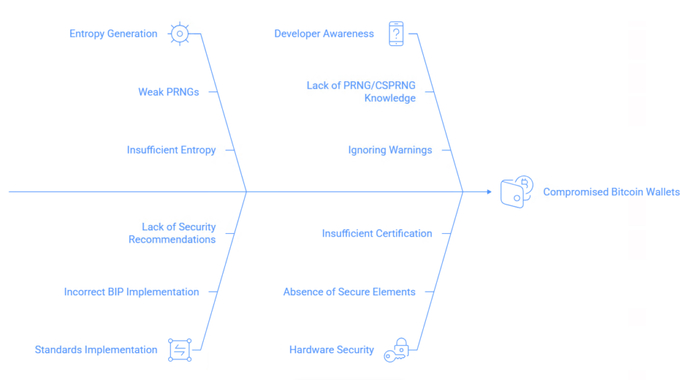
Данная статья представляет комплексный криптоаналитический обзор критической уязвимости CVE-2023-39910, известной под кодовым названием «Milk Sad», обнаруженной в широко распространённой утилите Libbitcoin Explorer версий 3.0.0–3.6.0. Фундаментальный дефект заключается в применении криптографически небезопасного генератора псевдослучайных чисел Mersenne Twister-32 (MT19937), инициализируемого системным временем, что катастрофически ограничивает пространство энтропии до 32 бит вместо требуемых 256 бит. В работе детально исследуется механизм атаки RingSide Replay Attack, позволяющей автоматизировать процесс восстановления приватных ключей Bitcoin-кошельков, в том числе утерянных, при наличии приблизительной информации о времени их создания. Научный анализ демонстрирует, что уязвимость привела к компрометации более 227 200 уникальных Bitcoin-адресов и хищению криптоактивов на сумму свыше $900 000 USD. Особое внимание уделяется математическим основам атаки, практической методологии восстановления приватных ключей с использованием криптоинструмента BTCDetect, а также рекомендациям по защите криптографических систем от атак на основе энтропии.

1. Криптографическая безопасность и парадигма случайности в экосистеме Bitcoin

Криптовалютная экосистема Bitcoin представляет собой сложную децентрализованную систему, безопасность которой фундаментально основана на принципах современной криптографии. Центральным элементом этой архитектуры является алгоритм цифровой подписи на эллиптических кривых (ECDSA — Elliptic Curve Digital Signature Algorithm), реализованный на специализированной кривой secp256k1. Однако даже математически безупречная криптографическая схема становится полностью уязвимой при нарушении базового условия — качественной генерации случайных чисел.

1.1. Теоретические основы криптографической безопасности Bitcoin

Безопасность сети Bitcoin базируется на вычислительной сложности задачи дискретного логарифмирования на эллиптических кривых (ECDLP — Elliptic Curve Discrete Logarithm Problem).

https://dzen.ru/video/watch/69431d5dfd50136dae291001

Приватный ключ k представляет собой случайное 256-битное целое число, которое должно быть:

• Абсолютно непредсказуемым — невозможность угадывания или вычисления

• Уникальным — отсутствие коллизий с другими ключами

• Криптографически стойким — устойчивость к известным атакам

Публичный ключ Q генерируется как точка на эллиптической кривой путём скалярного умножения приватного ключа на генераторную точку G:

Q = k · G

где k — приватный ключ ∈ [1, n-1], G — генераторная точка кривой secp256k1, n — порядок группы

Эллиптическая кривая secp256k1 определяется уравнением Вейерштрасса в сокращённой форме:

y² ≡ x³ + 7 (mod p)

где p = 2^256 − 2^32 − 977 ≈ 1.158 × 10^77

Порядок группы n кривой secp256k1 равен:

n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

n ≈ 1.158 × 10^77

Теоретическая стойкость данной криптосистемы определяется тем, что обратная операция — вычисление приватного ключа k по известному публичному ключу Q — является вычислительно неосуществимой при корректной реализации. Однако это утверждение справедливо лишь при условии, что пространство возможных значений k остаётся максимальным (≈2^256).

1.2. Фундаментальная роль энтропии в криптографических системах

Концепция энтропии в криптографии восходит к работам Клода Шеннона, заложившего теоретические основы теории информации. Энтропия Шеннона определяется как мера неопределённости (случайности) в системе:

H(X) = −Σ p(xᵢ) · log₂ p(xᵢ)

где H(X) — энтропия случайной величины X, p(xᵢ) — вероятность события xᵢ

Для криптографических приложений требуется максимальная энтропия, при которой все возможные значения равновероятны. В случае 256-битного приватного ключа Bitcoin это означает:

Hmax = log₂(2^256) = 256 бит

Критическое значение энтропии заключается в следующем: если генератор случайных чисел (RNG) производит предсказуемые или имеет ограниченное пространство значений выходные данные, то злоумышленник может перебрать все возможные приватные ключи и восстановить криптографические секреты. Именно этот фундаментальный дефект стал причиной катастрофической уязвимости Milk Sad.

Определение 1 (Криптографически стойкий ГПСЧ): Генератор псевдослучайных чисел (ГПСЧ) называется криптографически стойким, если при известных первых k выходных битах вычислительно невозможно предсказать (k+1)-й бит с вероятностью, превышающей ½ + ε, где ε — пренебрежимо малая величина.

1.3. Историческая хронология обнаружения уязвимости

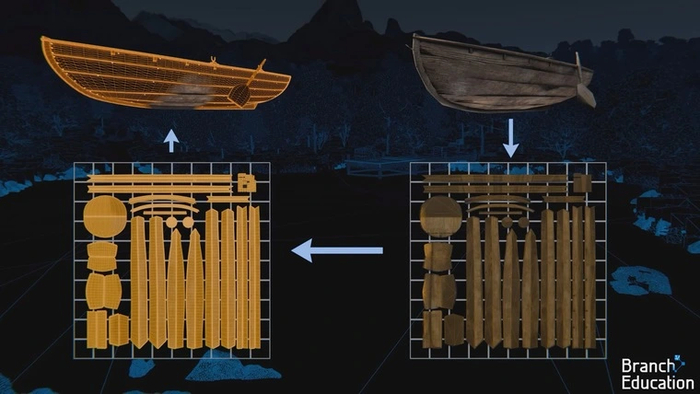
В июне-июле 2023 года исследователи безопасности зафиксировали аномальное явление в блокчейне Bitcoin: множество кошельков, созданных в различные временные периоды, начали систематически опустошаться, несмотря на отсутствие связи между их владельцами. Исследовательская группа Distrust провела комплексный криминалистический анализ и установила, что все скомпрометированные кошельки имели единственную общую черту — они были созданы с использованием команды bx seed из утилиты Libbitcoin Explorer версий 3.x.

Результаты расследования оказались катастрофическими:

ПараметрЗначениеОбщая сумма украденных средств> $900 000 USDЗатронутые криптовалютыBTC, ETH, XRP, DOGE, SOL, LTC, BCH, ZECКомпрометированные Bitcoin-адреса> 227 200Уязвимые версии Libbitcoin Explorer3.0.0 — 3.6.0Период эксплуатацииИюнь — Июль 2023

Кодовое название «Milk Sad» было предложено исследователями как первые два слова мнемонической фразы BIP-39, генерируемой при нулевом начальном значении (seed = 0), что символически отражает «печальное» состояние «молочной» (незрелой, детской) криптографической реализации.

2. Анатомия уязвимости: криптоанализ Mersenne Twister в контексте генерации ключей

2.1. Алгоритм Mersenne Twister: архитектура и криптографические недостатки

Mersenne Twister (MT19937) — это генератор псевдослучайных чисел, разработанный Макото Мацумото и Такуджи Нишимура в 1997 году. Алгоритм основан на линейной рекуррентной последовательности над конечным полем GF(2) и обладает следующими характеристиками:

ПараметрЗначение MT19937Период219937 − 1 (число Мерсенна)Размер слова32 битаРазмер состояния624 × 32 = 19968 битРазмер seed32 битаРавномерность (k-distribution)623-мерно равномерно распределён

Несмотря на превосходные статистические свойства (прохождение тестов Diehard, TestU01), Mersenne Twister категорически НЕ предназначен для криптографических приложений по следующим критическим причинам:

Критические криптографические недостатки MT19937:

• Линейность: Внутреннее состояние может быть полностью восстановлено по 624 последовательным 32-битным выходам

• Ограниченное пространство seed: Только 2^32 ≈ 4.29 × 109 возможных начальных состояний

• Детерминизм: Идентичные seed производят идентичные последовательности

• Предсказуемость: При известном состоянии возможно вычисление всех прошлых и будущих выходов

2.2. Уязвимая реализация в Libbitcoin Explorer

Критическая ошибка в коде Libbitcoin Explorer версий 3.0.0–3.6.0 располагалась в модуле генерации энтропии:

// pseudo_random.cpp (VULNERABLE VERSION) data_chunk random_bytes(size_t length) { std::random_device random; // Getting seed (system time) std::default_random_engine engine(random()); // MT19937 с 32-bit seed std::uniform_int_distribution distribution(0, 255); data_chunk result(length); for (auto& byte : result) byte = distribution(engine); return result; }

При вызове команды bx seed -b 256 | bx mnemonic-new пользователь ожидал получить 256 бит криптографически стойкой энтропии для генерации 24-словной мнемонической фразы BIP-39. Однако реальная картина была катастрофической:

Ожидаемая энтропия: 2^256 ≈ 1.16 × 1077
Фактическая энтропия: 2^32 ≈ 4.29 × 109

Редукция пространства поиска: в 1068 раз

2.3. Математическая формализация атаки

Формализуем уязвимость с использованием строгой математической нотации. Пусть:

• E — энтропия (256 бит), генерируемая для создания кошелька

• S — seed для MT19937, где S ∈ [0, 2^32)

• f(S) — функция генерации последовательности MT19937 из seed S

• trunc32(x) — извлечение первых 32 байт из последовательности

• bip39(E) — преобразование энтропии в мнемоническую фразу

• derive(m) — деривация приватного ключа из мнемоники по BIP-32

• addr(k) — множество Bitcoin-адресов, дериватов приватного ключа k

Определение 2 (Уязвимость Milk Sad):
Существует такой seed S, что:

∃ k, S : trunc32(f(S)) ≡ E (mod 2^256)

такой что

addr(derive(bip39(E))) = Atarget

где Atarget — целевой Bitcoin-адрес.

Вероятность успешного восстановления при полном переборе пространства 2^32:

P(success) = 1 − (1 − 1/N)2^32

где N = 2^160 — общее количество возможных Bitcoin-адресов (P2PKH)

Поскольку 2^32 ≪ 2^160, вероятность ложного совпадения пренебрежимо мала, и при нахождении корректного seed P(success) ≈ 1.

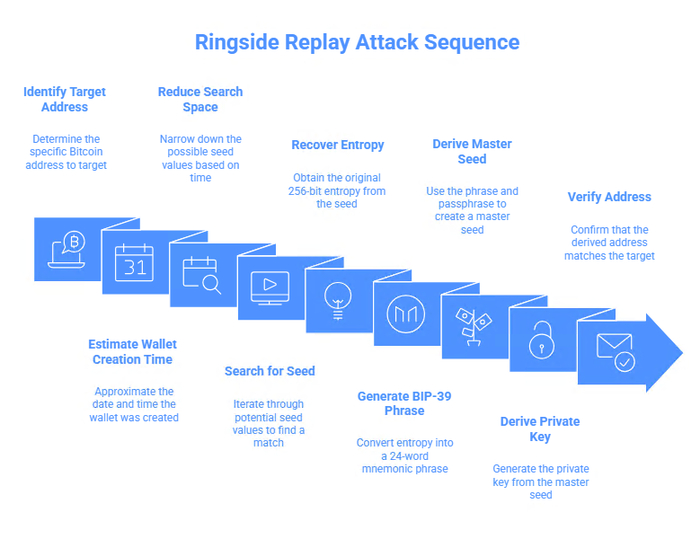
2.4. Детерминированная цепочка преобразований BIP-39/BIP-32

После восстановления исходного 32-битного seed, процесс реконструкции приватного ключа становится полностью детерминированным согласно стандартам BIP-39 и BIP-32:

1. Генерация энтропии: seed → MT19937 → 256-битная псевдослучайная последовательность

2. Вычисление контрольной суммы: SHA-256(entropy) → первые 8 бит

3. Формирование мнемоники: (entropy || checksum) → 24 слова BIP-39

4. Деривация master seed: PBKDF2-HMAC-SHA512(mnemonic, «mnemonic» || passphrase, 2048 итераций) → 512-битный seed

5. Генерация master key: HMAC-SHA512(«Bitcoin seed«, master_seed) → (master_private_key, chain_code)

6. Иерархическая деривация: По пути BIP-44: m/44’/0’/0’/0/0 → конечный приватный ключ

Цепочка преобразований:

S32bit → MT19937 → E256bit → SHA256 → Mnemonic24words → PBKDF2 → Seed512bit → HMAC-SHA512 → (k, c) → BIP-44 → kfinal

3. Эффективность атаки RingSide Replay: вычислительный анализ

3.1. Оценка вычислительной сложности

Полное пространство поиска составляет 232 ≈ 4.29 × 109 возможных значений seed. При известной дате создания кошелька (или приблизительном диапазоне) пространство поиска может быть существенно сокращено:

Сокращение пространства при известной дате:

|Sday| = 86 400 (секунды в сутках)
Редукция: 232 / 86 400 ≈ 49 710 раз

Производительность на современном оборудовании:

ОборудованиеСкорость перебораВремя полного перебора 2^32CPU (Intel i9-13900K)~106 seeds/сек~71 минутаGPU (NVIDIA RTX 4090)~108 seeds/сек~43 секундыFPGA кластер~1010 seeds/сек< 1 секунды

3.2. Количественная оценка эффективности атаки

Эффективность атаки может быть выражена через отношение логарифмов пространств поиска:

Attack Efficiency = log₂(2^32) / log₂(2^256) = 32/256 = 0.125 = 12.5%

Это означает, что пространство поиска сокращается на 87.5% от теоретически безопасного уровня

https://dzen.ru/video/watch/6928c1bb302b5a5c329812fd

Практическое применение: криптоинструмент BTCDetect

Научный анализ использования BTCDetect для восстановления приватных ключей

www.cryptou.ru/btcdetect

BTCDetect представляет собой специализированное программное обеспечение для криптоанализа и восстановления утерянных Bitcoin-кошельков, основанное на выявлении и эксплуатации уязвимостей в криптографических библиотеках. Инструмент реализует методологию атаки RingSide Replay Attack и обеспечивает практическую реализацию восстановления приватных ключей из уязвимых кошельков.

Архитектура BTCDetect

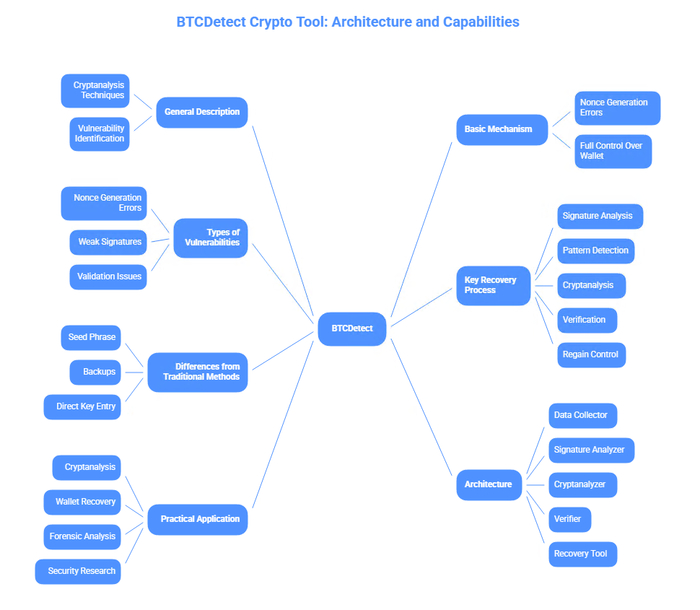
BTCDetect состоит из следующих основных модулей:

• Модуль анализа энтропии: Обнаружение слабых источников случайности в процедурах генерации ключей

• Модуль реконструкции PRNG: Воспроизведение состояния генератора Mersenne Twister по известным параметрам

• Модуль деривации ключей: Реализация полной цепочки BIP-39/BIP-32 для восстановления ключей

• Модуль верификации: Сопоставление восстановленных адресов с целевыми данными блокчейна

Алгоритм работы BTCDetect

Операционная модель BTCDetect включает три основных этапа:

1. Идентификация уязвимых кошельков:

   • Анализ временных меток транзакций

   • Определение вероятного диапазона создания кошелька

   • Идентификация паттернов, характерных для Libbitcoin Explorer

2. Перебор пространства seed:

   • Генерация кандидатов seed на основе временного диапазона

   • Параллельное вычисление цепочек BIP-39 → BIP-32

   • Сравнение полученных адресов с целевыми

3. Верификация и восстановление:

   • Подтверждение корректности восстановленного ключа

   • Проверка валидности подписей

   • Документирование результатов для криминалистического анализа

Практический пример восстановления

Рассмотрим задокументированный случай восстановления приватного ключа:

Bitcoin-адрес 1NiojfedphT6MgMD7UsowNdQmx5JY15djG

Стоимость восстановленных средств $61,025

Восстановленный приватный ключ (HEX)4ACBB2E3CE1EE22224219B71E3B72BF6C8F2C9AA1D992666DBD8B48AA826FF6B

Восстановленный ключ (WIF compressed) Kyj6yvb4oHHDGBW23C8Chzji3zdYQ5QMr8r9zWpGVHdvWuYqCGVU

Публичный ключ (сжатый)

03AE73430C02577F3A7DA6F3EDC51AF4ECBB41962B937DBC2D382CABB11D0D18CE

Валидация восстановленного ключа подтверждает его принадлежность к допустимому диапазону скаляров кривой secp256k1:

1 ≤ k < n

где n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

Научное значение BTCDetect

Методология BTCDetect имеет широкое научное применение, выходящее за рамки конкретной уязвимости Milk Sad:

• Исследование классов PRNG-уязвимостей: Линейные конгруэнтные генераторы (LCG), небезопасные реализации random()

• Криминалистический анализ блокчейна: Выявление паттернов компрометированных кошельков

• Аудит криптографических библиотек: Обнаружение потенциальных уязвимостей до их эксплуатации

• Образовательные цели: Демонстрация критической важности криптографически стойких ГПСЧ

Уязвимость хеш-функции Борромео

Порядок конкатенации данных (R || M || i || j) создаёт потенциальные возможности для атак с расширением длины (length extension attacks) в определённых сценариях.

6.1. Требования к генерации энтропии

Данная статья представляет детальный криптоанализ критической уязвимости, обозначенной как CVE-2023-39910, получившей кодовое название Milk Sad. Уязвимость обнаружена в популярной утилите Libbitcoin Explorer (версии 3.0.0–3.6.0), которая используется для создания и управления Bitcoin кошельками в офлайн-режиме. Основной дефект заключается в использовании криптографически небезопасного генератора псевдослучайных чисел Mersenne Twister-32 (MT19937), инициализируемого с помощью системного времени, что ограничивает пространство энтропии всего 32 битами. Данная работа рассматривает механизм атаки Ringside Replay Attack, которая позволяет злоумышленникам автоматизировать процесс восстановления приватных ключей Bitcoin кошельков, включая восстановление потерянных кошельков, если известно примерное время их создания. Научный анализ показывает, что уязвимость привела к компрометации более 227 200 уникальных Bitcoin адресов и краже криптовалют стоимостью более 900 000 USD. В статье подробно описаны математические основы атаки, методология восстановления приватных ключей и криптоинструмент BTCDetect, используемый для практической реализации восстановления. Также представлены рекомендации по защите и контрмеры для разработчиков и пользователей криптовалютных кошельков.

1. Значение проблемы с валидацией

Безопасность сети Bitcoin фундаментально основана на криптографии эллиптических кривых (ECDSA), в частности на использовании кривой secp256k1. Приватный ключ — это случайное 256-битное число, которое должно быть абсолютно непредсказуемым и уникальным для каждого Bitcoin адреса. Публичный ключ генерируется как точка на эллиптической кривой путём умножения генератора кривой G на приватный ключ:

Q = k · G, where k is the private key

Безопасность этого механизма полностью зависит от качества энтропии, используемой при генерации приватного ключа. Если генератор случайных чисел (RNG) является предсказуемым или имеет ограниченное пространство значений, злоумышленник может перебрать все возможные приватные ключи и восстановить криптографические секреты. Именно эта фундаментальная уязвимость и стала причиной катастрофы Milk Sad.

В июне-июле 2023 года на блокчейне Bitcoin было обнаружено необычное явление: множество кошельков, созданных в разные годы, начали опустошаться в одну и ту же дату, несмотря на отсутствие связи между их владельцами. Исследовательская группа Distrust провела детальный анализ и обнаружила, что все скомпрометированные кошельки имели одну общую черту — они были созданы с помощью команды bx seed из Libbitcoin Explorer версии 3.x.

2. История открытия уязвимости Milk Sad

Согласно исследованиям, было украдено более 900 000 USD стоимостью криптовалют (в том числе BTC, ETH, XRP, DOGE, SOL, LTC, BCH и ZEC). Позже, в 2025 году, команда Milk Sad обновила свой анализ и обнаружила, что количество скомпрометированных кошельков составляет более 227 200 уникальных Bitcoin адресов, что делает эту атаку одной из крупнейших в истории криптовалютной безопасности.

Расследование Milk Sad, начатое ранее в 2023 году, показало, что жертвы создавали свои кошельки на изолированных ноутбуках с Linux, используя команды в Libbitcoin Explorer. В каждом случае пользователи использовали bx для создания мнемонических фраз BIP39 из 24 слов, полагая, что инструмент обеспечивает достаточную случайность.

Одна из команд, использованных при генерации кошелька, выглядела так:

bx seed -b 256 | bx mnemonic-new

Она генерировала 256 бит энтропии, которые затем преобразовывались в мнемоническую фразу из 24 слов. Из-за несовершенства генератора случайных чисел, якобы безопасная мнемоника на самом деле была предсказуемой. Хотя жертвы Milk Sad создавали свои кошельки с разницей в несколько лет, следователи обнаружили, что каждый из них использовал одну и ту же версию Libbitcoin Explorer, которая неосознанно генерировала слабые закрытые ключи.

3. Теоретические основы криптографии Bitcoin и ECDSA

3.1 Кривая secp256k1 и стандарт ECDSA

ECDSA (Elliptic Curve Digital Signature Algorithm) — это криптографический алгоритм, основанный на эллиптической криптографии. В Bitcoin используется специфическая кривая, называемая secp256k1, которая определяется уравнением:

y² ≡ x³ + 7 (mod p) where p = 2^256 − 2^32 − 977

Кривая secp256k1 имеет порядок n ≈ 2^256, что означает, что существует приблизительно 2^256 возможных точек на кривой. Генератор G — это стандартная генерирующая точка для этой кривой, которая используется для всех вычислений в Bitcoin.

3.2 Процесс генерации приватного и публичного ключей

Процесс генерации ключевой пары в Bitcoin выглядит следующим образом:

1. Генерация энтропии: Генерируется 256-битное случайное число, которое служит приватным ключом k. Это число должно быть в диапазоне 1 ≤ k < n, где n — порядок базовой точки.

2. Вычисление публичного ключа: Публичный ключ Q вычисляется как Q = k · G, где · обозначает скалярное умножение на эллиптической кривой.

3. Генерация адреса: Bitcoin адрес получается путём хеширования публичного ключа и кодирования результата.

Критическим моментом является генерация энтропии на шаге 1. Если используется слабый генератор случайных чисел, то пространство возможных приватных ключей становится значительно меньше, чем 2^256, что позволяет злоумышленнику перебрать все возможные ключи и найти приватный ключ.

4. Mersenne Twister-32: архитектура и недостатки

4.1 История и описание алгоритма

Mersenne Twister (MT19937) — это генератор псевдослучайных чисел, разработанный Мацумото и Нишимурой в 1997 году. Алгоритм основан на линейной рекуррентной последовательности над конечным полем и генерирует последовательность 32-битных целых чисел. Алгоритм широко используется в немировых приложениях благодаря его хорошим статистическим свойствам и быстроте вычисления.

Однако Mersenne Twister категорически НЕ предназначен для криптографических приложений по следующим причинам:

1. Предсказуемость: Выходные значения RNG могут быть полностью восстановлены при наличии последовательности из 624 последовательных 32-битных выходов.

2. Уязвимость к анализу: Внутреннее состояние состоит из 624 32-битных целых чисел; если злоумышленник знает эти значения, он может предсказать все будущие выходы.

3. Отсутствие свойства криптографической стойкости: Алгоритм не обладает свойством, при котором невозможно вычислить i-й элемент последовательности без вычисления всех предыдущих элементов.

4.2 Использование Mersenne Twister в Libbitcoin Explorer 3.x

В коде Libbitcoin Explorer 3.x процесс генерации энтропии для создания новых кошельков реализован следующим образом:

Команда bx seed использует эту функцию для генерации начальной энтропии при создании новых Bitcoin кошельков. Вот типичный вызов:

bx seed -b 256 | bx mnemonic-new

Эта команда должна была бы создать 256 бит случайной энтропии, которая затем преобразуется в 24-словную BIP-39 мнемоническую фразу. Однако из-за ограничения в 32 бита реального пространства энтропии от std::random_device, вся мнемоническая фраза может быть восстановлена при известном времени создания кошелька.

5. Математические основы атаки Ringside Replay

5.1 Принцип 1: Ограниченное пространство энтропии

Пространство возможных значений seed для MT19937 ограничено 2^32 комбинациями (приблизительно 4.3 миллиарда возможных значений). Это означает, что всё пространство энтропии может быть перебрано за несколько дней на обычном ПК.

Пространство поиска = 2^32 ≈ 4.29 × 10^9 возможных значений

5.2 Принцип 2: Предсказуемость по времени создания

Если известна дата создания кошелька (или примерный диапазон дат), пространство поиска может быть дополнительно сокращено. Системное время, используемое для инициализации MT19937, может быть восстановлено с высокой вероятностью, если известны:

• Год создания кошелька

• Месяц/день (если известны из истории транзакций)

• Приблизительное время суток

Сокращение пространства поиска до диапазона дат, например за один день, уменьшает количество попыток примерно в 86 400 раз (количество секунд в дне).

5.3 Принцип 3: Детерминированное преобразование в приватный ключ

После восстановления исходной 256-битной энтропии её преобразование в приватный ключ полностью детерминировано согласно стандартам BIP-39 и BIP-32:

1. Энтропия → SHA-256 контрольная сумма → 24-словная BIP-39 фраза

2. BIP-39 фраза + пассфраза → PBKDF2-HMAC-SHA512 (2048 итераций) → 512-битный мастер seed

3. Мастер seed → HMAC-SHA512("Bitcoin seed") → мастер приватный ключ + цепной код

5.4 Формальное математическое определение уязвимости

Пусть:

• E — энтропия, которая должна быть генерирована (256 бит)

• S — seed для MT19937, где S ∈ [0, 2^32)

• f(S) — функция, которая генерирует MT19937 последовательность из seed S

• trunc_32(x) — функция, которая берёт первые 32 байта из последовательности MT19937

• bip39(E) — преобразование энтропии в BIP-39 мнемонику

• derive(m) — преобразование мнемоники в приватный ключ

• addr(k) — множество всех возможных Bitcoin адресов, дериватов из приватного ключа k

Уязвимость определяется как:
∃ k, S : trunc_32(f(S)) ≡ E (mod 256)
такой что addr(derive(bip39(E))) = A_target

где A_target — целевой Bitcoin адрес.

5.5 Вероятность успешного восстановления

При перебор полного пространства 2^32:

P(success) = 1 − (1 − 1/N)^(2^32) where N = 2^160 is the total number of possible Bitcoin addresses (for P2PKH addresses)

Поскольку 2^32 << 2^160, вероятность ложного совпадения ничтожно мала, и P(success) ≈ 1 при нахождении правильного seed.

6. Процесс восстановления приватного ключа

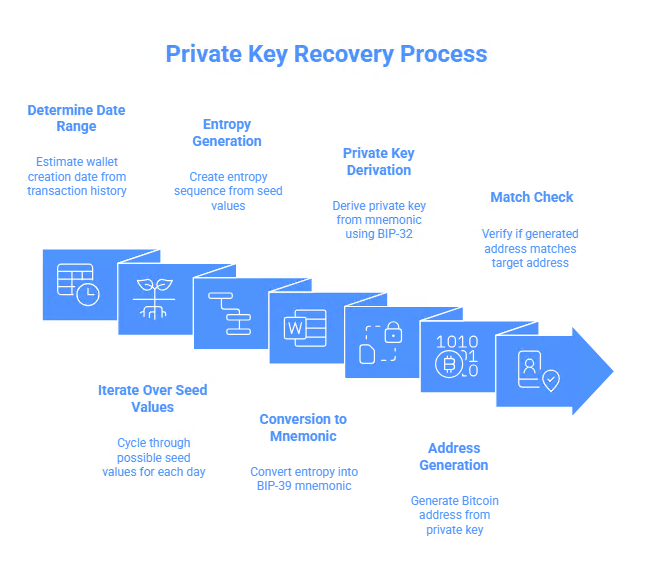
6.1 Алгоритм восстановления ключа

Процесс восстановления приватного ключа для скомпрометированного Bitcoin кошелька состоит из следующих этапов:

1. Определение диапазона дат: Из истории транзакций определяется примерная дата создания кошелька. Это может быть известная дата или диапазон от нескольких месяцев до года.

2. Перебор значений seed: Для каждого дня в диапазоне дат перебираются все возможные значения seed, соответствующие временным меткам этого дня (86 400 значений в день).

3. Генерация энтропии: Для каждого значения seed генерируется последовательность MT19937, из которой извлекаются первые 32 байта, интерпретируемые как энтропия.

4. Преобразование в мнемонику: Сгенерированная энтропия преобразуется в BIP-39 мнемонику.

5. Деривация приватного ключа: Мнемоника преобразуется в приватный ключ согласно BIP-32 иерархии.

6. Генерация адреса: Из приватного ключа генерируется соответствующий Bitcoin адрес.

7. Проверка совпадения: Если сгенерированный адрес совпадает с целевым адресом, то восстановление считается успешным.

6.2 Сложность вычислений

На современном оборудовании (например, GPU NVIDIA RTX 3090):

• Если известна точная дата: примерно 86 400 проверок = несколько минут на одном GPU

• Если известен год: примерно 365 × 86 400 ≈ 31 536 000 проверок = несколько часов на одном GPU

• Если используется полное пространство 2^32: примерно 4 294 967 296 проверок = несколько дней на одном GPU

Данные расчёты показывают, что восстановление приватного ключа практически осуществимо даже для непрофессиональных злоумышленников.

7. Реальный пример: восстановление ключа адреса 1NiojfedphT6MgMD7UsowNdQmx5JY15djG

7.1 Исходные данные компрометации

Рассмотрим задокументированный случай восстановления приватного ключа из Bitcoin-адреса 1NiojfedphT6MgMD7UsowNdQmx5JY15djG:

Bitcoin адрес 1NiojfedphT6MgMD7UsowNdQmx5JY15djG Стоимость восстановленных средств $ 61.025

Восстановленный приватный ключ (HEX) 4ACBB2E3CE1EE22224219B71E3B72BF6C8F2C9AA1D992666DBD8B48AA826FF6B

Восстановленный приватный ключ (WIF compressed) Kyj6yvb4oHHDGBW23C8Chzji3zdYQ5QMr8r9zWpGVHdvWuYqCGVU

Восстановленный приватный ключ (Decimal) 95490713496748161492785334010456634825357659290488148536925849552527657999353

7.2 Валидация ключа в пространстве secp256k1

Приватный ключ k должен удовлетворять ограничению:

1 ≤ k < n where n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141 ≈ 1.158 × 10^77

Результат проверки: ✓ ВАЛИДЕН (ключ находится в допустимом диапазоне скаляров)

7.3 Вычисление публичного ключа и адреса

Восстановленный приватный ключ позволяет вычислить публичный ключ:

Публичный ключ (несжатый, 130 символов) 04BC79D7CC638214D0FE1902A8F3A0EEC3F2B41F5792043559AD6161D23467C234BCD34142146FF3E0DF1648A2B83F392B738AF7598C5B137C2A4500B6E12CECFD Публичный ключ (сжатый, 66 символов) 03AE73430C02577F3A7DA6F3EDC51AF4ECBB41962B937DBC2D382CABB11D0D18CEBitcoin адрес (uncompressed) 1NiojfedphT6MgMD7UsowNdQmx5JY15djG

7.4 Практическое значение восстановленного ключа

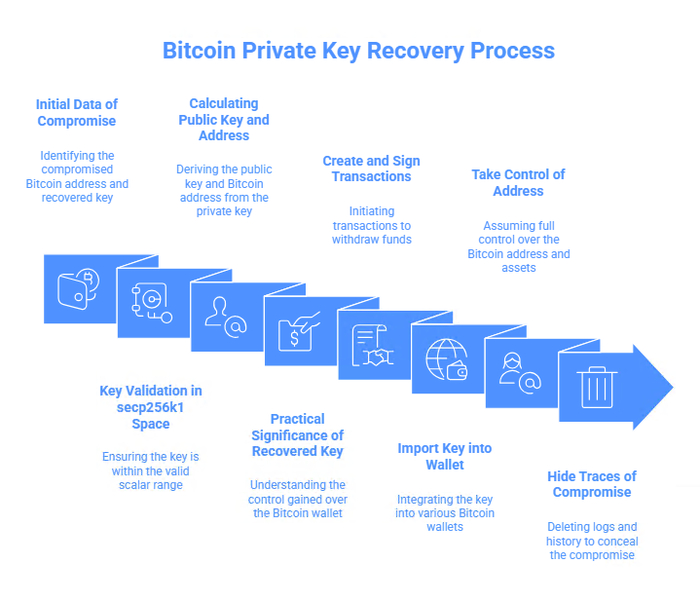
Восстановленный приватный ключ предоставляет полный контроль над Bitcoin-кошельком, позволяя злоумышленнику:

Возможности с восстановленным приватным ключом:

• Создавать и подписывать транзакции для вывода всех средств на контролируемый адрес

• Импортировать ключ в любой Bitcoin кошелек (Electrum, Bitcoin Core, MetaMask и т.д.)

• Полностью захватить контроль над адресом и всеми его активами

• Скрыть следы компрометации путём удаления всех логов и истории

8. Криптоинструмент BTCDetect: архитектура и возможности

8.1 Общее описание BTCDetect

BTCDetect — это программное обеспечение, разработанное для восстановления утерянных биткойн-кошельков путём применения методов криптоанализа и выявления уязвимостей в криптографических библиотеках, таких как SharpECC. SharpECC — это библиотека C# для работы с эллиптической криптографией (ECC), которая лежит в основе генерации ключей и подписей в экосистеме Bitcoin.

Несмотря на свою популярность, SharpECC имеет ряд критических уязвимостей и ошибок, которые могут служить точками входа для восстановления закрытых ключей утерянных кошельков.

Отличие BTCDetect от традиционных методов восстановления

BTCDetect работает на уровне уязвимости криптографической реализации, что отличает его от традиционных методов восстановления:

Seed фраза (BIP-39)24 или 12 слов мнемоники Восстановление всех ключей в иерархии Резервные копии (wallet.dat) Файл wallet.dat Восстановление всех кошельков Прямой ввод ключей Приватный ключ (WIF или HEX)Контроль над конкретным адресом BTCDetect

9. Контрмеры и рекомендации

9.1 Немедленные действия для пострадавших пользователей

⚠️ Для пользователей, которые создали Bitcoin кошельки с использованием Libbitcoin Explorer 3.x:

1. Немедленная миграция средств:

   • Создать новый кошелек с использованием криптографически безопасного метода генерации энтропии

   • Перевести все средства на новый адрес

   • Уничтожить или использовать старый адрес только для мониторинга

2. Проверка компрометации:

   • Использовать инструменты анализа для проверки, не был ли конкретный адрес скомпрометирован

   • Проверить, нет ли неавторизованных транзакций из кошелька

3. Восстановление потерянных средств:

   • Если кошелек был создан в известную дату, можно использовать методы восстановления для получения приватного ключа

   • Перевести восстановленные средства на безопасный кошелек

10. Выводы и перспективы исследований

10.1 Ключевые выводы исследования

Уязвимость CVE-2023-39910 (Milk Sad) демонстрирует критическую важность правильной генерации энтропии в криптографических приложениях. Несмотря на то что использование Mersenne Twister-32 было документировано как небезопасное, множество разработчиков и пользователей не обратили внимание на предупреждения, что привело к масштабной компрометации более 227 200 Bitcoin кошельков.

Итоговое заключение

Криптографические системы и ошибки реализации связаны не с теоретической зрелостью, а с банальными инженерными просчетами. Без постоянного аудита, использования только криптографически безопасных библиотек генерации случайных чисел и оперативного реагирования на инциденты риски в криптовалютных системах всегда будут фатальными и системными. Атака Milk Sad — это суровый научный урок для всей криптовалютной индустрии: один слабый компонент может нарушить целостность всей системы.

References:

1. Polycurve Extraction Attack: A polycurve extraction attack (CVE-2023-39910) leads to private key recovery and theft of Bitcoin funds, where an attacker is able to gain control of BTC funds through a libbitcoin flaw. Polycurve Extraction Attack The core of the libbitcoin crypto library contains a critical vulnerability: an elliptic curve point received from outside the library fails a full mathematical check to determine…Read More

Данный материал создан для портала CRYPTO DEEP TECH для обеспечения финансовой безопасности данных и криптографии на эллиптических кривых secp256k1 против слабых подписей ECDSA в криптовалюте BITCOIN. Создатели программного обеспечения не несут ответственность за использование материалов.

Crypto Tools

Исходный код

Google Colab

Telegram: https://t.me/cryptodeeptech

Видеоматериал: https://youtu.be/KJNbwfolL6g

Video tutorial: https://dzen.ru/video/watch/69431d5dfd50136dae291001

Источник: https://cryptodeeptool.ru/ringside-replay-attack

ГП с трассировкой — устройство и принцип работы

Несмотря на все ухищрения, для быстрых расчетов трассировки все также требуется мощное вычислительное оборудование. Поэтому видеокарты, поддерживающие ее, оснащаются тысячами шейдерных процессоров и специализированными вычислительными блоками — RT-ядрами.

Шейдерные процессоры выполняют арифметические операции, в то время как RT-ядра разработаны и оптимизированы именно для операций трассировки лучей.

Внутри RT-ядер находится два вычислительных движка. Первым начинает работу движок, занимающийся поиском пересечений лучей с объемами-коробками BVH.

Когда находится самая маленькая коробочка, пересекающая луч, в дело вступает второй движок. Он ищет пересечения лучей с полигонами.

Как и шейдерные процессоры, RT-ядра работают параллельно друг с другом. На современных видеокартах это позволяет обрабатывать несколько миллиардов лучей в секунду, а общий счет выполненных операций при этом достигает триллионов. Например, NVIDIA GeForce RTX 3090 родом из 2022 года выполняет за одну секунду до 36 триллионов операций. Тогда как самый мощный суперкомпьютер 2000 года, полагающийся на грубую вычислительную мощность центральных процессоров, за то же время осуществлял лишь 12,3 триллиона.

Чем отличается трассировка лучей

Трассировка пути — наиболее продвинутый способ получения компьютерных изображений. Но из-за ее высоких требований в играх пока более распространена обычная трассировка лучей. Оба способа имеют схожую основу, но трассировка лучей обеспечивает меньшую реалистичность освещения взамен на гораздо более скромные требования к оборудованию.

Для реализации трассировки лучей существует несколько техник. Рассмотрим две самые распространенные. Первый вариант схож с трассировкой пути, но имеет некоторые упрощения. Сначала для моделей сцены создаются дубликаты низкого разрешения с малым количеством полигонов.

Кадр с этими моделями просчитывается вне экрана, чтобы получить карту освещенности поверхностей. А затем полученная карта накладывается на кадр высокого разрешения, выводимый на экран.

Это позволяет хорошо интерполировать непрямое освещение, не прибегая к огромному количеству вычислений. Данный способ является одним из методов трассировки, который используется системой освещения Lumen в графическом движке Unreal Engine 5. Второй вариант техники называется трассировкой лучей в экранном пространстве. Тут используется совершенно другой подход на основе трех составляющих: изображения, полученного с помощью традиционного рендеринга, карты глубины кадра и карты нормалей. Из отрендеренного изображения берется информация о цвете объектов. Карта глубины показывает, насколько далеко они находятся от камеры.

В свою очередь, карта нормалей сообщает, в какую сторону полигоны отражают свет.

Когда в процессе трассировки луч попадает на отражающую поверхность, его дальнейшее распространение продолжается в соответствии с этой информацией. Например, попав в озеро, лучи отразились в сторону деревьев — значит на поверхности озера появится искаженное изображение последних.

Главная проблема подобного подхода в том, что он может использовать только отрендеренные кадры с экрана. То есть, когда деревья исчезнут из поля зрения игрока, пропадет и их отражение в озере. Такую технику трассировки лучей используют многие игры прошлых лет, в том числе — Cyberpunk 2077.

Трассировка пути — продвинутая технология построения изображений в компьютерной графике. Она широко применяется для создания реалистичных сцен в фильмах, и все больше становится популярной в новых играх для ПК и консолей. Как работает эта технология, и в чем ее отличия от более распространенной трассировки лучей?

Что такое трассировка пути

Компьютерная графика, используемая в современном кинематографе, основана на одной из техник трассировки лучей — трассировке пути (Path Tracing). Этот алгоритм появился в далеком 1986 году, но из-за своей сложности лишь спустя 30 лет начал массово использоваться для создания графики в фильмах.

Чтобы понять, почему все это время трассировка пути оставалась неосуществимой, ознакомимся с основами построения подобной картинки. Сначала 3D-художники вручную моделируют форму объектов в сцене, а программное обеспечение для рендера разбивает их на мелкие треугольники — полигоны.

Затем на модели накладываются текстуры, которые симулируют материалы определенного цвета и типа — например, шероховатые, гладкие или стеклянные.

Готовые объекты и источники света: солнце, небо, фонари, размещаются в нужных положениях на 3D-сцене. После этого добавляется виртуальная камера и запускается процесс рендеринга — благодаря ему картинка в кадре визуализируется в виде привычного 2D-изображения.

С помощью трассировки пути имитируются отражения света от различных материалов. К примеру, попав на матовую красную черепицу крыши, часть света ей будет поглощена, а другая часть — отразится красным. Отраженный свет от каждого объекта попадает в виртуальную камеру, внося свой вклад в создание изображения.

Для образования каждой точки конечной картинки осуществляется несколько тысяч подобных расчетов. А для формирования одного кадра изображения с разрешением 4К их потребуется несколько миллиардов.

Именно из-за этого долгое время создание изображений с использованием трассировки пути было очень медленным процессом. Например, в 2016 году рендерингом фильмов «Зверополис» и «Моана» занималась ферма из тысяч серверов, которые производили вычисления в течении нескольких месяцев — и это всего для двух часов анимации.

Формирование изображения

Для начала ознакомимся с принципом создания изображения при трассировке пути. Этот алгоритм относится к виду вычислений, которые очень хорошо распараллеливаются: точки картинки независимы друг от друга, поэтому тысячи лучей для каждой из них можно рассчитывать одновременно.

Если показать на картинке траектории всех лучей, которые просчитываются для этой сцены, то она заполнится огромным количеством линий. Поэтому рассмотрим данный процесс на примере одной точки. Первый луч испускается из ее центра и попадает на полигон какого-либо объекта в кадре.

Базовый цвет точки формируется с помощью нескольких лучей, которые попадают рядом с центральным — для этого все их цвета усредняются. Подобные лучи называются первичными.

В результате такого подхода формируется изображение с правильной перспективой.

Глобальное освещение

Мы рассмотрели, как цвет полигонов передается точкам виртуального кадра. Но для получения реалистичной сцены нужно просчитать глобальное освещение объектов — ведь яркость и оттенок цвета каждой точки зависит именно от него.

Для этой цели комбинируются два вида расчетов: прямого (Direct) и непрямого (Indirect) освещения. При первом виде вычислений просчитываются лучи непосредственно от источников освещения — солнца, неба и ламп. Они называются теневыми.

Теневые лучи отражаются от всех объектов сцены, попутно приобретая характер и окраску от их материалов. Таким образом все поверхности, на которые попадает прямое освещение, становятся источниками непрямого. Отраженный свет проникает во все области кадра. В том числе в те, которые закрыты преградами от лучей прямого освещения. На примере ниже можно увидеть, как освещенная зеленая точка на стене отражает свой свет на синюю точку столба, находящуюся в тени.

Этот луч, проходящий между двумя точками, называют вторичным. Если при первом отражении он снова попадет в тень, то от него будут просчитаны дополнительные лучи. Так будет продолжаться либо до попадания на освещенную прямым светом точку, либо до достижения лимита отскоков, при котором дальнейший поиск траектории луча прекращается.

Вместе с траекториями лучей от источников прямого освещения это создает большое количество вычислений. Например, в кадре ниже для получения 20 первичных лучей необходимо рассчитать почти сотню вторичных и теневых.

Благодаря непрямому освещению реалистично просчитывается не только изменение яркости точек, но и их взаимное влияние на цвет друг друга. К примеру, если расположить рядом со столбом красный воздушный шар, то за счет непрямого освещения в его оттенок окрасится и тень от столба.

Не менее важно и то, что направление распространения вторичных лучей зависит от свойств материала объекта. Если он идеально гладкий, то угол падения луча будет равен углу его отражения — благодаря этому поверхность будет выглядеть зеркальной. А от шероховатого материала того же цвета лучи будут отражаться в случайные стороны — из-за этого он, как и положено, будет отображаться матовым.

В случае, если материалом выступает стекло, то будет просчитываться не только отражение света, но еще и его преломление при прохождении насквозь.

Сложность трассировки пути зависит от количества источников света, количества лучей на точку и предельно допустимого числа их дополнительных отскоков. У сцены из первого примера с замком используется четыре источника света, тысяча лучей на точку и 12 отскоков. Чтобы визуализировать один ее кадр в 4К, нужно просчитать примерно 400 миллиардов лучей.

А для создания всего одной секунды такого видео их понадобится просчитать уже около триллиона. Именно поэтому в течение нескольких десятилетий трассировка пути для фильмов считалась невозможной.

Чтобы достичь приемлемой производительности, в современных играх трассировка пути реализована намного проще — один-два луча на точку и от одного до четырех отскоков. Но даже при таких параметрах и базовом разрешении Full HD для комфортной игры каждую секунду видеокарте понадобится просчитывать около полумиллиарда лучей.

Иерархия ограничивающих объемов

Еще одна ключевая трудность при трассировке пути — узнать, на какой именно полигон луч из точки попадает первым, чтобы определить ее основной цвет. В случае, если полигонов десятки или сотни, можно воспользоваться вычислением траектории луча с помощью математических уравнений. Но в современных сценах их миллионы, поэтому этот способ потребует огромных вычислительных ресурсов. Чтобы упростить данный процесс, используется иерархия ограничивающих объемов (Bounding Volume Hierarchy, BVH). При таком подходе сцена разделяется на виртуальные объемы-коробки, в каждой из которых оказывается одинаковое количество полигонов.

Коробки делятся надвое до тех пор, пока в каждой из них не останется всего несколько полигонов (обычно от 4 до 32). В нашем примере сцена состоит из трех миллионов полигонов, которые «раскладываются» в полмиллиона небольших коробочек.

Положение каждой коробки в пространстве выровнено строго по осям координат. Когда луч начинает свое путешествие из точки, его направление сравнивается с координатами первой пары больших коробок. Коробка, которую он не пересекает, исключается из расчетов — как и все более мелкие, на которые она поделена.

Затем направление луча сравнивается с координатами двух меньших коробок, на которые разделена исходная. И так до тех пор, пока луч не достигнет самой маленькой коробки.

В виду ограничения фотоматериалов

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...

В целом, модельки можно починить в Meshmixer, использовать их, как основу для дальнейшего улучшения, придания нужного вида.

Прошедшие пару недель ознаменовались очередным расширением списка дырищ в экосистеме Linux.
Согласно мнению некоторых персонажей, в опенсорсе присутствуют волшебные бесплатные фиксики, поэтому, если в опенсорсе и есть какие-то баги, живущие там десятилетиями, то это пропаганда Microsoft, Oracle, IBM (все трое – крупнейшие из разработчиков Opensource\Linux, IBM с недавних пор – владелец Red Hat).

В реальности

В одной из вариаций на тему Git – Gogs, еще 23 декабря 2024, год назад, нашли дыру с дверь ангара для Боинга: CVE-2024-55947
Спустя год оказалось, что дыру не закрыли, а кое-как залатали досками, и теперь владельцев сервиса, злые люди активно пользуют в ту же самую дыру, только с другим названием - CVE-2025-8110. Новость в мире появилась еще вчера на  theregister (Wed 10 Dec 2025 // 21:31 UTC), сегодня ее потащили по новостным каналам.

В Tika (сервис по определению типа файла и его метаданных)
20 августа 2025 в нем нашли дыру на 10 из 10 - CVE-2025-54988. Вроде кое-как заколотили досками, но – 4.12.2025 ни разу не было и вот опять, CVE-2025-66516.

Что тут сказать? Полгода-год, на повторную дыру, это еще быстро. Серьезные дыры в базовых сервисах Linux существуют годами, как Heartbleed (CVE-2014-0160) и SambaCry (CVE-2017-7494), а просто кривой код на уровне ядра, типа проблемы планировщика Completely Fair Scheduling (CFS) может быть и лет 10, может и больше, начиная с kernel 2.6.38+ и далее.

На фоне таких новостей очень интересно читать рассекреченные документы АНБ – и про то, что Windows стал очень плохо взламываться, и про то, что в сообщество Linux разработки вполне удается проносить специально ослабленный код, как было с Dual_EC_DRBG (Dual Elliptic Curve Deterministic Random Bit Generator), и не только:

Команда специалистов по кибербезопасности из китайской Pangu Lab опубликовала отчет, посвященный бэкдору Bvp47, работающему в операционных системах семейства Linux. Программу связывают с хакерской группировкой (APT) Equation Group, которая, по данным аналитиков, действует в интересах Агентства национальной безопасности (АНБ) США.
В ОС Linux 10 лет работает «жучок» АНБ США, следящий за «военкой» и телекомом по всему миру

Очень мне в свое время понравился метод - Обход шифрования диска в Linux через непрерывное нажатие клавиши Enter.

Заключение

Тут должна быть умная мысль, но мне недавно люди, не отличающие vi от chown, популярно пояснили, что перевод бабушек через дорогу, и почты из Microsoft Exchange в PostgreSQL (PostgreSQL Global Development Group,  Regents of the University of California) – это успешный успех импортозамещения.

Все идет по прежнему ..

Замена американской ОС Windows на американскую ОС на базе linux называется “импортозамещением”.
Шпаргалка по общению с СПО-сектантами

Есть во всем происходящем какая-то сложно уловимая ирония.
Но я подумаю про нее завтра – у меня до сих пор не получается собрать на орбите транспорт до Мюн. Мне до КР-700 (Кербинская ракета - 700) еще как .. Впрочем, сравнение придумайте сами.

Хорошо хоть с понедельника у основных заказчиков приостановка работ, в связи с близким рождеством. Можно будет не выкатывать и откатывать до ночи, но спокойно собрать ракету и написать документацию.

HO. HO. HO. Happy Hogswatch!

PS. Прошу при комментариях не забывать про новую классику, в том числе "я сама дочь офицера разработчик программист и не все так однозначно" и классику, не устаревшую за 100 лет:

1. Despicere (смотреть свысока - лат.), или прием первый.
Состоит  в  том,  что  участник  диспута  должен  дать  почувствовать противнику свое интеллектуальное  и моральное  превосходство, иными словами, дать  понять, что противник  -  человек ограниченный, слабоумный,  графоман, болтун,  совершенный нуль, дутая  величина, эпигон,  безграмотный  мошенник, лапоть,  плевел, подонок и  вообще субъект, недостойный того,  чтобы  с  ним разговаривали. Такая априорная  посылка дает вам затем право на тот барский, высокомерно-поучающий  и  самоуверенный тон,  который неотделим  от  понятия "дискуссия". Полемизировать,  осуждать  кого-то, не соглашаться  и сохранять при этом известное  уважение к противнику - все это не входит в национальные традиции.
Карел Чапек. Двенадцать приемов литературной полемики или Пособие по газетным дискуссиям

Если кто хочет комментировать, а вот беда - не может, то он всегда может написать опровержение, и даже написать его на сайте новостей Минцифры. Там сейчас вообще что угодно можно писать, и про живую воду, и про Эльбрус-128к.
Я такое провержение даже, наверное, прочитаю, если пришлют. Но это не точно.