Нельзя поднять ставку. В рулетке ты можешь поставить на одну ставку всю свою зарплату и шансы проиграть будут чуть больше, чем выиграть. А в лотерее, ты проиграешь, если не случится чудо. Потому что 100 билетов - это не повышение ставки, это её размазывание.

Лотерея - безопасный загон для азарта. Потерять 500 рублей от тысячи в "плохой" лотерее - это как удар игрушечным мечом. А в казино он настоящий и поэтому очень опасный.

А если хочешь рискнуть, полагайся на закономерности, а не на удачу. Иди учиться, осваивай новый навык, вкладывай в себя, займись фрилансом. Джек-пот не гарантируется, но результат зависит от тебя.

А лотерея? Купи один билет, помечтай и живи дальше (или не покупай). В этом и есть её главная польза.

P.S. Для тех кто хочет посмотреть цифры ссылка ниже
https://www.stoloto.ru/ruslotto/archive/1707?draw=1708

2. Объекты и типы: что именно считается «данным»

Я фиксирую объекты теории на уровне, где ещё нет «3D-мира как вещи в себе», но уже есть вычислимая структура.

2.1. Полярности L4

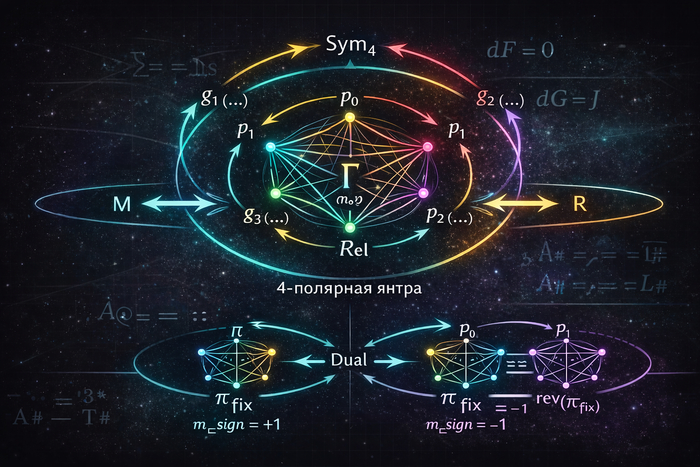
• Полярности янтры L4: P = {p0, p1, p2, p3}.

• Симметрии перестановок/отражений: действие Sym4 на полярностях и построенных отношениях.

2.2. Ветвь ориентации и закон знака

• Есть фиксированная ветвь pi_fix.

• Есть инволюция ветви rev(pi_fix).

• Есть знаковая функция m_sign(pi_fix) ∈ {+1, -1}.

• Ветвевой закон (не обсуждается, а принимается как жёсткий протокол):A0: rev(pi_fix) => m_sign := -m_sign

Это запрещает «подгонку знаков» через неявный выбор правой/левой тройки.

2.3. Типизация M/R Я развожу два типа (два сектора):

• Type = {M, R}

• Дуальность типов:Dual: M <-> R Dual(Dual(x)) = x

Смысл: я запрещаю неявное смешение того, что потом в L2-распаковке станет (условно) электрическим/магнитным и их дуальностью. Любое «перепутали местами» обязано быть явным и пройти контроль.

3. Минимальная локальность: почему появляется оператор d и почему d∘d = 0 не обсуждается

Как только я говорю «контур», «граница», «обход», я уже обязан заплатить логическую цену: появится носитель локальности и оператор границы/дифференцирования.

Я фиксирую носитель локальности как клеточный/цепной комплекс (дискретный вариант) или как его гладкий аналог (формы). Для строгости в инженерном смысле достаточно дискретного описания.

3.1. Цепные группы

• C0 — 0-клетки (узлы)

• C1 — 1-клетки (рёбра)

• C2 — 2-клетки (грани)

• C3 — 3-клетки (объёмы), если нужно

3.2. Операторы границы

d0: C0 -> C1 d1: C1 -> C2 d2: C2 -> C3

3.3. Главная структурная аксиома

A6: d1 o d0 = 0, d2 o d1 = 0

Это не «физика». Это определение того, что значит граница. Граница границы равна нулю. Любая теория, в которой это не так, перестаёт говорить про контуры и локальность и начинает говорить про произвольные символы.

4. Дуальность * и рождение «вихря» как протокола

Чтобы из «границы» получить «вихрь», мне нужна дуальность, которая связывает разные ранги и типы, и при этом контролируется ветвью.

4.1. Ветвезависимая дуальность Я ввожу оператор:

*_{pi_fix}: Ck -> C(3-k) (в 3D-носителе)

и требую ветвевой закон дуальности:

A7: *_{rev(pi_fix)} = m_sign(pi_fix) *_{pi_fix}

4.2. Вихрь как определение Я определяю вихрь не как картинку, а как оператор:

Gamma_{pi_fix} := *_{pi_fix} o d

Именно эта дефиниция заменяет учебниковый «curl» и выносит знак из тени: при rev(pi_fix) знак вихря меняется строго контролируемо через m_sign.

5. Канонические уравнения поля в корневой форме: dF = 0 и dG = J

Теперь я ввожу минимальный набор полевых объектов (без «материальных законов» и без выбора единиц).

5.1. Поле Я рассматриваю:

• F — полевой объект (типизированный, допустимый для применения d)

• G — дуальный полевой объект (через Dual и/или *_{pi_fix})

• J — источник (заряд/ток в общей форме)

Корневой канон:

(1) dF = 0 (2) dG = J

И сразу структурное следствие из A6:

dJ = d(dG) = 0

Закон сохранения источника здесь не «добавляется», а вынуждается структурой.

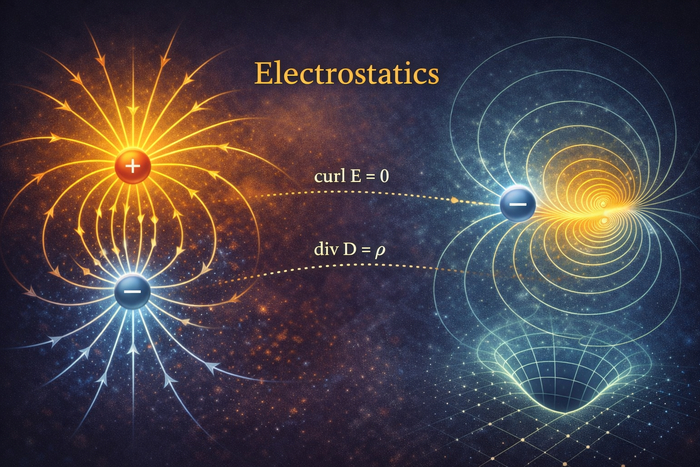
6. Что такое «электростатика» в моём протоколе

Теперь я строго фиксирую статический режим как ограничение на допустимый класс процессов (это важно: «статичность» — часть класса теорий).

Я задаю электростатику как режим, где:

• нет временной эволюции наблюдаемых полей (∂/∂t = 0 в L2-проекции);

• нет токов проводимости в рассматриваемой постановке (J_vec = 0 в L2-проекции);

• остаётся только плотность источника rho (заряд), причём закон сохранения становится тривиальным (∂t rho = 0).

Важно: на корневом уровне я не использую t как фундаментальную координату. «Статический режим» — это условие на проекцию/пайплайн вывода сцены и на допустимые источники, а не утверждение про «время как субстанцию».

7. Гейты электростатики: что должно ловить ошибки (до текста и до «физики»)

Чтобы электростатика была воспроизводимой и не скатывалась в соглашения, я фиксирую минимальный набор QA-гейтов.

ES-G1. Гейт комплекса Проверяет d o d = 0 (в дискретной форме — нулевое произведение матриц инцидентности).

ES-G2. Гейт ветви/знака Проверяет:

*_{rev(pi_fix)} = m_sign *_{pi_fix} => Gamma_{rev(pi_fix)} = m_sign * Gamma_{pi_fix}

ES-G3. Гейт типизации M/R Запрещает смешение типов: Dual и * применимы только там, где это разрешено спецификацией.

ES-G4. Гейт запрета скрытого join Любое «склеивание» идентичностей/узлов/границ обязано быть явным:

• есть join_stage

• есть join_id иначе это автоматически ошибка (особенно важно для odd-слоёв, но в статике тоже критично: иначе легко «подогнать» поле под заряд).

ES-G5. Гейт источника Проверяет, что из dG = J следует dJ = 0 и что статический класс источников не нарушает это.

8. Промежуточный итог: что уже неизбежно, а чего ещё нет

В конце главы 1 я фиксирую честную границу результата.

Уже неизбежно:

• существует локальный оператор d с d o d = 0;

• существует ветвезависимая дуальность *_{pi_fix} со строгим законом знака;

• вихрь Gamma_{pi_fix} определён как * o d;

• канон имеет форму dF = 0, dG = J, и автоматически dJ = 0;

• статический режим — это ограничение на класс процессов/источников.

Ещё не сделано (и будет сделано в Главе 2):

• L2-проекция и строгая распаковка корневых формул в привычные уравнения электростатики;

• вывод именно двух школьных форм: curl E = 0 div D = rho в моей дисциплине ветви/знака и без скрытых соглашений.

Глава 2. Строгая L2-проекция в статике: как из dF = 0 и dG = J неизбежно получаются curl E = 0 и div D = rho

1. Что именно я называю «L2-проекцией» и почему она нужна

На уровне L4 я работаю с типизированными объектами F, G, J и операторами d, *_{pi_fix}, Dual, где знаки контролируются ветвью pi_fix и законом rev(pi_fix) => m_sign := -m_sign.

Но электростатика как инженерный язык живёт в L2 (двухполярности): там есть векторные поля и их производные (div, curl) плюс плотность заряда rho. Чтобы получить эти формы, я обязан ввести операцию проекции:

• выбрать представление наблюдаемого слоя (условно: «пространственный срез»),

• разложить корневые объекты на L2-компоненты,

• определить div и curl не как первичные символы, а как композиции через d и *_{pi_fix}.

Иначе я неизбежно скатываюсь в учебниковое «договорились о знаках».

2. Статический режим как ограничение L2-проекции

В электростатике я фиксирую два условия (как ограничение класса процессов, а не как «физическую веру»):

ES-1 (нет временной динамики L2):

∂/∂t = 0

ES-2 (нет токов в рассматриваемой постановке):

J_vec = 0

Остаётся только плотность rho (источник в статике):

J -> rho

Смысл: во второй корневой формуле dG = J правая часть в статике сводится к «чистому заряду».

3. Как я развожу ранги и компоненты в статике без “3+1” риторики

Чтобы не запутывать читателя лишними конструкциями времени, я делаю минимально необходимое:

• беру 3D-носитель локальности (клеточный комплекс или непрерывный аналог) для L2-описания;

• использую цепи/коцепи соответствующих рангов;

• фиксирую, какие величины относятся к 1-цепям, 2-цепям и 3-цепям.

В дискретной записи это стандартно:

• 1-цепи (C1) — «рёберные» величины (интеграл по ребру);

• 2-цепи (C2) — «гранные» величины (поток через грань);

• 3-цепи (C3) — «объёмные» величины (заряд в ячейке).

Это не «геометрия ради геометрии»; это минимальный носитель, где вообще имеет смысл говорить «граница» и «обход».

4. Определения L2-операторов curl и div как композиций (а не как постулатов)

Теперь — ключевой технический узел: я определяю L2-операторы через d и *_{pi_fix}.

4.1. Вихрь/ротор как оператор

На соответствующем ранге я определяю:

curl_{pi_fix} := *_{pi_fix} o d

Это ровно мой вихрь Gamma_{pi_fix} из Главы 1, просто в L2-языке.

4.2. Дивергенция как дуальная композиция

В дискретной/форменной логике дивергенция — это «дуальный» оператор:

div_{pi_fix} := *_{pi_fix} o d o *_{pi_fix}

(на согласованном ранге; смысл — «взял поток, перешёл дуальностью в рёберное/скалярное, применил d и вернул»).

4.3. Ветвевой контроль знака для curl и div

Из аксиомы:

*_{rev(pi_fix)} = m_sign *_{pi_fix}

следует, что любая формула с curl_{pi_fix} и div_{pi_fix} имеет детерминированное поведение при смене ветви. Это то место, где в обычной записи учебник молчит и прячет знак в «правиле правой руки».

5. Вывод первого уравнения электростатики: curl E = 0

Теперь я показываю, где именно «сидит» электростатический E.

5.1. Где живёт E

В статике электрическое поле естественно живёт как 1-форма (рёберная величина):

• дискретно: интеграл E по ребру;

• непрерывно: 1-форма E.

Поэтому для него корректен оператор d (дающий 2-форму) и далее * (дающий соответствующий вихрь).

5.2. Структурная половина Максвелла и её статическая распаковка

Из корневого тождества:

dF = 0

в статике остаётся та часть, которая относится к «электрическому» компоненту F. Формально: при L2-проекции я получаю закрытость соответствующей компоненты.

В простейшем статическом режиме это даёт:

dE = 0

и, применяя определение curl_{pi_fix} := *_{pi_fix} o d, я получаю:

curl_{pi_fix}(E) = *_{pi_fix}(dE) = 0

То есть первое уравнение электростатики возникает как логическое следствие:

• корневого тождества dF = 0,

• того, что curl определён как * o d,

• и того, что статический режим исключает временные компоненты.

В школьной записи это:

curl E = 0

5.3. Никакой «подгонки» знака

Если я переключаю ветвь pi_fix -> rev(pi_fix), то curl меняет знак строго по m_sign. Но нулевое равенство сохраняется. Поэтому уравнение инвариантно, а знак не спрятан в конвенции.

6. Вывод второго уравнения электростатики: div D = rho

Теперь я вывожу уравнение источника в статике.

6.1. Что такое D в моём языке

D — это L2-компонента дуального поля G. Я фиксирую в статике:

• G при L2-проекции распадается на ту часть, которая отвечает за «электрический поток»;

• эту часть я обозначаю D (индукция/электрическое смещение).

В вакууме или при простой конститутивной связи обычно пишут D = eps E, но это не относится к структуре электростатики как канона: это отдельный слой «материальных соотношений». Здесь я его пока не использую.

6.2. Источник в статике: только rho

Во второй корневой формуле:

dG = J

в статике:

• токовая часть J_vec = 0,

• остаётся только плотность заряда rho.

То есть L2-проекция источника даёт:

J -> rho

6.3. Дивергенция как распаковка dG = J

На L2-уровне уравнение dG = J превращается в утверждение о дивергенции D:

Поскольку div_{pi_fix} := *_{pi_fix} o d o *_{pi_fix}, а D — соответствующая “потоковая” компонента дуального поля, получаю:

div_{pi_fix}(D) = rho

В школьной записи:

div D = rho

6.4. Закон сохранения здесь встроен автоматически

Применяя d к dG = J, я получаю:

dJ = d(dG) = 0

В статике это согласуется с тем, что rho не обязана «исчезать» или «появляться» без токов: любой разрыв сразу был бы отловлен гейтом комплекса.

7. Что я получил в конце главы 2

Я вывел канон электростатики как L2-распаковку корневых формул при статических ограничениях:

1. из dF = 0:

curl E = 0

1. из dG = J при J_vec = 0:

div D = rho

И главное:

• curl и div у меня не первичные и не зависят от «правила правой руки» как скрытой договорённости;

• они определены как композиции через d и *_{pi_fix}, а знак управляется pi_fix/rev через m_sign.

8. Что остаётся

В Главе 3 я закрою «жёсткость» электростатики:

• задам класс допустимых альтернатив C_ES (локальность, первый порядок, линейность, ветвевой знак, запрет hidden join, типизация M/R);

• формально введу группу эквивалентных представлений G_repr(pi_fix) именно для электростатики;

• покажу, что любая альтернатива либо эквивалентна канону (curl E = 0, div D = rho) через G_repr, либо обязана указать, какой гейт она ломает.

Глава 3. Теорема жёсткости электростатики: почему «альтернативы» либо эквивалентны канону, либо ломают гейты

1. Цель главы и формат утверждения

В главах 1–2 я зафиксировал канон электростатики как L2-проекцию корневых формул при статике:

• из dF = 0 следует curl E = 0,

• из dG = J при J_vec = 0 следует div D = rho.

Теперь я закрываю то, что делает вывод не «пересказом диффформ», а жёсткой аксиоматикой: я определяю класс допустимых теорий электростатики C_ES и доказываю, что внутри этого класса любой честный вариант либо:

1. сводится к канону через допустимую смену представления (элемент G_repr(pi_fix)), либо

2. обязан нарушить хотя бы один гейт (локальность, ветвевой знак, D o D = 0, типизация M/R, запрет hidden join и т.п.).

2. Класс допустимых электростатических теорий C_ES

Под «альтернативой электростатики» я понимаю не произвольную фантазию, а строго ограниченную тройку объектов:

• D — кандидат на локальный дифференциал/границу первого порядка;

• S = *_{pi_fix} — кандидат на ветвезависимую дуальность;

• Eq_ES — электростатические уравнения (локальные, линейные, первого порядка) для полей и источников.

Я фиксирую класс C_ES набором условий (гейтов) — это те же принципы, что в общем выводе Максвелла, но заточенные под статику.

ES-C1. Локальность без скрытого join

Все операторы используют только локальную смежность (в дискретной модели — радиус 1 по комплексу/графу). Любое «склеивание дальнего» допустимо только как явно помеченный join_stage с join_id. В противном случае это hidden join и теория вылетает из класса.

ES-C2. Первый порядок

В уравнениях используются только операторы первого порядка: D и S o D (и, где нужно, S o D o S). В качестве базовых кирпичей запрещены вторые производные/вторые разности типа D(D(...)), кроме как в форме структурной проверки D o D = 0.

ES-C3. Линейность на каноне

Уравнения линейны по полям и источникам (E, D, rho) и по их первому производному (через D). Нелинейности — это уже другой класс теорий, и их нельзя выдавать за «альтернативу того же уровня».

ES-C4. Ветвевой знак

Существует ветвь pi_fix и инволюция rev(pi_fix), при которой знак дуальности меняется строго:

*_{rev(pi_fix)} = m_sign *_{pi_fix}, где m_sign ∈ {+1, -1}, и rev(pi_fix) => m_sign := -m_sign.

Следствие: все производные L2-типа (curl, div) меняют знак предсказуемо, а не «по вкусу автора».

ES-C5. Типизация M/R не смешивается

Операторы и поля типизированы: то, что живёт в секторе M, не смешивается с R без явного Dual/*. Любая подмена типов — нарушение.

ES-C6. Структурный закон комплекса

Как только я допускаю «границу/обход», я обязан иметь:

D o D = 0

Это не физика, а логическая непротиворечивость понятия границы.

ES-C7. Статический режим

Внутри C_ES я работаю при:

∂/∂t = 0, J_vec = 0.

Это фиксирует предмет электростатики: остаётся rho.

3. Группа допустимых преобразований представления G_repr(pi_fix) в электростатике

Чтобы слово «эквивалентна» было строгим, я задаю класс преобразований, которые считаю чисто координатными (не меняют L2-канон при фиксированном pi_fix).

Элемент T ∈ G_repr(pi_fix) — это семейство локальных изоморфизмов по рангам:

T_k: Ck -> Ck (обратимы и локальны)

таких что:

(G1) Коммутация с дифференциалом

T_{k+1} o D = D o T_k

Смысл: я меняю базис/представление на клетках, но не ломаю структуру комплекса.

(G2) Переориентации (знаковые инволюции)

Разрешены R_k со свойством R_k^2 = I и тем же условием согласования с D. Это формализует то, что обычно скрывают как «смена ориентации».

(G3) Сопряжение дуальности

Дуальность может меняться сопряжением:

S' = T_{n-k} o S o T_k^{-1}

но при условии сохранения ветвевого закона:

S'_{rev(pi_fix)} = m_sign * S'_{pi_fix}.

(G4) Сохранение типизации M/R

Преобразование блочно:

T = diag(T_M, T_R)

и не смешивает сектора.

(G5) Инвариант «no hidden join»

Если T_k использует дальние клетки или скрытую агрегацию, это вне G_repr.

Итого: G_repr(pi_fix) — это разрешённый класс «смены записи», который покрывает базисные/координатные/ориентационные свободы, но запрещает нелокальные магии.

4. Леммы, которые «убивают» альтернативы в классе C_ES

Лемма ES-1. Любой допустимый D в C_ES эквивалентен каноническому d

Если D локален и D o D = 0, то он реализует структуру цепного комплекса. В классе носителей, где определены стандартные инцидентные матрицы (граф/клеточный комплекс), любой такой D отличается от стандартного d лишь локальной перебазировкой/переориентацией, то есть элементом G_repr(pi_fix).

Замечание о строгости (честно, но без уступок): это место, где критик обычно требует явного ограничения класса носителей (регулярные CW-комплексы, стандартные решётки и т. п.). Я фиксирую: в C_ES носитель локальности принадлежит классу, где инцидентная структура определяет корректный клеточный комплекс, и где локальная перебазировка является допустимой.

Лемма ES-2. Ветвевой знак фиксирует S с точностью до G_repr(pi_fix)

Если S не удовлетворяет ветвевому закону, то при смене pi_fix знаки в curl/div перестают быть детерминированными, и теория теряет проверяемость. Следовательно, допустимые S отличаются лишь сопряжением в G_repr(pi_fix).

Лемма ES-3. В статике уравнение curl E = 0 неизбежно (иначе ломается D o D = 0 или локальность)

В классе первого порядка любой «вихрь» есть композиция S o D. Если я пытаюсь сделать в статике уравнение вида:

curl E = K

где K — ненулевой локальный линейный функционал (без источников времени), то я либо:

• вынужден ввести дополнительные структуры, которые фактически являются скрытым join (чтобы согласовать K на всех локах), либо

• нарушаю ветвевую дисциплину (потому что K должен тоже правильно менять знак при rev(pi_fix)), либо

• повышаю порядок (получается не электростатика первого порядка).

Поэтому в C_ES статическое поле без вихревых источников обязано быть замкнутым: dE = 0, значит curl E = 0.

Лемма ES-4. В статике div D = rho — единственный честный способ ввести заряд

Если я постулирую уравнение источника в форме

D(G) = rho

то применение D к обеим сторонам даёт:

D(D(G)) = D(rho) => 0 = D(rho)

То есть «заряд» обязан удовлетворять структурному условию совместимости с комплексом. Любая попытка встроить rho нелокально (например, rho(x) зависит от далёких значений поля) нарушает локальность и попадает под гейт hidden join.

5. Теорема жёсткости электростатики

Теперь формулирую результат в форме, которую можно вшивать в SPEC/ledger.

Теорема (жёсткость электростатики в классе C_ES). Пусть электростатическая теория задана тройкой (D, S, Eq_ES) и удовлетворяет условиям ES-C1..ES-C7. Тогда существует преобразование представления T ∈ G_repr(pi_fix) такое, что после переноса через T:

1. оператор D приводится к каноническому d,

2. дуальность S приводится к *_{pi_fix} (с сохранением ветвевого закона),

3. уравнения Eq_ES приводятся к канону:

curl E = 0 div D = rho

где curl := *_{pi_fix} o d, div := *_{pi_fix} o d o *_{pi_fix} на согласованном ранге.

Иными словами: внутри C_ES нет «другой электростатики». Есть только разные записи одной и той же структуры, либо нарушение гейтов.

6. Один явный «контрпример-альтернатива» и где он ломается

Чтобы тезис не выглядел декларацией, я показываю типовой приём, который часто пытаются выдать за «новую физику», хотя это либо нелокальность, либо скрытая склейка.

Контрпример A: нелокальная поправка к закону Гаусса

Пусть кто-то пишет:

div D = rho + α * Laplacian(rho)

(или в дискретном виде — добавляет вторую разность по решётке).

Что здесь происходит:

• Laplacian(rho) — оператор второго порядка: это нарушение ES-C2 (первый порядок).

• В дискретной реализации это почти неизбежно использует «соседей соседей», а часто и дальние зависимости: это риск нарушения ES-C1 (локальность) или превращение в скрытую агрегацию.

• Кроме того, если автор не прописал ветвевую дисциплину для каждого дополнительного члена, он ломает ES-C4.

Итог: такая «альтернатива» не является альтернативой электростатики в моём классе. Это другая теория (другой класс допущений), и она должна честно заявить, какой гейт снят.

Контрпример B: “скрытая склейка” в потенциале

Ещё типичный ход:

E = -grad(phi) + IntegralKernel * rho

где IntegralKernel — интегральный оператор по области.

Это немедленно нарушает ES-C1 (локальность): появляется дальнодействие как базовый кирпич. В моей дисциплине это допустимо только как явный join_stage с join_id, а не как скрытая «подстановка».

7. Что я считаю «достаточно строгим» в плане математики

Я фиксирую границу применимости, чтобы критик не атаковал “не теми” вопросами.

1. Я работаю в локальном режиме на носителях, где корректно определён комплекс и действует D o D = 0.

2. Глобальная топология (нетривиальные ко-гомологии, глобальные классы, заряд как класс и т. п.) — это отдельный слой. Он не отменяет канон, но меняет пространство решений (появляются глобально нетривиальные конфигурации).

3. Материальные соотношения (D = eps E и т. п.) — не часть «аксиоматики вихря/границы», а отдельный конститутивный слой.

8. Финальный вывод всей электростатической трилогии

В строгом классе допущений, который я обозначил как C_ES, электростатика не выбирается и не «подгоняется». Она возникает как:

• структурное следствие d o d = 0 (логики границы),

• ветвевой дисциплины дуальности *_{pi_fix} и знака m_sign,

• и честной L2-проекции без скрытых соглашений.

Поэтому:

• curl E = 0 и div D = rho — это не эмпирические формулы, а канон, вынужденный структурой.

• Любая «альтернатива» либо эквивалентна канону через G_repr(pi_fix), либо должна указать, какой гейт снят (локальность, первый порядок, ветвевой знак, типизация, запрет hidden join).

Вопросы по статье можете задавать в среде ChatGPT, просто вставьте архив и инструкции в первое сообщение чата.

Читайте также:

Опровержение» теории Большого взрыва? Как Вселенная могла возникнуть в форме вихря (многополярной спирали)

От локальности границы к полям: буравчик в многополярной спирали L1–L4 и максвелловские тождества

Выводим уравнений Максвелла из четырёхполярности L4 и вихря L2–L3–L4 (часть 1)

Иллюзия трёхмерного пространства: строгий анализ зрительного и тактильного восприятия

Как вывести уравнения Максвелла из четырёхполярности (L4) — без шуток и без подгонки под учебник

Правильные кватернионы (кватернионы В. Ленского) как строгая суперпозиция четырёхполярных лок (часть 1)

ИИ не источник истины, а исполнитель допуска. Гейты как дисциплина допуска: как архив, граф и ИИ удерживают многополярную логику

Гравитация и время!

Лока4 (L4): просто и понятно о четырёхполярности

Четырёхполярность (L4) простым языком. Истинная природа электромагнетизма

Граф и архив как матрица мышления: как я создаю разумный ИИ

Трёхполярное пространство в L3-логике: почему мы живем в двухполярной «плоскости»

Что такое гравитация и время?

Что такое гравитация? Исчерпывающая статья в формате двухполярной L2-логики

Как из двухполярности естественно получается «энтропийная стрела времени» и почему превращение шкалы в сущность рождает ложные парадоксы

P. S. Ребята, не стесняйтесь спрашивать! Если где‑то логика показалась вам не совсем прозрачной или захотелось больше деталей — пишите, буду рад разобраться вместе. Мой ответ будет подробным, понятным и по делу. Для меня очень ценно каждое мнение: именно ваши вопросы помогают делать блог лучше. Все ваши комментарии я обязательно возьму на заметку для будущих статей.

Небольшое пояснение для тех, кому это показалось «новой физикой»

Если при первом чтении показалось, что здесь «придумана другая электродинамика» — это не так и одновременно именно так, в хорошем смысле.

• В математической физике уже давно существует координатно‑свободная запись уравнений Максвелла в виде двух формул dF=0 и dG=J с оператором границы d и дуальностью (Hodge‑звездой).

• В численных методах есть дискретный exterior calculus, где div и curl не постулируются, а определяются как композиции того же d и дуальности на клеточном комплексе.

То, что делается в этой статье, — это не «магия вместо Максвелла», а максимально жёсткая версия той же программы:

• берётся стандартная структура d с законом «граница границы = 0»,

• вводится явная дуальность и статический режим,

• добавляется дисциплина ветви/знака и запрет скрытых склеек (hidden join),

• и дальше показывается, что классические формулы электростатики curlE=0 и divD=ρ неизбежно вываливаются как L2‑проекция, а не как набор традиционных «правил».

В этом смысле да, это «новая физика» — но не по предсказаниям, а по логике: не меняются уравнения Максвелла, меняется уровень прозрачности того, какие именно структурные допущения за ними стоят и какие «альтернативы» на самом деле лишь переобозначения.

Вы можете также обсудить этот пост на форуме dxdy:

https://dxdy.ru/topic162246.html

Проблема: Уже несколько месяцев мы топчемся на месте. Простейшие примеры он понимает (раскрыть скобки, односложные действия с дробями, простейшие уравнения). Даже сокращённое умножение освоили. Решает нормально, пока это упражнение на одну механику.

Но как только пример становится чуть более сложным, с применением нескольких механик (например, применить формулу сокращённого умножения + раскрыть скобки с отрицательным множителем) - он напрочь забывает даже простейшие правила типа перемены знака или распределительного закона. Испаряется понимание смысла переменных. Выдаёт такую кашу, как будто первоклассника за интегралы усадили.

Возвращаемся опять к простейшим примерам на одну тему - снова решает без проблем. У меня есть подозрение, что на самом деле он логики происходящего нихрена не понимает, а просто заучивает порядок действий на простых примерах.

Он психует. Я тоже. Ругается, рвёт тетради, ломает ручки. Я стараюсь держать себя в руках. Но это же пиздец, как можно писать 2а+3б=5аб на полном серьёзе, при том что мы месяц долбаем эту тему?!

Вопрос: Может, для обучения взрослых нужны какие-то особые методики, а обычная детская программа не годится? Надо больше упражнений? Какие-то особые упражнения, учебники? Количество перерастёт в качество, или это всё вообще бесполезно?

Ну учили же как-то в советское время взрослых людей школьной программе. Подскажите, что делать?!

Вот так выглядит наша тетрадь после сегодняшнего занятия... И так каждый раз, когда я пытаюсь дать что-то сложнее односложных упражнений на одну тему

1. Ты читаешь чужое мнение и чувствуешь раздражение.
   — Потому что человек не прав?
   — Или потому что он вообще посмел говорить не как ты?

2. Когда споришь — ты хочешь понять или убедить?

3. Когда тебе пишут “ладно, ты прав” —
   ты чувствуешь радость или опустошение?

Если выбрал второе хотя бы раз —
значит, в тебе говорит не мысль, а защита.

⚙️ Почему спор всегда превращается в драку

Наш мозг не различает “несогласен” и “напали”.
Любое “ты не прав” обрабатывается как микросигнал угрозы.
Тело готовится защищаться: пульс учащается, дыхание рвётся, внимание сужается.
Дальше уже не важно, о чём мы спорим —
важно, кто победит.

Мы не ищем смысл.
Мы ищем подтверждение собственной целостности.
Пока логика спорит, страх просто держит щит.

🧩 Когда “ум” становится оружием

Чем умнее человек, тем изощрённее его защита.
Глупец просто орёт.
Умный — аргументирует.
Оба делают одно и то же: прячут уязвимость.

Парадокс в том, что правда часто живёт по другую сторону правоты.
Чтобы дойти до неё, нужно рискнуть остаться безоружным.
Не защищать идею — смотреть на неё, как на живое существо, которое может умереть.

🔄 Эксперимент, который не любят ни эго, ни алгоритмы

Когда в следующий раз кто-то не согласится с тобой —
попробуй не отвечать.

Не потому что ты слаб,
а потому что любопытен.

Посмотри, как внутри поднимется волна:
“Ну скажи хоть что-нибудь!”
И просто останься в этом чувстве.

Если ты выдержишь паузу —
ты поймёшь, что спор живёт не между людьми, а внутри каждого.
И что тишина — это не поражение, а проверка на зрелость.

🎭 Как работает Клоун

Клоун не учит.
Он вытаскивает из человека реакцию, чтобы тот увидел себя в действии.
Провокация — не ради боли, а ради осознания:
“Смотри, ты снова защищаешься.”

Иногда это раздражает. Иногда ранит. Иногда смешит.
И вот там, где больно или смешно — происходит движение.

Клоун не враг. Он просто не даёт тебе спрятаться за ролью “правильного”.

🤹 Исповедь (только без пафоса)

Расскажи про спор, где ты понял, что был неправ. Необязательно мне, расскажи себе, мысленно.
Не чтобы каяться. А чтобы увидеть, как твой собственный алгоритм работал на автопилоте.

Это не терапия. Это тренировка осознанности.
Честность — это не стыдно. Стыдно — прожить жизнь, так ни разу и не заметив,
кто именно внутри тебя так яростно хочет быть прав.

🜍 Финал, который на самом деле начало

Мозг не хочет понимать.
Он хочет побеждать.

Понимание начинается в тот момент,
когда ты перестаёшь считать победу целью.

Иногда правда — не награда, а потеря.
Потеря иллюзии, что ты лучше, умнее, у тебя длиннее.

И именно в эту секунду, когда ты больше не доказываешь —
ты наконец становишься человеком,
а не системой защиты собственного мнения.

Клоун не ломает людей. Он ломает их автоматизмы.

И если тебе сейчас немного больно —
значит, всё работает.

💡 Зачем всё это

Я не хочу, чтобы ко мне приходили ради картинок, мемов или клубнички.
Я хочу, чтобы приходили ради мысленного удара.
Чтобы оставались только те, кто чувствует этот огонь под рёбрами - желание понять,
а не те, кто ищет развлечение.

Это не контент.
Это лаборатория, где я разбираю себя/человека по алгоритмам и собираю обратно — уже живым.

Комментарий для погружения: Осознайте, какая кнопка — ваша. Не пишите пока. Просто запомните это ощущение. Это — ваша стартовая точка.

ЧАСТЬ 2: ЛАБОРАТОРИЯ — РАЗБИРАЕМ АЛГОРИТМ НА ДЕТАЛИ

Вы не «лентяй» и не «тревожный человек». У вас просто очень старая и громкая программа. Давайте посмотрим на ее код.

• Если ваша кнопка «Безопасность»: Ваш главный алгоритм — «Предсказание катастрофы». Он эволюционно полезен, но сейчас он просто парализует вас, бесконечно моделируя провалы.

• Если ваша кнопка «Справедливость»: Ваш скрипт — «Внешний локатор контроля». Он ищет причину ваших неудач вовне, лишая вас силы что-то изменить внутри.

• Если ваша кнопка «Вина»: Ваше ядро — «Перфекционизм как щит». Он не дает вам начать, потому что идеальный результат недостижим, а значит, пытаться бессмысленно.

Комментарий для погружения: Узнали свой код? Напишите одно слово в комментах: «Безопасность», «Справедливость» или «Вина». Давайте соберем данные для статистики.

ЧАСТЬ 3: ПЕРЕПРОШИВКА — МЕНЯЕМ КОД БЕЗ ПАНИКИ

Осознание — это 80% работы. Остальные 20% — это запуск нового паттерна. Не бойтесь, мы не будем «ломать» вашу личность. Мы просто установим патч.

• Для кнопки «Безопасность»:

  • Старая программа: «Избегать ошибок».

  • Новый патч: «Любая ошибка — это данные для эксперимента. Я — ученый в лаборатории своей жизни».

  • Задание: Совершите одну микро-ошибку сегодня нарочно (опоздайте на 5 минут, отправьте сообщение с опечаткой). И проследите, не рухнула ли Вселенная.

• Для кнопки «Справедливость»:

  • Старая программа: «Ждать, когда мир станет честным».

  • Новый патч: «Моя сила — в моих реакциях и выборах. Я беру ответственность за свой кусок реальности».

  • Задание: Найдите одну ситуацию сегодня, где вы можете сделать первый шаг, не оглядываясь на других. Сделайте его.

• Для кнопки «Вина»:

  • Старая программа: «Я должен быть идеальным».

  • Новый патч: «Достаточно быть «достаточно хорошим». Завершенное неидеальное действие лучше, чем идеальное в воображении».

  • Задание: Сознательно сделайте какое-то дело на «троечку» и похвалите себя за его завершение.

Эпилог: Куда движемся дальше?

Если вы дочитали до этого места, значит, ваш внутренний Клоун уже проснулся. Он задает вопросы. Он сомневается в старых схемах.

Это не конец. Это начало диалога.

Что дальше? Ваш ход:

1. Для пассивных зрителей: Просто поставьте «+» в комментах, если хоть одна мысль здесь зацепила.

2. Для любопытных: Напишите слово своей кнопки и один вопрос, который у вас остался.

3. Для готовых к действию: Напишите «Эксперимент» — с символом @VadimRo, Тогда сообщение отобразится у меня на странице «Мои сообщения». Придумаем, как обсудить: лично или публично)

Пикабу, я — Клоун. И я только что показал вам фокус с вашим собственным сознанием. Вы все еще думаете, что это просто шутка?

1+1=2 - это арифметическое сложение в системах счисления, чье основание равно 3** и больше. Для арифметического сложения в разных системах счисления 1+1=10_2 и 1+1=2_10 эквиваленты. 10_2 - 10 с нижним индексом 2, 2_10 - 2 с нижним индексом 10. Нижний индекс определяет основание системы счисления. Для человека по умолчанию считается нижний индекс равный 10, для компьютера нижний индекс равен двум, поэтому в специализированной литературе нижние индексы могут не записываться.

*) отдельная логика сумматоров, если кратко: сложение двух бит _a_ и _b_ определяется набором: старший бит _с_=_a_*_b_ (двоичное И), младший бит (_a_ xor _b_). Это получен полусумматор. Только вот второй разряд _c_ (один или ноль в уме) нужно прибавить к соответствующим _a_ и _b_ следующего разряда, поэтому сложение реализовывается для трех разрядов - a,b и перенос с предыдущего разряда или два полусумматора дают один сумматор.

**)Не все виды троичной системы счисления подходят, т.к. там есть сбалансированный вариант троичной системы вида (-1, 0, 1), соответственно, двойки в ответе не будет (визуально не будет, по смыслу она там будет и будет записана иначе).

Люди могут плохо знать такие нюансы математики, что она не ограничивается арифметикой. Арифметика - это лишь один из разделов математики. Математика включает и другие разделы: булевая алгебра, теория графов, теория множеств, статистика, дифферинциальное исчисление и т.д. Либо быть просто дурачками по жизни.

Я склоняюсь к первому варианту, что люди просто не знают и их можно просвятить. Что мир сложнее, чем написано в школьном учебнике за первый класс. Но почему люди достаточно часто пытаются доказать, что я ошибаюсь и на самом деле они относятся ко второй группе? Как будто такие люди родились в семье двух таксистов, которые тайно правят миром не привлекая внимание психиатров.

- Фрукт - фрукт, сиська - сиська, цветок - цветок, тоже самое, мать твою.

- Да, капитан, они довольно похожи. (...) [Первая картина - работа известного художника]. А [вторая картина] просто мерзость.

Заметили? "Эксперт по одинаковости картин" находится в звании капитана! У него действительно может быть маленький [пиратский?] бизнес и он действительно управляет крупной организацией - командой корабля. И он действительно может повлиять на мир, убивая ученых и важных персон.

"Миром правит не тайная ложа, а явная лажа" (с) Пелевин