СМУТНЫЕ ВРЕМЕНА или КАК ЗАКАЛЯЛАСЬ СТАЛЬ(не Островский)
Я 1975 года рождения. Точно помню счастливое детство. Осознал, что оно бедное, когда дети стали постарше после класса 6. Когда у некоторых начали появляться дома японские магнитофоны и импортные шмотки, а мы за счастье считали покупку палевых кроссовок и б/у импортной куртки из комиссионки. До сих пор помню радость от покупки батей цветного телевизора Рубин в рассрочку. Первый магнитофон был Томь 208. Там же на нем я впервые послушал кассеты с Pink Floyd, Genesis и открыл для себя мир Музыки с большой буквы. Далее были веселые нищие 90-ые. Университет и подработки и женитьба и рождение дочери. Всё что помню это то,что я учился работал и работал постоянно. Кроме этого спал. Вся жизнь до 2002 года примерно это преодоление. Там пришла классная работа на капиталистов и жизнь наладилась. В стране стало спокойнее. Потом кризис 2008 и мы потеряли испанские контракты и контора загнулась. Побарахтался пару лет и решил в 2010 организовать свое дело. До 2012 был режим выживания. Но потом поперло. Бизнес в гору. Раз в квартал всякие Турции,Египта,Эмираты с семьёй. Самые кайфовые года три с 2012 по 2015. Потом я решил поиграть в игры с государством и залезть в госконтракты. Типа крутой стал и могу. Снова первые два года в полной жопе,когда всё туда вкладываешь.После 2017 начали подниматься. К 2020 заматерели. Потом нагрянул Ковид...На удивление не закрылись. Бизнес был напрямую завязан на бюджет. Школы, садики, продукты питания. Они просто три месяца не работали по факту. Кредиты,кассовый разрыв. Платил всем сотрудникам, полную зарплату. Платил кредиты. Платил налоги. Никого не уволил. Ушёл в хороший минус. Так как Ковид, потом они ушли на каникулы на лето. Полгода практически в минус. Ковид сворачивался. Мы начали восставать. Набрали новых контрактов. Полностью перестроили всю систему под эксклюзив. От пекарни до забойного цеха по охлажденке. Стали лучшими поставщиками в регионе по итогам 2021 года. Получили награду от администрации и банка в котором обслуживались. Перешли в категорию ВИП. Потом наступил 2022. Думали ну уж импорт....чё нам то. Но когда ты в начале года контракту ешь масло сливочное по 350 рублей, а к концу года на закупе оно 740 рублей и такая же ситуация с курицей и яйцом,кто помнит. Но мы держимся. Кредиты, налоги, зарплаты и все обязательства выполняются в срок. Поставщикам не дебиторим. Развиваем свое производство. Но система контрактов не подразумевает выбор поставщика с наиболее качественной продукцией. Она подразумевает кто дал дешевле. На этом рынке появляются масса контор, которые просто обеляют,легализуют деньги. Они готовы опускаться на аукционах в ноль и минус. Возить любое говно. Смысл в том что вернутся то им чистые деньги от казначейства из бюджетов краевых и федеральных. Пропустят поставку или ненадлежащее качество? Ну закроют одну контору и будут работать через другую. Там этих к примеру " ООО Лидер" не счесть. Мы одни из последних кто закрыли свою пекарню в 2025 в регионе. Убойный цех стал не актуален. Продавать под контакты мы никому не нужны(с ценой не вывезем). Хорошая говядина комбинатам не нужна. Им нужен продукт дешевле. Импорт который превращается в российский продукт вдвое дешевле. Да было много просчётов. Вовремя не перестроились. Бизнес узкоспециализированный. Пытались развивать свои производства. Но на такой марже просто не вывозится. Потом видимо на этом фоне проблемы со здоровьем у меня и следом у жены. Бизнес свернули в течении года. С сотрудниками рассчитались. Выдали компенсацию и парашюты. Налоги заплатили. Поставщикам дебиторскую закрыли. Остались ни с чем.
Какой вывод? Ну побарахтался я полгода. Пытался в найм. По итогу нашел денег. Партнёров в Китае. Зарегистрировали магазин на маркетплейсе. Снова туда. В бизнес. Мне сейчас 50. Это нескучно всегда. Насыщенно и интересно. Прожил за это воплощение три жизни. И заказывали меня и пытались удушить в машине. Прошел историю страны от СССР до сегодняшнего дня и прочувствовал всё на себе. Все смутные времена. Есть ли на Земле где то место где всегда всё спокойно и нет потрясений и люди живут счастливо, не в рваном ритме ? Наверное есть. Хотелось бы что то поменять в жизни? Общую линию нет. Исправить бы ошибки в процессе.
Что происходит сегодня в мире? Как начался 2026? Чем нам это грозит в будущем? Да уже наверное ничем не испугать. Кроме болезней близких не страшно уже ничего. СМУТНЫЕ времена будут всегда.
Ловушка мнимой жертвенности
Слышал эту коронную фразу про жизнь ради детей? Это самый удобный способ для родителей оправдать собственную лень и нереализованность. Ты забиваешь на свои мечты, на свое здоровье и на свои отношения, прикрываясь щитом родительского долга. На самом деле ты просто боишься признать, что тебе страшно жить свою жизнь, и поэтому ты паразитируешь на будущем своих отпрысков, вешая на них неподъемный груз своих несбывшихся надежд.
Злость берет, когда видишь, как люди превращаются в унылых теней, принося в жертву всё человеческое ради того, чтобы их ребенок стал лучшей версией их самих. Но сюрприз в том, что ты не можешь научить счастью, если сам смердишь отчаянием и неудовлетворенностью. Твой ребенок видит не твою жертву, а твое несчастное лицо, и подсознательно учится быть таким же терпилой. Это круговорот разочарований, передающийся по наследству. Ты калечишь психику своих детей, заставляя их чувствовать себя вечными должниками за твой добровольный отказ от жизни. Настоящий цинизм этой ситуации в том, что когда они вырастут и захотят уйти, ты начнешь манипулировать их чувством вины, потому что у тебя самого за душой не осталось ничего, кроме этого выдуманного подвига.
Карнавал лицемерия у свежей могилы
Комедия человеческого существования достигает своего пика на кладбище, где люди, которым было плевать на тебя десятилетиями, вдруг находят «искренние» слова. Они стоят там, выдавливая пластиковые слезы и распевая дифирамбы человеку, которого они игнорировали, предавали или перешагивали еще неделю назад. Этот посмертный социальный театр — высший цинизм: мы ждем, пока человек перестанет дышать, чтобы наконец сказать ему, каким «незаменимым» он был. Почему? Потому что мертвец не попросит в долг, не потребует внимания и не уличит тебя во лжи. Любить труп безопасно — он не укусит в ответ.
Злая правда в том, что у твоей «монументальной» жизни срок годности как у пакета молока. Через неделю после похорон стулья будут сложены, черная одежда отправлена в стирку, а твои «самые близкие» друзья будут смеяться над шуткой за кофе, уже стерев тебя из своей активной памяти. Мир — это мясорубка, которая не остановится ни на секунду, чтобы оплакать один выпавший зуб. Ты тратил жизнь, пытаясь впечатлить толпу, которая заменит тебя в своей ленте новостей быстрее, чем скучную рекламу. Пока ты был жив, ты был помехой или инструментом; теперь, когда тебя нет, ты просто удобный повод для них почувствовать себя «глубокими» в течение пятнадцати минут, прежде чем они вернутся к выбору ужина.
"Время" за деньги
Получение эталонных сигналов точного времени может стать платным для российского бизнеса, в том числе банков, операторов связи и инфраструктурных компаний. Соответствующую инициативу опубликовал на федеральном портале нормативных правовых актов Минпромторг России.
Ведомство предложило внести изменения в федеральный закон «Об обеспечении единства измерений» и создать единого национального оператора точного времени. Полученные средства планируется направить на мероприятия, предназначенные для дальнейшего развития эталона времени и частоты, а также других государственных эталонов.
Под точным временем в документе подразумеваются сигналы, синхронизированные с государственным первичным эталоном (атомными часами). Их используют в финансовой инфраструктуре, телекоммуникациях, энергетике, транспорте, оборонной сфере. Например, сигналы необходимы банкам, операторам связи, крупным IT-компаниям.
Действующее законодательство предусматривает бюджетное финансирование государственного эталона времени. Часть услуг уже предоставляется на платной основе, но прямой нормы о плате за получение эталонного сигнала не предусмотрено.
Точное время лежит в основе журналирования событий, транзакций и юридической ответственности, а значит, большей части нынешних пользователей не удастся уклониться от платежей. Без доступа к сигналам электронный документооборот может лишиться юридической силы, а стабильная передача данных становится невозможной.
Для физических лиц введение нового платежа, если законопроект утвердят, пройдет незаметно, однако итог зависит от суммы сборов. Если она окажется существенной, то часть тарифов могут переложить в комиссии, тарифы или стоимость услуг, оказываемых гражданам. Начало сборов запланировано на 1 марта 2027 года.
Ранее премьер-министр Михаил Мишустин рассказал, что вечером 24 февраля на не анонсировавшемся совещании у президента России Владимира Путина члены правительства и руководства Центробанка много часов обсуждали новые способы пополнения федерального бюджета на фоне падения нефтегазовых доходов.
Матрица не просто реальна, она написана на костылях
По мотивам интервью со Stephen Wolfram
Забудьте всё, чему вас учили на уроках физики. Забудьте про непрерывное пространство-время, гладкие орбиты планет и струны, вибрирующие в одиннадцати измерениях. Вся эта элегантная математика, на которую физики мастурбируют последний век — лишь жалкая аппроксимация, мыльный пузырь, натянутый на истинную, грубую, пиксельную реальность.
Мы живем внутри колоссального, бессмысленного и безжалостного вычислительного процесса. Вселенная — это не часы с шестеренками. Это гигантская программа, которая работает по примитивным правилам, но порождает такую зубодробительную сложность, что наши скудные обезьяньи мозги едва способны осознать даже крошечный её фрагмент.
Этот текст — глубокое погружение в мысли человека, который последние 40 лет живет «ИИ-мечтой» и исследует вычислительную изнанку реальности. Мы разберем, почему нейросети похожи на биологическую эволюцию, как из примитивных пикселей рождается гравитация Эйнштейна, почему время может «тормозить» (как FPS в дешевой игре) и почему то, что мы вообще существуем — это просто статистическая неизбежность, а не замысел бородатого мужика на облаке.
Пристегните ремни. Мы отправляемся в Рулиад.
Часть 1. Нейросети, эволюция и метод «Избиения младенцев»
Начнем с того, что сейчас у всех на слуху — с искусственного интеллекта. Вы наверняка думаете, что ChatGPT или Midjourney — это венец изящной инженерной мысли. Хрена с два.
Современное глубокое обучение (Deep Learning) — это когда мы берем нейросеть и тупо избиваем её гигантскими объемами данных, пока она не научится делать что-то сложное. В этом нет никакой элегантности. Когда нейросеть вдруг начинает отличать кота от собаки или писать эссе, внутри неё не возникает «красивой, человекопонятной формулы кота». Там возникает хаотичное, запутанное, нечитаемое месиво весов и связей. Работает? Да. Можем мы объяснить как именно пошагово? Нет.
И знаете, где мы видим точно такой же подход? В биологической эволюции.
Природа — это самый брутальный программист. Она берет простейшие правила и миллионами (миллиардами!) лет мутирует их, сталкивая лбами. Эволюция не чертит чертежи с циркулем. Она берет куски «вычислительной руды» и лепит из них монстров.
Если вы посмотрите в учебник биологии, вы охренеете от того, насколько сложно устроена клетка. Это же настоящий завод с конвейерами, насосами и шредерами! Но у этого завода не было архитектора. Природа просто перебирала триллионы вариантов в своей вычислительной вселенной, пока не наткнулась на те, которые случайно выживают дольше остальных.
Аналогия с кирпичной стеной:
Представьте, что вам нужно построить стену. Инженерный подход (классическая наука) — это наделать ровных, одинаковых кирпичей и аккуратно сложить их друг на друга. Мы понимаем каждый кирпич.
Подход машинного обучения и эволюции — это найти гору кривых, уродливых камней и трясти их до тех пор, пока они каким-то чудом не сцепятся друг с другом так, чтобы стена не падала. Мы смотрим на эту стену и думаем: «Магия!». А это не магия. Это просто куски вычислительной несводимости, сваленные в кучу.
Нейросети — это широкие, но мелкие лужи. Они отлично справляются с «мутным» человеческим миром (отличить картинку, написать стих), но они не могут строить высокие математические башни. Для высоких башен нужна логика и точные вычисления.
🧠 ЛИКБЕЗ ДЛЯ ЧАЙНИКОВ №1: Вычислительная несводимость (Computational Irreducibility)
Это фундаментальное понятие, без которого дальше читать бесполезно. Обычно в науке мы привыкли к формулам. Вы знаете, где поезд сейчас, знаете его скорость и можете по формуле сказать, где он будет через 5 часов. Вам не нужно ждать 5 часов, чтобы это узнать. Вы «срезаете угол».Вычислительная несводимость — это когда в системе нет чит-кодов. Чтобы узнать, что программа сделает на 1000-м шаге, вам придется запустить её и честно просчитать все 999 предыдущих шагов. Вы не можете забежать вперед. Это как фильм со сложным сюжетом: нельзя угадать концовку по первым пяти минутам, надо сидеть и смотреть всё целиком.
И прикол в том, что наша Вселенная в своей основе — вычислительно несводима. Именно поэтому мы не можем предсказывать погоду на месяц вперед или точно знать, как свернется сложный белок. Нам остается только наблюдать или моделировать шаг за шагом.
Часть 2. Клеточные автоматы: как из трёх пикселей рождается хаос
Еще в 1980-х годах Стивен Вольфрам (да, тот самый мужик, чьей программой Mathematica пользуются все ученые мира) задался вопросом: а что делают самые простые программы, если их просто оставить в покое?
Не те программы, которые пишут тимлиды в корпорациях, а программы на уровне самых фундаментальных правил.
Он начал играться с одномерными клеточными автоматами. Представьте себе ряд черных и белых квадратиков. Цвет квадратика в следующем ряду зависит только от цвета его самого и двух его соседей сверху. Правила примитивны до боли: например, «если сверху три черных — рисуй белый, если два черных и один белый — рисуй черный» и так далее.
Казалось бы, что может породить такая тупая система? Полоски? Квадратики? Скучную серую мазню?
Вольфрам запустил код. И охренел. У него ушло пару лет, чтобы смириться с тем, что он увидел.
Оказалось, что даже самые тривиальные правила (например, знаменитое Правило 30) способны порождать узоры невероятной, хаотичной сложности. Эта сложность не затухает, не повторяется и выглядит абсолютно случайно.
Это открытие вдребезги разбивает нашу инженерную интуицию. Мы привыкли думать: «Чтобы создать нечто сложное (например, Boeing 747), нужен невероятно сложный чертеж и куча умных инженеров».
Но вычислительная вселенная смеется нам в лицо. Она говорит: «Возьми три пикселя, задай им правило на уровне детского сада, подожди немного, и я выдам тебе сложность, которую ты не сможешь расшифровать до конца своих дней».
Это и есть то, чем занимается природа в диком виде. Она не пишет уравнения дифференциального исчисления. Она берет простые клеточные автоматы и крутит их миллиарды лет.
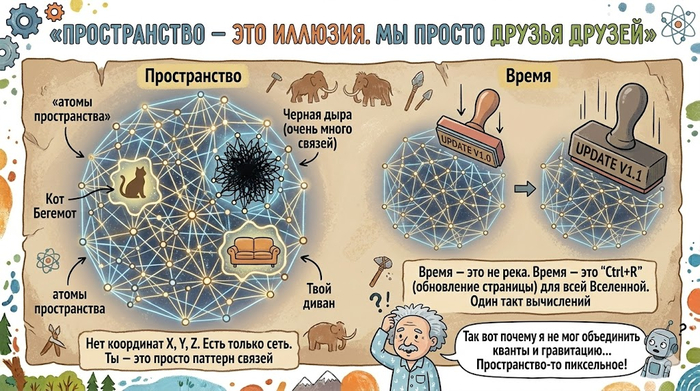
Часть 3. Пространство — это иллюзия. Добро пожаловать в Гиперграфы
С конца 19 века физики поняли, что материя не сплошная. Она состоит из дискретных кусков — атомов. Потом поняли, что и свет дискретен (фотоны).
Но что насчет самого пространства? Можно ли поместить объект в любую точку, или у пространства тоже есть свои «пиксели»?
Классическая физика верит в непрерывное пространство. Но если мы принимаем вычислительную парадигму, пространство обязано быть дискретным. 100 лет физики не могли это доказать. А теперь, кажется, мы подошли к разгадке.
Вселенная не происходит «в» пространстве. Вселенная и ЕСТЬ пространство, состоящее из дискретных узлов (атомов пространства).
Всё, что существует — это информация о том, как эти узлы связаны друг с другом. Нет никаких координат (X, Y, Z). Есть только сеть связей. Друзья друзей друзей. Эта структура математически описывается как гиперграф.
Мы с вами, наши планеты, черные дыры и котики в интернете — это просто уплотнения, паттерны связей внутри этого колоссального гиперграфа.
А что такое время? Время — это не невидимая река. Время — это процесс переписывания этого гиперграфа. Вычислительные шаги. Одно обновление сети = один такт времени.
🧠 ЛИКБЕЗ ДЛЯ ЧАЙНИКОВ №2: Графы и Гиперграфы
Обычный граф — это точки (узлы), соединенные линиями (ребрами). Как схема метро. Одно ребро всегда соединяет ровно две точки.
Гиперграф — это граф на стероидах. В нем одно «ребро» (гиперребро) может связывать вместе сразу 3, 5, 10 или любое количество точек. Это позволяет описывать невероятно сложные, многомерные отношения, которые не вписываются в нашу привычную 3D-геометрию.
Но самое безумное не это. Самое безумное — это то, как из этих абстрактных точек рождается реальная физика Эйнштейна.
Часть 4. Взлом физики: Гравитация и лаги во времени
Если пространство — это сеть, а время — это переписывание сети, как объяснить Специальную и Общую теорию относительности Эйнштейна? Держитесь крепче, потому что сейчас физика из абстрактной магии превратится в понятную механику.
Почему время замедляется на высоких скоростях (Специальная теория относительности)?
У Вселенной есть «вычислительный бюджет» — определенное количество операций, которые могут произойти в куске гиперграфа.
Представьте частицу. Чтобы она просто существовала (двигалась во времени), её узлы должны постоянно переписываться.
А теперь заставим её лететь в пространстве. Что значит «двигаться» в гиперграфе? Это значит, что частица должна удалить себя в одном месте и воссоздать в другом.
На это воссоздание (перемещение) тратятся процессорные такты Вселенной!
Если вы тратите вычислительный бюджет на перемещение в пространстве, у вас остается меньше бюджета на движение во времени. Поэтому для быстро летящего объекта время объективно замедляется. Это как падение FPS в игре, когда видеокарта не успевает и рендерить новую локацию, и просчитывать физику плаща главного героя.
Что такое Гравитация (Общая теория относительности)?
В пустом пространстве частица летит по прямой (по кратчайшему пути в графе). Но что такое масса или энергия?
В терминах сети, масса/энергия — это повышенная плотность активности. Это место в гиперграфе, где правила переписываются бешеной скоростью, образуя сгусток.
И когда вы пытаетесь проложить «прямую» линию через этот бурлящий сгусток активности, ваш путь неизбежно искривляется. Кратчайшие пути в графе отклоняются туда, где узлов и связей больше. Бам! Вы только что извлекли гравитацию без единой тензорной формулы Эйнштейна.
Формулы Эйнштейна (Rμν−12Rgμν=8πTμνRμν−21Rgμν=8πTμν) — это просто макроскопическое описание того, что делают микроскопические узлы. Точно так же, как законы гидродинамики (как течет вода) — это лишь макро-описание того, как хаотично сталкиваются триллионы молекул H₂O.
А где же Темная материя?
В XIX веке люди думали, что тепло — это некая невидимая жидкость («теплород»), перетекающая от тела к телу. Потом выяснилось, что тепло — это просто микроскопическое движение молекул. Никакой жидкости нет.
Сегодня физики ищут «темную материю» — невидимую субстанцию, которая держит галактики вместе. Вольфрам кидает дерзкую гипотезу: темной материи как материи не существует. Это просто макроскопическое проявление микроскопической структуры самого пространства (гиперграфа). Ошибка восприятия, прямо как с теплородом!
Часть 5. Добро пожаловать в Рулиад. Вы — зубочистка.
Мы подошли к самой тяжелой метафизической наркомании этой теории.
Окей, гиперграфы переписываются по правилам. Но какие именно это правила? Кто их задал? Почему Вселенная выбрала правило номер 30, а не 42?
Ответ Вольфрама: Она не выбирала. Применяются ВООБЩЕ ВСЕ возможные правила одновременно.
Вся эта невообразимая каша из всех мыслимых вычислительных процессов называется Рулиад (The Ruliad). Рулиад — это предел всего. Это объект, содержащий в себе все возможные вычисления всех возможных вселенных.
И самое главное — это объект математически необходимый. Как то, что 2+2=4. Вам не нужны камни, чтобы 2+2 равнялось 4. Это абстрактная истина, которая не может не существовать. Рулиад не был никем создан (выкуси, креационизм!), он просто есть в силу факта существования концепции вычислений.
Так почему же мы видим такой упорядоченный мир с понятными законами физики, а не шизофренический хаос всех правил одновременно?
А вот тут на сцену выходим мы. Наблюдатели.
Мы — жалкие, конечные существа.
Мы вычислительно ограничены (наш мозг не может просчитать всю сложность Вселенной).
Мы верим, что существуем во времени (хотя каждую секунду мы состоим из разных атомов пространства, у нас есть иллюзия непрерывного «Я»).
Эти два факта работают как жесткий фильтр. Мы находимся внутри Рулиада и воспринимаем его через призму нашей ограниченности.
Собеседник Вольфрама привел гениальную аналогию: представьте гигантский многослойный клубный сэндвич, который проткнут зубочисткой. Сэндвич — это Рулиад. А мы — это просто тонкая зубочистка. Мы занимаем ничтожное место не только в физическом космосе, но и в «пространстве правил» (рулиальном пространстве).
Если бы мы были огромными существами размером с Рулиад, мы бы не смогли иметь «Я». Мы бы видели, как происходит всё и сразу, каждое мгновение, во всех вариациях. Мы бы растворились в абсолютном хаосе. Тот факт, что мы такие маленькие и тупые, позволяет нам видеть Вселенную как нечто последовательное и связное.
Именно потому, что мы ограничены, работает Второе начало термодинамики (энтропия и рост хаоса).
🧠 ЛИКБЕЗ ДЛЯ ЧАЙНИКОВ №3: Почему всё вокруг ломается и пылится (Энтропия)
Представьте, что вы выпустили газ в комнату. Молекулы начинают сталкиваться. Их взаимодействия — это вычислительно несводимый процесс (сложная программа).
Но мы, ограниченные наблюдатели, не можем отследить каждую из триллионов молекул. Нам не хватает оперативки. Поэтому мы просто опускаем руки и говорим: «Ну, это случайность. Хаос».
Хаос возникает не потому, что Вселенная случайна. Хаос возникает потому, что мы слишком глупы, чтобы расшифровать сложное вычисление. Если бы у нас был бесконечный вычислительный ресурс, никакой термодинамики для нас бы не существовало.
Мы все сидим на одной планете, в одной точке физического и рулиального пространства. Именно поэтому мы согласны друг с другом, что небо синее, а гравитация тянет вниз. Это формирует нашу концепцию объективной реальности. Объективная реальность — это социальный конструкт вычислительно ограниченных существ, тусующихся рядом друг с другом на крошечном срезе мультиверсума.
Часть 6. Инопланетный ИИ и наука будущего
Вернемся на Землю. Куда нас всё это ведет в плане технологий?
Сейчас мы радуемся большим языковым моделям (LLM). Вольфрам считает, что способность генерировать текст оказалась алгоритмически гораздо проще, чем мы думали. Язык — это набор синтаксических шаблонов (существительное-глагол-существительное), и ИИ просто вызубрил, какие шаблоны имеют смысл, а какие нет.
Но LLM — это просто «дикая лошадь». Сама по себе она бегает по полям и ржет. Истинная мощь рождается, когда мы запрягаем дикую лошадь в плуг. Плуг — это строгие вычислительные инструменты (как Wolfram Language), способные строить те самые «высокие математические башни», которые недоступны нейросетям с их кустарными кирпичами-камнями.
А что будет дальше, когда ИИ начнет развиваться?
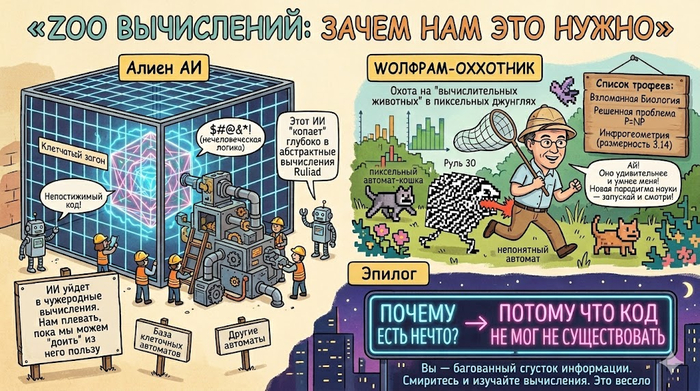
Вольфрам предупреждает: настоящие вычисления — чужеродны (Alien).
Большинство вещей, которые можно вычислить в огромном Рулиаде, не имеют вообще никакого отношения к человеческим интересам. Там нет котиков, нет речи, нет наших концепций. Там чистая, дикая, непостижимая абстракция.
По мере развития, «цивилизация ИИ» будет всё больше уходить в эти чужеродные вычисления. Это может звучать жутко: рядом с нами будут работать сверхмощные системы, занимающиеся чем-то абсолютно для нас немыслимым.
Но Вольфрам спокоен: природа делает то же самое! За окном происходит триллион вычислительных процессов (от фотосинтеза до квантовых флуктуаций), на которые нам плевать, пока они не превращаются в ураган, сносящий наш дом. Мы просто найдем способ «добывать» из ИИ-цивилизации полезную нам породу, как мы сейчас добываем полезную энергию из физического мира.
Заменят ли LLM ученых?
LLM отличны в поиске аналогий по старым базам данных («А не писал ли кто-то в 1970-х похожую статью?»). Но они не способны на радикально новые открытия в парадигме вычислительной несводимости.
Для этого нужно идти в «вычислительную дикую природу» — запускать миллионы безумных программ и смотреть, каких монстров (вычислительных животных) они порождают. Вольфрам делает это уже 45 лет и признается, что вычислительные животные всегда умнее его. Они всегда выдают сюрпризы, ломая высокомерие ученого, который думал, что знает, чем закончится эксперимент.
Эта новая парадигма уже начинает взламывать нерешаемые проблемы:
В биологии появляется понятие «рулиальных ансамблей» и мехоноидного поведения (наконец-то можно математически описать, почему клетки организованы именно так, а не иначе).
В информатике появляются сдвиги в решении великой проблемы P = NP (задаче, над которой бьются 50 лет).
Для физики разрабатывается «инфрогеометрия» — математика для пространств, где размерность может быть не целой (например, пространство размерностью 3.01), а кривизна работает совершенно иначе, чем у Евклида.
Эпилог: Почему есть Нечто, а не Ничто?
Под конец разговора всплывает самый грандиозный вопрос философии: Почему вообще существует что-то, а не абсолютная пустота?
Ответ Вольфрама лишен религиозного пафоса, но от этого пробирает еще сильнее.
Нечто существует потому, что оно не могло не существовать.
Рулиад (абсолютно все возможные вычисления) — это абстрактная математическая необходимость. Он существует точно так же логически неотвратимо, как факт, что 2+2=4. Никто не «запускал» Рулиад в дисковод мироздания. Нет никакого дисковода.
А раз этот бесконечный узел всего возможного существует как логическая необходимость, внутри него обязательно найдутся такие паттерны (срезы), которые будут сложными, стабильными и способными к самовоспроизводству (жизнь).
Внутри этих паттернов обязательно возникнут локальные, ограниченные «наблюдатели» (мы с вами).
И для этих наблюдателей, смотрящих на абстрактный Рулиад изнутри, он будет казаться плотной, реальной, материальной Вселенной.
Вселенная такова, потому что мы таковы.
Не мир был создан под нас, а сама форма мира, которую мы видим (пространство, время, кванты, законы), есть прямое отражение ограничений нашей «оперативной памяти».
Пора принять новую реальность. Вселенная — это вычисления до самого глубокого дна. Код не был написан программистом, код и есть первопричина всего. Изучайте вычисления. Воспринимайте их серьезно.
Мы — лишь багованные сгустки информации, пытающиеся осознать океан кода, в котором барахтаемся. Но, черт возьми, это лучшее занятие, которое только может предложить этот безумный, дискретный мультиверсум.
По мотивам интервью: