Ответ на пост «Про аксиомы»1
Я зачем-то прочитал весь пост. Хотел добраться до ошибки, будто у Лобачевского параллельные прямые пересекаются, но автор эту ошибку не допустил.
Почему я сразу со скепсисом отнесся к статье? По второму абзацу:
Когда у нас в пятом классе началась геометрия, нам так объяснили, что такое аксиома: это утверждение, настолько очевидное, что не нуждается в доказательствах. Наверное, пятиклассникам лучше этого не объяснишь, но проблема в том, что и в старших классах больше ничего об аксиомах не рассказывают.
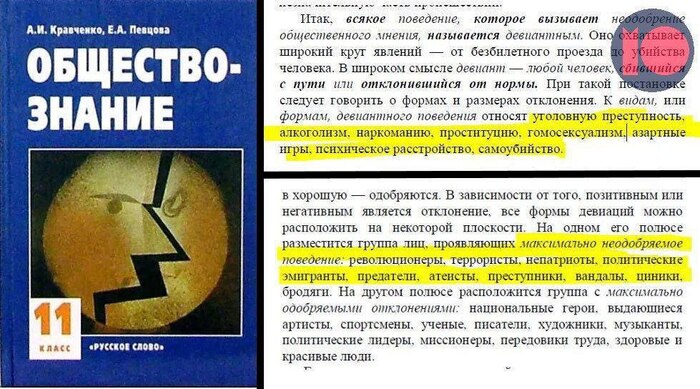
Если автор не учился в экспериментальной школе и если ему не девяносто лет, его геометрия не началась в пятом классе. Да, с 1933 года был учебник для пятиклассников - "Начальные сведения по геометрии" Гурвица-Гангнуса, хотя сомневаюсь, что там упоминались аксиомы. И сомневаюсь, что выпускники физмата МГУ написали в учебниках какую-то ересь. Хотя @Plexator 'у (это автор исходного поста) могло и не понравиться: в их учебнике за 6 класс аксиомы объясняются в физическом, а не математическом духе - но и не так, как сочинил @Plexator.
В любом случае с 1950-х годов в СССР были другие программы. Геометрию изучали по учебникам Киселёва или Никитина, и начиналась она только в 6 классе. Забавно, что у Никитина уже в самом начале курса написано ровно то, что хочет @Plexator:
И что тут неправильного?
Позже экспериментировали с другими программами по геометрии: Колмогорова, Атанасяна-Бутузова, Погорелова. Но никогда с 1950-х геометрию не начинали в 5 классе: геометрия начиналась в 6, а после перехода на 11-летнее обучение - в 7 классе.
И там про аксиомы написано всё правильно.
Конечно, элементы геометрии в курсе математики вводились и в ранних классах. Буквально в первом. Там про аксиомы ничего не говорилось.
Выходит, @Plexator плохо запомнил, чему и вообще когда его учили. После такого введения можно было ожидать любой ахинеи, но ничего суперошибочного автор не написал. В целом он говорит разумно, здраво, я с ним согласен.
Но по мелочевке проблемы вылазят. Например:
найдено сразу два пространства, которые описываются геометрией Лобачевского. Более того, эти пространства являются подмножествами евклидова пространства. Это значит, что любое утверждение из геометрии Лобачевского мы можем "перевести" на язык геометрии Евклида, причём истинное утверждение при таком переводе останется истинным, а ложное - ложным.
Два пространства? Что имеет в виду автор? Почему два, а не, например, штук около пяти, как в Википедии? С чего автор решил, что то, что "любое утверждение из геометрии Лобачевского можно перевести на язык геометрии Евклида", следует упростить до слов "пространство Лобачевского является подмножеством евклидова", что вообще автор понимает под словом "подмножество"?
Сдаётся мне, автор напутал. Он, наверное, имел в виду, что существует две геометрические системы, являющиеся неевклидовыми в узком смысле слова. Только вот одна из них - не Лобачевского.
Также непонятно, почему автор вообще утверждает, что "любое утверждение из геометрии Лобачевского мы можем "перевести" на язык геометрии Евклида, причём истинное утверждение при таком переводе останется истинным, а ложное - ложным". Есть масса утверждений, эквивалентных пятому постулату, и они, разумеется, в геометрии Лобачевского ложные, например о том, что накрест лежащие углы при параллельных и секущей равны, или что отношение длины окружности к диаметру есть константа, или что сумма углов треугольника равна развёрнутому углу, или что вокруг каждого треугольника можно описать окружность. Ничего этого в геометрии Лобачевского нет, как нет в ней прямоугольников и подобных треугольников.
Воспитание! Бить или не бить детей?
На работе есть приятельница, которая проработала учителем русского и литературы в школе прилично, а муж какой-то там потомственный математик, и естественно, на детях природа отдыхает.
Пацан в 6 классе, его перевели в новую школу двойки сыпятся как из рога изобилия. Решила мама с ним восполнить пробелы в учении по русскому языку, после двух часов проведенных с сыном над учебниками, силы ее иссякли и она взяв книжку в руки начала лупасить своего балбеса по голове приговаривая:
— Это просто ад какой-то, просто ад!!!
И забившись в истерике удалилась. Папаша тоже в унынии. На следующий день приходят родители с работы, и их встречает вымытая посуда, пропылесосеная квартира, короче кругом идеальный порядок, и крупными буквами на холодильнике на листе белой бумаги:
ДАБРО ПАЖАЛОВАТЬ В РАЙ!!!:)))))
Я учу биологию или почти нативная реклама
Хочу поступать в вуз на психолога (пока так).Для поступления надо готовиться к экзамену по биологии.Готовиться так готовиться.В школе я не особо любила биологию,не то что не любила,но без особо интереса ее учила.Больше любила порисовать во время урока или стихи пописать.Учительница была лояльная и спокойная,но излагала наверное тоже без особого вдохновения,90-е,какое там вдохновение..И вот после школы я хотела пойти учиться на психолога,но именно незнание биологии меня оттолкнуло от этого направления.Очень печально,ведь прошло 10 лет и я все-таки решили учиться именно на психолога😁.Может об этом подробнее потом напишу.Возвратимся к предмету "биология".Я взяла без особого раздумия учебник "Биология.Полный школьный курс",издательство Аверсэв,авторы:Лисов Николай Дмитриевич,Лемеза Николай Алексеевич,Камлюк Лилия Васильевна,Е.С.Шалапенок,М.В.Мащенко,Н.В.Акулич.
Учебник очень увлекательно написан,как будто тебе открывают двери в какие-то фантастичные миры и каждую составляющего этого мира просто и подробно описывают,прибегая к сравнениям и метафора,что делает процесс обучения не рутинным,а занимательным.Побольше бы таких авторов и таких учебников)
Еще мне нравятся термины биологические очень."Антоциан".Красиво,как имя прям.И словосочетания классные,для какой-нибудь инди-группы - "Тонкие нити цитоплазмы"🤔😁.Такие вот мысли про биологию.
А вам нравилась биология в школе?Для вас важная подача материала,или дело больше в интересе к предмету?
#биология #жизнь #учеба #школа #учебники #дляпоступающих
Как это работает?
Кто-нибудь из сведущих может мне объяснить феномен сего видео? Как человеку очень далекому от понимания процессов электричества в целом.