Сферическая эвольвента в трудах советских «файдоров»
«Видишь суслика? А он - есть!»
Удивительное дело: какой только ереси не написали славные ленинградские «файдоры»: Н.И.Колчин да, собственно, сам Файдор Л.Литвин - в своих «нетленных глыбах», но вот про сферическую эвольвенту - ничего внятного.
Вот пример настоящей ахинеи из Н.И.Колчина:
Угол зацепления - ноль! Шедеврально. Да и начальная плоскость инструмента скатывается, между прочим, по начальному же конусу заготовки в инструментальном зацеплении.
Вот ещё:
Разве это не «лысенковщина» в механике?
Самое интересное, что сферическая эвольвента «фоново» присутствует в тех результатах, что приведены в книгах вышеупомянутых товарищей. Об этом можно судить по «пёрлу» из монографии тов. Литвина:
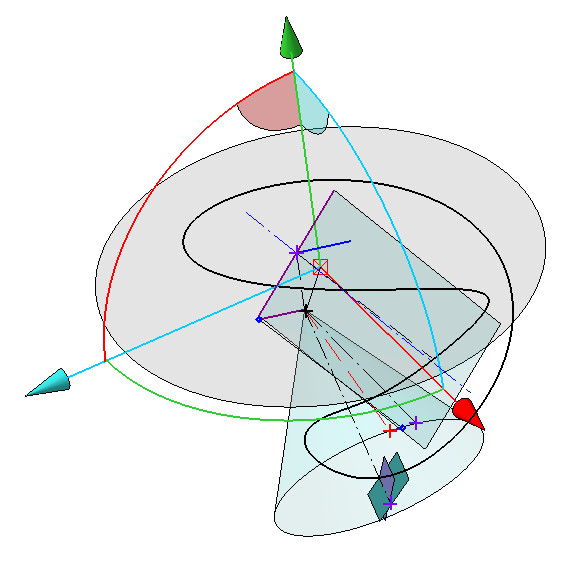
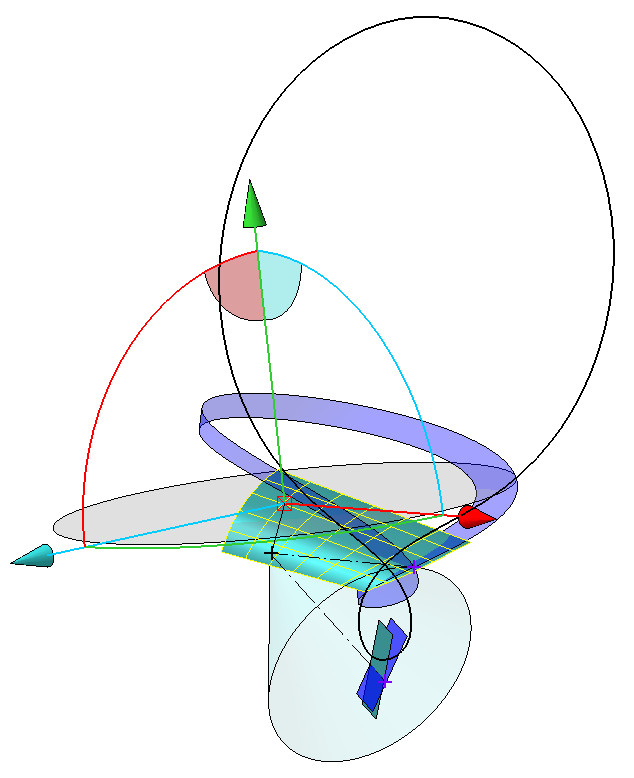
Между прочим, чтобы получить этот бред про «октоидальное зацепление», нужно было получить модель процесса зубострогания конического зубчатого колеса. И вполне очевидный частный случай параметров такой модели будет иметь результатом поверхность зуба, образованную семейством самых настоящих сферических эвольвент. В общем же случае поверхность зуба будет образована пространственными кривыми, которые можно назвать сфероидными, т.к. они будут переменного радиуса сферы из-за переменного же станочного угла зацепления.
Получается, «только лишь немногие могут видеть сферическую эвольвенту».
А «октоидальное зацепление», вероятно, явилось прародителем современного: «сферический конь в вакууме»! Это - наглядный пример игр с «чистой математикой» без опоры на физическую реальность.
Любому трезвому пролетарию-станочнику понятно, что реальное зацепление конических зубчатых колёс происходит только в некоторой окрестности оси зацепления, а «восьмёрка» - продукт недоразвитого пространственного воображения разухарившихся математиков. Да и то: только при целочисленном станочном передаточном отношении.
P.S.: подробный разбор моделирования геометрии и кинематики процесса зубострогания конических зубчатых колёс будет размещён на Дзен-канале «Добро» на вентилятор».