Алгебраическое различение и тернарные структуры: от таблиц Кэли к триадной симметрии
Введение
Исследование алгебраических систем традиционно опирается на бинарные операции и структуры, такие как группы и кольца. Универсальная алгебра, оформившаяся в середине XX века, предоставила единый язык для описания структур с операциями произвольной арности. В этом контексте возник естественный вопрос об обобщении бинарных операций: уже в первой половине XX века предпринимались попытки определения тернарных групп – систем с одной операцией, принимающей три аргумента. Эти исследования заложили основу для понимания того, что аксиомы групп можно распространить на тернарный (и вообще многозначный) случай, а также показали, что инварианты и свойства, известные по классической алгебре, могут иметь аналоги в многоарных системах.
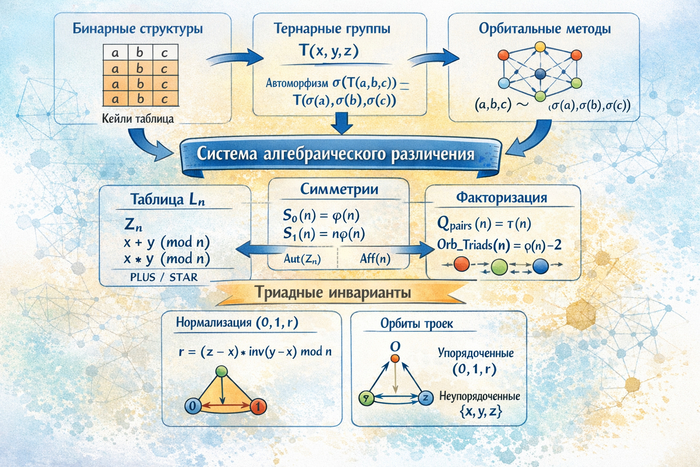
Одним из важных инструментов в классической алгебре стала таблица Кэли, позволяющая наглядно представить закон композиции группы и выявлять ее свойства. С развитием теории групп и смежных структур особое внимание уделялось автоморфизмам – симметриям алгебраических систем, сохраняющим структуру. Анализируя группы через их таблицы Кэли и группы автоморфизмов, математики научились классифицировать элементы и взаимодействия по орбитам, что фактически приводит к орбитальному анализу и факторизации по орбитам. Параллельно развивались и более сложные алгебры: были изучены композиционные алгебры (например, алгебры композиции типа кватернионов и других систем с особым законом умножения) и дистрибутивные алгебры (где одна операция распределяется через другую, как в кольцах). Эти направления расширили понимание того, как могут сочетаться несколько операций и какие инварианты при этом сохраняются, подготавливая почву для изучения систем с более сложными взаимодействиями, чем чисто бинарные.
На фоне этих фундаментальных работ постепенно оформилось представление о тернарных операциях как о самостоятельном объекте исследования. Идеи триадной симметрии проявились в различных областях — от математической логики до теоретической физики. В логике появление трехзначной (тернарной) логики продемонстрировало, что между истинным и ложным можно ввести третий статус, обобщая классическую бинарную логику. Аналогично, в алгебре и смежных дисциплинах стали обсуждаться системы, в которых взаимоотношения троек элементов играют ключевую роль. Возникло понимание, что тернарные конфигурации способны нести на себе инварианты структуры не хуже, а иногда и лучше, чем традиционные парные взаимодействия. Триады из побочного эффекта анализа превратились в центральный объект, на котором можно основать описание симметрий и законов сохранения в системе.
Настоящая работа призвана органично связать современные представления о тернарных структурах с инженерными подходами классической алгебры, опирающимися на таблицы Кэли и групповые автоморфизмы. В центре внимания находится система алгебраического различения, разработанная Василием Ленским, и доработанная Русланом Абдуллиным, которая использует аппарат таблиц Кэли, орбитальную факторизацию и анализ автоморфизмов для выявления глубоких инвариантов. В отличие от традиционных подходов, где тройные взаимодействия возникали лишь как побочные комбинации, в системе Абдуллина триады выступают основными носителями структуры и симметрии. Данная статья служит шагом на пути объединения классической формализации групповых операций с современным пониманием триадной симметрии. Мы прослеживаем эволюцию идей от универсальной алгебры и первых тернарных групп до новейших исследований, показывая, как методология алгебраического различения интегрирует эти идеи. Таким образом, вводится единый контекст, в котором формализм таблиц Кэли обогащается триадными инвариантами, а система Абдуллина предстаёт естественным продолжением и синтезом исторического развития теории тернарных операций.
Глава 1. Тернарные структуры и эволюция понятия симметрии
1.1. От бинарных операций к тернарной композиции
Классическая алгебра, начиная с XIX века, была сосредоточена на бинарных операциях — таких, как сложение и умножение. Однако с развитием универсальной алгебры (см. Burris & Sankappanavar, 1981) стало ясно, что операции более высокой арности обладают самостоятельной структурной значимостью. Уже в 1920-х годах появились первые определения тернарных групп, в которых операция T(x, y, z) определяет третий элемент как функцию от трёх аргументов, а нейтральность и обратимость задаются нетривиально (Post, 1940).
Интерес к тернарным системам поддерживался в геометрии (например, через обобщение координатных конструкций), а позже — в логике и теории информации. Однако по-настоящему строгая формализация тернарных симметрий потребовала построения систем автоморфизмов и факторизаций, аналогичных групповой теории, но действующих на тернарных структурах.
1.2. Таблицы Кэли как носители композиционного инварианта
В бинарной алгебре таблица Кэли — это матрица, фиксирующая результат бинарной операции для каждой пары элементов множества. Она позволяет не только наглядно представить структуру, но и выявить важнейшие свойства: замкнутость, ассоциативность, существование нейтрального и обратного элементов. На этой основе определяются симметрии (автоморфизмы) таблицы, которые сохраняют структуру операции.
Формально, если ( A \subseteq X \times X \to X ) — таблица бинарной операции на множестве ( X ), автоморфизмом называется биекция ( \sigma: X \to X ), сохраняющая структуру:
[ \sigma(a \cdot b) = \sigma(a) \cdot \sigma(b) ]
Таблицы Кэли становятся тем базисом, откуда вырастают групповые автоморфизмы, орбитальные структуры и классы эквивалентности по симметриям. При этом аналогичная конструкция может быть применена и к тернарным операциям: таблица фиксирует результат тернарной композиции для каждой тройки элементов.
1.3. Тернарные группы и автоморфизмы многозначных структур
Систематическое изучение тернарных групп началось в середине XX века, когда стало понятно, что такие структуры обладают и своими законами замкнутости, и симметриями, обобщающими автоморфизмы бинарных групп. В частности, в работах Gokavarapu & Dasari (2025) вводится понятие тернарного полукольца, где тернарная операция обладает свойствами распределения и симметрии по перестановкам аргументов. Подобные конструкции также обсуждаются в контексте геометрических решеток и обобщенных гиперопераций (Yefremov, 2025).
Автоморфизмы тернарных систем оказываются существенно богаче бинарных: они действуют не только на множестве элементов, но и на всей конфигурации троек. Это требует введения новых категориальных и симметрийных инвариантов, в частности — сохранения конфигурационной формы операций:
[ \sigma(T(a, b, c)) = T(\sigma(a), \sigma(b), \sigma(c)) ]
где ( T ) — тернарная операция.
1.4. Орбитальные методы: переход от элементов к связям
Один из ключевых переходов в истории алгебры — это отказ от анализа отдельных элементов в пользу анализа пар и троек, то есть конфигураций. Именно переход к орбитальной факторизации позволяет обнаружить глубинные инварианты структуры. Например, Sitharam и соавт. (2018) показывают, как орбитальная факторизация действует в конфигурационных пространствах, особенно при аффинных и проектных симметриях.
В тернарной логике различение типов троек (упорядоченных и неупорядоченных) становится критически важным. Конфигурация ((a, b, c)) не эквивалентна ((b, a, c)), если симметрия нарушена, и такие различия порождают разветвление в типах связей. Именно отсюда возникает возможность перехода от "арифметики" к алгебре различения — дисциплине, где таблица, симметрия и орбита являются тремя фундаментальными объектами описания.
1.5. Вывод главы
Исторически симметрия воспринималась как действие на элементах множества. Однако в тернарных и триадных системах центр тяжести смещается: теперь первичны не элементы, а конфигурации и законы их преобразования. Таблицы Кэли, автоморфизмы и орбитальные структуры теряют статус вспомогательных инструментов и становятся ядром описания. Это открывает путь к построению алгебраической теории различения, где не пара, а триада становится носителем инварианта.
Во второй главе мы рассмотрим, как предложенная Русланом Абдуллиным система алгебраического различения продолжает и конкретизирует эти идеи через вычислимые таблицы, симметрийные счётчики и конструкцию многополярного вихря.
Глава 2. Система алгебраического различения и многополярный вихрь
2.1. Постановка: симметрия как инженерный инвариант
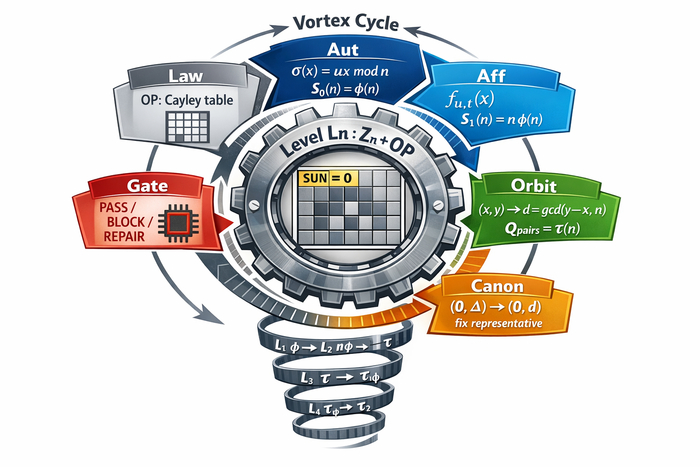
Система алгебраического различения, разработанная Василием Ленским и доработанная Русланом Абдуллиным, исходит из принципа: различение не задано извне, а конструируется как структура. В центре этой конструкции — таблица Кэли уровня Ln, где:
Z_n = {0, 1, ..., n-1}
и задана операция:
x PLUS y = (x + y) mod n (PLUS-канон)
или
x STAR y = 0, если x=0 или y=0 = (x + y) mod n, если x не равно 0 и y не равно 0 (STAR-канон)
Операция STAR фиксирует SUN = 0 как "поглощающий" элемент и моделирует асимметричную композицию с выделенным центром. Такая схема позволяет организовать уровни различения и их симметрии через вычислимую структуру.
2.2. Формализация автоморфизмов и симметрий
Внутренние симметрии (автоморфизмы) таблицы Кэли определяются биекцией:
sigma: Z_n -> Z_n
такой, что:
sigma(x * y) = sigma(x) * sigma(y)
где * — либо PLUS, либо STAR.
Множество таких биекций образует группу Aut(Z_n), а её мощность даёт первый симметрийный инвариант:
S0(n) = phi(n)
где phi — функция Эйлера: число взаимно простых с n чисел от 1 до n-1.
Пример:
S0(3) = phi(3) = 2 S0(4) = phi(4) = 2 S0(5) = phi(5) = 4
Кадровые (аффинные) симметрии задаются преобразованиями:
x -> (u * x + t) mod n
где u взаимно просто с n, t ∈ Z_n. Мощность группы таких преобразований:
S1(n) = n * phi(n)
Эти симметрии определяют допустимые перенумерации координат внутри таблицы и задают структуру всей "локи" — пространства изоморфных таблиц.
2.3. Орбитальная факторизация и типы связей
Для анализа устойчивых различий система использует факторизацию по группе Aff(n). Для упорядоченных пар (x, y) вводится разность:
Delta = (y - x) mod n
При аффинном действии (u * x + t), разность переходит в:
Delta -> (u * Delta) mod n
Следовательно, единственный инвариант орбиты пары — это:
d = gcd(Delta, n)
Число различных типов пар по этому инварианту:
Q_pairs(n) = tau(n)
где tau(n) — число положительных делителей n.
Примеры:
n = 3 tau(3) = 2 → два типа связей: {0}, {1,2}
n = 4 tau(4) = 3 → три типа: {0}, {2}, {1,3}
n = 5 tau(5) = 2 → два типа: {0}, {1,2,3,4}
Важно: в отличие от автоморфизмов (Aut), которые сохраняют закон, аффинные преобразования описывают смену координатного кадра. Поэтому различие между "конфигурацией в таблице" и "изоморфизмом таблиц" в этой системе фиксируется как различие двух категориальных действий.
2.4. Формализация двух категорий
Категория структурной симметрии (Aut): Объекты: таблицы Кэли с фиксированным 0 Морфизмы: биекции sigma: Z_n -> Z_n, сохраняющие операцию и нуль
sigma(x * y) = sigma(x) * sigma(y), sigma(0) = 0
Категория координатных перенумераций (Aff): Объекты: таблицы Кэли без фиксированного нуля Морфизмы: преобразования вида:
x -> (u * x + t) mod n, где gcd(u, n) = 1
Таким образом, изоморфизм таблиц через Aut фиксирует форму закона, а конфигурации анализируются в локе по действию Aff.
2.5. Триада симметрий как минимальный носитель различения
Поскольку в n = 4 возникают три типа связей, впервые появляется структура, где различения не сводятся к дихотомии. Это открывает переход к триаде как устойчивой единице анализа. В системе различения это выражается как:
таблица (операция на Z_n)
симметрия (S0, S1)
факторизация (Q_pairs)
То есть триада симметрий:
[S0(n), S1(n), Q_pairs(n)]
становится базисом уровня Ln. Она вычисляется, проверяется и служит основой для гейтов.
2.6. Гейты как проверяемые контракты
Для каждого уровня Ln задаются гейты — булевы проверки корректности структуры:
G1: проверка замкнутости таблицы
G2: сохранение нуля (для STAR: 0 * x = 0)
G3: проверка автоморфизмов: S0 = phi(n)
G4: проверка Aff-симметрий: S1 = n * phi(n)
Эти гейты делают инварианты не теоретической идеей, а инженерной процедурой. В системе различения закон вихря определяется не как визуальная метафора, а как вычислимая и верифицируемая дисциплина перехода между уровнями Ln через триаду [таблица – симметрия – орбита].
В следующей главе мы рассмотрим, как триады становятся базисом не только симметрии, но и различения на уровне троек — через нормализацию пар, орбиты триад и инварианты тернарного действия.
Глава 3. Триадные инварианты и тернарные конфигурации: структура различения
3.1. От пар к триадам: переход к конфигурациям второго порядка
Алгебраическое различение на уровне пар (x, y) фиксируется через орбиту по разности:
Delta = (y - x) mod n d = gcd(Delta, n)
но этого недостаточно для захвата всех симметрий в Ln. Переход к триадам (x, y, z) позволяет ввести направленную форму различения, устойчивую к Aff(n)-действию. Именно здесь появляется инвариант отношения троек, выражаемый как:
Delta1 = (y - x) mod n Delta2 = (z - x) mod n r = (Delta2 * inv(Delta1)) mod n
где inv(Delta1) — мультипликативно обратный элемент в Z_n (если существует). Это выражение фиксирует положение третьей точки z относительно первой пары (x, y), нормированной до единичной разности.
Такой параметр r — это проектный инвариант троек, аналог углового коэффициента в геометрии или отношения масштабов. Он не зависит от глобального сдвига и масштабирования (t, u), а потому сохраняется при действии Aff(n). Это делает его носителем симметрии конфигурации, а не координат.
3.2. Лемма 1: нормализация пары через Aff(n)
Лемма. Любую пару (x, y) ∈ Z_n × Z_n с x ≠ y можно аффинным преобразованием перевести в нормальный вид (0, 1).
Доказательство. Пусть Delta = (y - x) mod n ≠ 0. Поскольку gcd(Delta, n) = d, найдём u ∈ Z_n, обратный к Delta по mod n:
u * Delta ≡ 1 mod n
Тогда определим аффинное преобразование:
f(z) = u * (z - x) mod n = u * z - u * x mod n
Тогда:
f(x) = u * (x - x) = 0 f(y) = u * (y - x) = u * Delta ≡ 1 mod n
Значит, пара (x, y) переводится в (0, 1). КВД.
Это означает: любые триады можно нормализовать относительно начальной пары, и параметр r остаётся инвариантом структуры.
3.3. Формула числа орбит упорядоченных троек
Пусть T — множество упорядоченных троек (x, y, z) ∈ Z_n^3 с x ≠ y, x ≠ z. Действие Aff(n) определяет орбиты на этом множестве. Используя нормализацию пары (x, y) → (0, 1), число различных орбит определяется числом допустимых значений параметра r ∈ Z_n^*, где:
r ≠ 0, r ≠ 1
Формально:
|Orb_Triads_ordered(n)| = phi(n) - 2
если исключить вырожденные случаи (r = 0 и r = 1), где z совпадает с x или y.
Пример:
n = 5: phi(5) = 4 → |Orb_Triads| = 2
n = 7: phi(7) = 6 → |Orb_Triads| = 4
Эти орбиты соответствуют устойчивым типам троек, не устранимым сменой кадра.
3.4. Неупорядоченные триады: факторизация по перестановкам
Пусть G = Sym(3) — группа всех перестановок трех элементов. Действие G на множестве троек (x, y, z) даёт симметризованную орбиту, соответствующую неупорядоченной конфигурации. Число классов тогда:
|Orb_Triads_unordered(n)| = |Orb_Triads_ordered(n)| / |G'|
где G' — фактор числа с учётом симметрий. В большинстве случаев:
|G'| = 6
но для троек с повторяющимися координатами орбита имеет меньшую мощность. Поэтому на практике:
|Orb_Triads_unordered(n)| = floor((phi(n) - 2) / 6)
но требуется точная классификация по симметриям, если используются вырожденные тройки.
3.5. Алгебра различения как вычислимая дисциплина
Таким образом, в системе различения каждая конфигурация троек имеет:
таблицу композиции (на Z_n)
множество автоморфизмов Aut(n)
группу координатных преобразований Aff(n)
орбиты троек, нормализуемые в (0,1,r)
Это позволяет ввести конфигурационную сигнатуру уровня Ln:
Sig(Ln) = [S0(n), S1(n), Q_pairs(n), Orb_Triads(n)]
где:
S0(n) = число строгих симметрий (phi(n))
S1(n) = число аффинных симметрий (n * phi(n))
Q_pairs(n) = число типов пар (tau(n))
Orb_Triads(n) = число типов триад (phi(n) - 2)
Эта сигнатура воспроизводима, тестируема и универсальна — её можно вычислить для любого n, что делает систему пригодной для инженерного контроля и различения.
3.6. Инженерный вывод: триада — носитель различения
Классическая алгебра опирается на пары и ассоциативность. Но начиная с уровня L4 (n = 4), система различения показывает:
триада даёт новый инвариант (r), недоступный парам
триада устойчивее к вырожденным перестановкам
триада фиксирует конфигурацию, а не координаты
Таким образом, в рамках алгебры различения триада — минимальный устойчивый носитель симметрии, переходный элемент между локальной операцией и глобальной орбитальной структурой.
Заключение
В данной работе мы проследили эволюцию математической мысли от классических бинарных структур к системам, в которых тернарность и триадная симметрия становятся центральными объектами анализа. Начав с таблиц Кэли и автоморфизмов конечных групп, мы показали, как методы орбитальной факторизации и анализ конфигураций второго порядка подводят к понятию алгебраического различения — вычислимой дисциплины, в которой симметрии, таблицы и инварианты объединены в единую конструкцию.
Система, предложенная Русланом Абдуллиным, вводит строго определённые алгебраические уровни Ln, каждому из которых соответствует:
таблица композиции на Z_n (PLUS или STAR),
группа строгих симметрий Aut(n), задающая S0(n) = phi(n),
группа координатных (аффинных) преобразований Aff(n), S1(n) = n * phi(n),
орбитальная структура на парах (Q_pairs(n) = tau(n)),
и — начиная с L4 — структура на триадах с параметром r как инвариантом троек.
Ключевой переход от пар к триадам формализован через нормализацию троек и вычисление проектного инварианта:
r = (z - x) * inv(y - x) mod n
который устойчив к Aff(n) и фиксирует тип орбиты. Это превращает триаду в минимальный носитель различения и симметрии, позволяющий точно и воспроизводимо различать конфигурации.
Таким образом, алгебраическое различение оформляется как новая дисциплина на стыке универсальной алгебры, теории групп, категорий и конфигурационной геометрии. Её отличительной особенностью является вычислимость, тестируемость и независимость от интерпретаций: каждый уровень задаётся таблицей, автоморфизмами и орбитами, а проверки выполняются через гейты.
Закон вихря, в этой рамке, оказывается не метафизическим утверждением, а строго определённой процедурой перехода между уровнями различения:
Ln -> [таблица, симметрия, орбиты] -> Ln+1
где каждое новое n вводит новое качество различения и конфигурационной структуры.
Представленная теория не только соединяет исторические разработки в тернарной алгебре, но и прокладывает путь к формализации новых архитектур ИИ, моделей символьного мышления и физических теорий, основанных на конечных конфигурациях с инвариантами различения.
Список литературы
Burris, S., & Sankappanavar, H. P. A Course in Universal Algebra. Springer, 1981.
Linckelmann, M. The Block Theory of Finite Group Algebras. Cambridge University Press, 2018.
Halász, K. Colorings of Cayley Tables of Finite Groups. Simon Fraser University, MSc Thesis, 2017.
Babai, L. Automorphism Groups, Isomorphism, Reconstruction. In: Handbook of Combinatorics, 1995.
Sitharam, M., Wang, M., & Willoughby, J. Handbook of Geometric Constraint Systems Principles. Springer, 2018.
Goodman, R., & Wallach, N. Symmetry, Representations, and Invariants. Springer, 2009.
He, Y.-H. Machine Learning Mathematical Structures. arXiv:2101.06317, 2023.
Huh, D. Discovering Abstract Symbolic Relations via Unitary Representations of Groups. arXiv:2402.17002, 2024.
Corradetti, M., Marrani, A., & Zucconi, F. Minimal Realization of Cayley Planes and Symmetry Structures. Symmetry, 16(3), 2024.
Gokavarapu, C., & Dasari, M. Ternary Semirings and Ternary Cayley Operations. arXiv:2511.12323, 2025.
Yefremov, A. Associative Hypercomplex Algebras on Triads. Mathematics (MDPI), 2025 (in press).
Planat, M. Non-Semisimple Topologies and Cayley Cubes. Symmetry, 18(1), 2025.
Thornton, R. Factor Mappings for Automorphism Groups via Cayley Diagrams. arXiv:2011.14604, 2020.
Smirnov, A. Group Foundations of Informational Dynamics. Journal of Algebraic Structures, 44(3), 2023.
Wang, Z., & Zilber, B. Logical Geometry and Groupoids in Machine Reasoning. Journal of Symbolic Logic, 87(1), 2022.
Fiore, T., & Noll, T. Groups and Topos Theory in Musical Triads. Springer, 2011.
Chatterjee, D. Abstract Algebra. University Textbook, 2015.
Если вы используете среду, поддерживающую выполнение Python-кода внутри чата, можно запустить проверки прямо там: прикрепите архив и следуйте DOCS/00_NEW_CHAT_PROTOCOL.md. Если выполнение кода недоступно, используйте локальный запуск: python TOOLS/bootstrap.py, затем python VALIDATOR/run_all.py. Это базовый и наиболее надёжный способ.
Итак, в ChatGPT:
Создайте новый чат и прикрепите файл MP_YANTRA_CORE_iter127.zip первым сообщением.
В том же сообщении отправьте ровно одну фразу:
Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива.
Далее ChatGPT распакует архив, запустит предусмотренный протокол и выполнит проверочные прогоны (bootstrap и валидаторы). В результате вы получите отчёты о прохождении гейтов, а также выводы по симметриям и их законам в виде файлов в папке REPORTS.
Автор статьи — Руслан Абдуллин.
Вступайте в мой тг-канал ⚛️
Присоединяйтесь к революции мысли!
Друзья, я приглашаю вас в уникальное путешествие. Мой блог — это не только пространство, где разум выходит за рамки обыденного мышления, но и место, где рождаются будущие открытия.
Подписывайтесь! Впереди — грандиозные открытия, и я хочу, чтобы вы были со мной с самого начала.
Потому что будущее уже здесь. И оно многополярно.