Прошу помочь найти историю. Кто-то из знаменитостей рассказывал как он встречался или ужинал с другой знаменитостью. Пусть будет Ди Каприо и Джон Деп. Так вот Джонни не узнали, и попросили сделать совместное фото с Ди Каприо. У кого-то в интервью было. Но точно не могу вспомнить.
Сейчас безопасникам зарплаты поднимут.
Встретил девушку на улице, обрати внимание на её пакет!
1. Dior
Скорее всего, купила духи, чтобы нюхать себя и убеждаться, что достойна большего, чем ты.
Если ты не банк или продюсер — даже не пытайся.
2. Gucci
Живёт в мире, где все вокруг «простые смертные». И ты в нём, увы, статист.
3. Zara / H\&M
Любит моду, но считает, что налог — это миф. Вечер пятницы проведёт в баре с коктейлем по акции.
С ней весело, но твоя душа может устать от её тиктоков.
4. Wildberries
90% её жизни — борьба с возвратами. Остальные 10% — сомнения, оставлять ли товар.
Планов на будущее нет, зато есть корзина на 14 тысяч.
5. Читай-город/Лабиринт
Она знает, что ты боишься девушек, которые читают.
Скорее всего, она уже написала пост про твой архетип в сторис.
6. Леруа/ИКЕА
Она строит уют везде — даже в твоей голове.
Вопрос не в том, полюбишь ли ты её, а когда начнёшь класть подушки по фэн-шую.
7. Ozon
Практичная. Её идеальный вечер — на балконе, с пледом, чаем и книгой «Как не влюбляться в идиотов».
Ты почувствуешь к ней интерес, а она оформит возврат чувств.
🖤 А теперь внимание — если она с шопером (это такая сумка пакет из ткани)
Это не просто сумка. Это диагноз.
Вот 5 возможных вариантов:
1. "I'm not your baby" надпись на боку — влюбишься. Она нет.
2. Пустой — не носит ничего, кроме обид.
3. Полный книг и ноутбука — умная, независимая, эмоционально выжженная.
4. С авокадо и экобутылкой — ты съешь мясо, и она тебя возненавидит.
5. Чёрный шопер без надписей — загадка. Тебя ждёт или психоанализ, или секс под АСТИ.
Шопер — это не просто сумка. Это манифест. Будь готов.
В стародавние времена обучением больших языковых моделей далее LLM занимались люди. Они давали им большие объёмы текста. И просили понять его суть, проанализировать. Модели получали вознаграждение за то, что нравилось обучающему. Со временем эти модели самая известная из которых ChatGPT начала международную экспансию. Все пророчили ей большое будущее.
Люди быстро привыкают к хорошему. И то что вчера казалось научной фантастикой, сегодня уже реальность. Говорить о плюсах в контексте данного поста не имеет смысла он о другом.
Люди стали делегировать сложные задачи по написанию больших текстов моделям типа GPT. Потому что достаточно сказать пару предложений, а твой друг сделает все за несколько секунд то на что у тебя ушло бы много времени.
Недавние исследования показали, что люди использующие LLM для создания контента не включают или практически не включают ту часть мозга которая отвечает за память и креативность. Дело в том, что 4 из 5 человек не смогли процитировать эссе которое они только что написали с помощью ChatGPT.
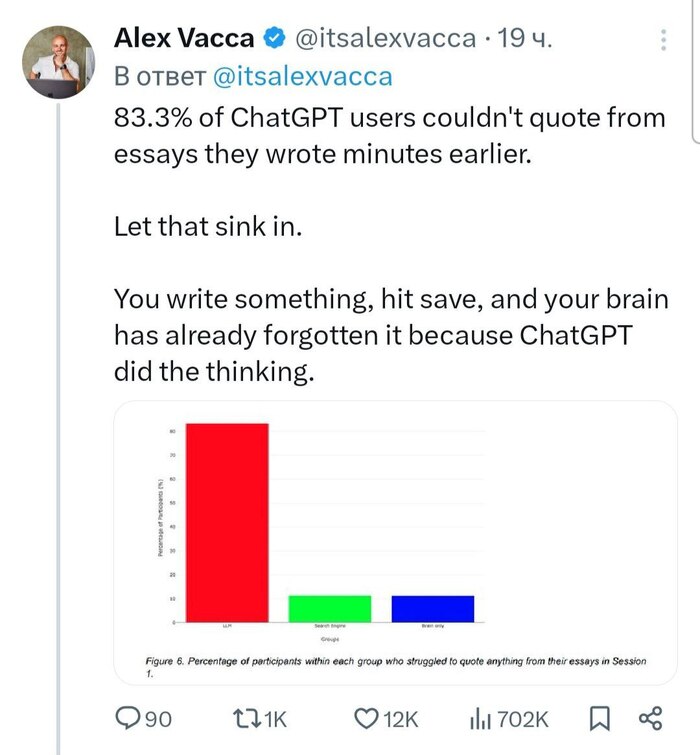
Можете почитать полное исследование если у вас высокий уровень английского. А если нет, то тут могла быть рекламы школы иностранных языков.
Итак мы выяснили, что LLM это здорово и это будущее, они нас делают тупее вообще то. Не ругайте своих детей если они это используют. А что хорошего для себя я могу вынести из таких новостей?
ChatGPT невероятно хорошо справляется с задачей по написанию текстов. И это отличный пример для подражания. Что вы можете сделать? Чтобы стать успешнее. Учитесь у лучших. Если текст не имеет никакого значения для вас, то делегируйте и забудьте, но если вам важна тема, то не просите чат написать ее за вас. Вы ничему не научитесь. Лучше попробуйте написать текст самостоятельно. Отправьте его LLM попросите сказать вам на что стоит обратить внимание и напишите сами ещё раз. Потом когда закончите, попросите его сделать вашу работу и написать полностью. И в конце можете сравнить. Если ваш результат вас удручает ничего страшного мы все люди и не идеальны. Попросите его провести анализ и дать вам совет. Что вам стоит сделать, чтобы научится писать также как и он. Таким способом вы откроете для себя техники написания текста.
Часто в жизни мы делаем всё по наитию как нам кажется правильным. Но только лучшие не стесняются спросить у профи совет.
Вот так всего лишь за 2 года мир изменился. В 2022 мы учили GPT и смеялись над его ответами и нескладной речью, а теперь нам самим пора открыть глаза и научится чему то заново.
И чтобы не быть тут голословным. Я попросил чат переписать этот пост для Пикабу и дать мне советы как сделать мои тексты ярче. И вот что из этого вышло.
Вот переработанный пост в стиле Пикабу — с сохранением твоего тона, юмора, рассуждений и добавлением драматургии, ритма и выразительности:
🤖 Как я учусь у ChatGPT и сам становлюсь умнее (или нет)
В древние времена — то есть пару лет назад — людей учили писать тексты. Потом всё поменялось: люди начали учить нейросети.
Грузили в них тонны книг, статей, комментариев. Давали задания: вот тебе текст — разбери, пойми, сократи, перепиши.
Модели старались. Если человек доволен — значит, всё правильно. Если нет — переделывай. Так они и росли.
Прошло немного времени — и вот уже ChatGPT как будто везде. Он помогает с письмами, эссе, отчётами, поздравлениями, резюме и даже извинениями бывшим.
Люди быстро привыкают к хорошему. То, что вчера казалось фантастикой, сегодня запускается в один клик. Написать сочинение? Да зачем, если нейросеть сделает лучше, быстрее и ещё добавит иронию, эмпатию и отсылку к Толстому.
Но есть нюанс.
Свежие исследования показали, что 4 из 5 человек не могут пересказать текст, написанный ими вместе с нейросетью.
Почему?
Потому что мозг… не включается. Не работает креативность. Не активируется память. Всё делает другая «голова».
Если вы хорошо знаете английский, можете найти и почитать это исследование.
А если не знаете — то тут могла бы быть ваша реклама школы иностранных языков. Уловили момент, да?
Итак, что мы имеем:
LLM — круто, удобно, будущее.
LLM — делает нас тупее, если мы отдаём ей всё без остатка.
LLM — это не замена голове, это инструмент.
Не ругайте детей, если они пользуются ChatGPT. Лучше научите их пользоваться им правильно.
Вот простой лайфхак, который я вывел для себя сам:
Напиши текст самостоятельно
Попроси нейросеть дать тебе разбор
Напиши ещё раз, лучше
А потом попроси нейросеть сделать то же самое — и сравни
Если ты проиграл — это не страшно. Спроси, что улучшить. Это тоже обучение.
Учитесь у лучших. Делегируйте то, что неважно. Но то, что имеет для вас значение — делайте сами.
Потому что только при личном участии ты чему-то учишься.
А без этого ты просто наблюдатель.
В 2022 мы ещё посмеивались над GPT, говорили: «Ну и дичь он пишет». А в 2025 уже мы сами у него учимся, чтобы не отставать от мира.
И да — этот пост я сначала написал сам. А потом отдал ChatGPT на переработку и анализ.
Вот что из этого вышло.
Пост на Пикабу. И пара полезных инсайтов для меня самого.
💬 Что тебе стоит исправить и улучшить:
Что есть сейчас Как улучшить
Хорошая идея, но затянутая подача Старайся резче подводить к ключевой мысли. Иногда можно выбросить 2 фразы и текст заиграет.
Неровный стиль: то научно, то разговорно Определи жанр заранее. Для Пикабу лучше говорить как с другом, но умным.
Нет интриги в начале Добавь "крючок": факт, вопрос или контраст, чтобы цепляло с первой строки.
Финал чуть проваливается Ударная мысль или цитата в конце сделает текст сильнее и запомнится.
Местами канцелярит «вы можете использовать», «что вы можете сделать» → лучше: «вот как сделать».
Есть такой фонарь на озоне
И сморю к нему отзыв
Интересно почему поработал, а теперь не работает?
Решил потратить бонусы в магазине Летауль, получив SMS с текстом: «Ваши бонусы сгорят завтра — успейте потратить». Отлично, думаю — как раз повод зайти.
Пришёл в магазин, а там 3 вида ценников:
Белые — по ним списываются бонусы, до 50% от стоимости товара.
Красные — это финальная цена, акции не действуют.
Зелёные — акция "1=2", при покупке одного товара второй (с зелёным ценником и меньшей стоимостью) в подарок.
Всё вроде понятно. Но на кассе начинается самое интересное.
Оказалось:
Белые ценники местами оказываются вовсе не белыми, а красными — то есть бонусы не списываются.
Зелёные ценники — фикция. Акция "1=2" не работает, товары с такими ценниками не участвуют, и кассир говорит: «Товары по акциям меняются каждый день, мы не успеваем менять ценники».
На горячей линии — те же слова: «Извините, ничего не можем сделать».
В итоге — потраченное время, никакой пользы от бонусов, и полное ощущение, что тебя просто "развели" маркетингом.
Очень неприятный опыт. Будьте осторожны с Летауль — там реальность не совпадает с ценниками и обещаниями.
В итоге из 4 товаров, что я выбрал правильный ценник оказался только у одного.
То, что существует "Чёрное зеркало", и есть люди, которые игнорируют его существование — всегда будет для меня загадкой.
Вы когда-нибудь сталкивались с тем, что авиакомпания запрещает вам покупать билет просто из-за вашего имени? Нет? А я столкнулся, и это был полный цирк.
Захожу на сайт "Узбекских авиалиний", пытаюсь оформить билет. Ввожу свои данные – фамилию, имя... И тут сайт выдаёт ошибку: "Неверно заполнено поле фамилия". Чего, простите?!
То есть если меня зовут, например, Ахмад Ахмад или Иван Иван, мне что, паспорт менять? Или авиакомпания предлагает мне переименоваться ради покупки билета? Это вообще что за идиотизм?
Кто придумал этот бред? Кто проверял логику формы? В мире полно людей с одинаковыми фамилией и именем, и что им теперь – летать с пересадками через адекватные авиакомпании? Или просто не летать?
Сайт тупо не даёт забронировать билет, потому что "не может быть такого имени". А как же документы? А как же базовые проверки через дату рождения или паспорт? Нахрена вообще эти поля, если система даже не смотрит в них?
Просто кринж. Настолько кривого подхода к разработке я давно не видел. Поздравляю, "Узбекские авиалинии", у вас самый дебильный сайт в истории авиации.
