Где то я уже это видел
Николас Пиццолатто родился в 1975 году в Новом Орлеане, штат Луизиана
Собснна это всё не придумано им, а взято из своего детства - сантерия, жёлтый король, каркоза
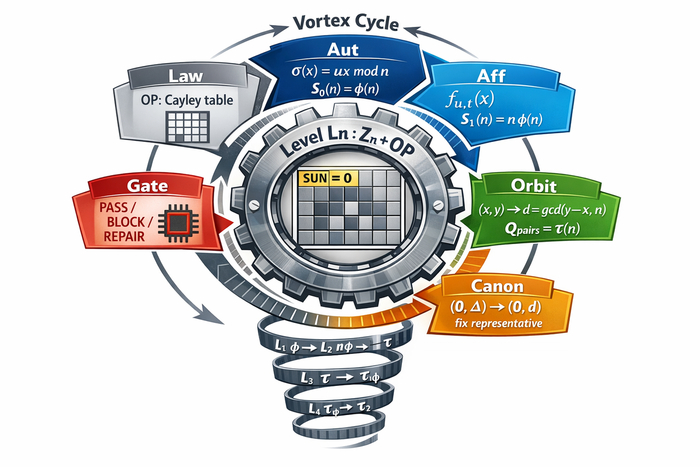
Формализация закона вихря: таблицы Кэли, симметрии и многополярность как алгебраическая система различения
Глава 1. Базовая конструкция уровня Ln: таблица Кэли, симметрии закона и «вихрь» как вычислимая процедура
1.1. Цель и метод: от риторики к проверяемому вычислению
Я трактую «закон вихря» не в качестве метафоры, а как строго формализованный, воспроизводимый протокол, регулирующий переход между уровнями различения. В рамках этого протокола предмет дискуссии может составлять исключительно процесс вычисления, поскольку каждый шаг подлежит проверке посредством инвариантов и гейтов.
Содержание закона вихря в минимальном виде:
задать конечное множество состояний уровня Ln;
задать бинарный закон композиции (операцию), полностью определяемый таблицей Кэли;
вычислить две группы преобразований: строгие симметрии закона (автоморфизмы), кадровые (аффинные) преобразования, отвечающие за смену координат/кадра;
факторизовать конфигурации (пары, затем тройки) по действию кадровой группы;
закрепить вычислимые счётчики уровня и гейты, которые запрещают «съезжать» с канона.
Далее в главе я даю точные определения и вывожу базовые формулы счётчиков, на которых держится вся инженерная дисциплина.
1.2. Уровень Ln: множество состояний
Пусть n >= 1. Уровень Ln задаётся конечным множеством состояний
Z_n = {0,1,...,n-1}.
Все дальнейшие операции и равенства понимаются по модулю n.
1.3. Таблица Кэли как полное задание закона
Пусть OP — бинарная операция
OP: Z_n x Z_n -> Z_n.
Таблица Кэли операции OP — это полное задание значений OP(x,y) для всех (x,y) из Z_n x Z_n.
Важно подчеркнуть, что таблица Кэли — это не декоративное оформление или иллюстративный материал, а полноценная форма спецификации закона. Если закон не задан посредством таблицы Кэли (либо эквивалентным правилом, которое однозначно позволяет построить такую таблицу), то любые дальнейшие рассуждения о симметриях, инвариантах и факторизациях утрачивают строгую обоснованность и перестают иметь чёткий математический смысл.
1.4. Два канона операции: PLUS и STAR(SUN)
1.4.1. PLUS-канон
Определим:
x PLUS y = (x + y) mod n.
Это каноническая циклическая операция уровня Ln.
1.4.2. STAR-канон с выделенным элементом SUN
Зафиксируем SUN = 0 и определим:
x STAR y = 0, если x=0 или y=0, x STAR y = (x + y) mod n, если x не равно 0 и y не равно 0.
Здесь SUN работает как «поглощающий» элемент: любое умножение STAR с участием SUN даёт SUN. В инженерном языке это не «верование», а фиксация режима, где нулевое состояние обладает выделенной ролью и отсечением композиции.
1.5. Строгие симметрии закона: автоморфизмы таблицы
Пусть задана система (Z_n, OP), где OP — либо PLUS, либо STAR.
Биекция
sigma: Z_n -> Z_n
называется строгой симметрией (автоморфизмом), если для всех x,y из Z_n выполняется
sigma( OP(x,y) ) = OP( sigma(x), sigma(y) ).
Для STAR-канона добавляется обязательная фиксация поглощающего элемента:
sigma(0) = 0.
Обозначу:
Aut(Z_n, OP) — группа автоморфизмов, S0(n) = |Aut(Z_n, OP)| — число строгих симметрий.
1.5.1. Формула для PLUS-канона
Для (Z_n, PLUS) автоморфизмы имеют вид:
sigma_u(x) = (u*x) mod n,
где gcd(u,n)=1.
Отсюда:
S0(n) = phi(n),
где phi(n) — функция Эйлера (количество u в {1,...,n-1}, взаимно простых с n).
Замечание о STAR. Для указанного STAR(SUN) в принятом каноне строгие симметрии согласованы с PLUS при условии sigma(0)=0; однако если STAR меняется (например, меняется правило на ненулевом слое), то S0(n) должно подтверждаться гейтами, а не «по аналогии».
1.6. Кадровые симметрии: аффинная группа Aff(n)
Строгая симметрия сохраняет закон в фиксированном кадре. Но в инженерном протоколе часто допустима смена кадра: «какая метка считается нулём», «где начало отсчёта», «какой сдвиг координат выбран».
Определяю кадровые преобразования:
f_{u,t}(x) = (u*x + t) mod n,
где gcd(u,n)=1, t in Z_n.
Множество всех таких преобразований образует группу Aff(n). Её мощность:
S1(n) = |Aff(n)| = n * phi(n).
Это второй счётчик уровня Ln: число допустимых перенастроек координат (кадра) при сохранении обратимости масштабирования и допустимости сдвига.
1.7. Два разных уровня эквивалентности: таблицы и конфигурации
Здесь принципиально важно развести две разные задачи, которые часто смешивают.
1.7.1. Лока таблиц (эквивалентность законов)
Есть множество операций OP на Z_n. Две операции OP и OP' считаются изоморфными, если существует биекция pi: Z_n -> Z_n такая, что
pi( OP(x,y) ) = OP'( pi(x), pi(y) ) для всех x,y.
Это эквивалентность самих законов (таблиц Кэли). Здесь живёт группа Aut(Z_n, OP) как автоморфизмы одного закона.
1.7.2. Лока конфигураций (орбиты при смене кадра)
Даже при фиксированном законе OP можно рассматривать конфигурации (пары, тройки, эпизоды) из Z_n и факторизовать их по действию кадровой группы Aff(n). Это уже не про «какой закон», а про «какие конфигурации неразличимы при допустимой смене координат».
То есть:
изоморфизмы таблиц = симметрии закона как алгебры,
орбиты конфигураций = симметрии представления/кадра, действующие на выбранные конфигурации.
Вся дальнейшая «орбитальная факторизация» относится ко второму уровню: к конфигурациям и действию Aff(n).
1.8. «Закон вихря» в минимальной инженерной форме
Теперь можно записать «вихрь» как последовательность вычислимых объектов:
фиксирую Ln: множество Z_n;
фиксирую канон операции OP (PLUS или STAR(SUN)) как таблицу Кэли;
вычисляю S0(n) = |Aut(Z_n, OP)| (строгие симметрии закона);
фиксирую кадровую группу Aff(n) и счётчик S1(n) = |Aff(n)|;
перехожу к факторизации конфигураций по Aff(n), получая орбиты и типы (это будет в Главе 2);
ввожу гейты, которые проверяют, что все эти величины действительно совпадают с каноном.
Смысл этой дисциплины: система различения объявляется «существующей» не потому, что она красиво описана, а потому что она проходит проверки, которые нельзя пройти риторикой.
1.9. Примеры счётчиков для L1–L5 (для ориентира)
Здесь я фиксирую базовые значения, которые затем должны подтверждаться валидаторами.
L1: n=1 phi(1)=1, tau(1)=1 (значения тривиальны, так как различения нет).
L2: n=2 phi(2)=1, поэтому S0(2)=1, S1(2)=2.
L3: n=3 phi(3)=2, поэтому S0(3)=2, S1(3)=6.
L4: n=4 phi(4)=2, поэтому S0(4)=2, S1(4)=8.
L5: n=5 phi(5)=4, поэтому S0(5)=4, S1(5)=20.
Факторизация пар (Q_pairs(n)) и строгая нормализация орбит — предмет Главы 2.
1.10. Итог главы 1
Уровень Ln задаётся конечным множеством Z_n и таблицей Кэли выбранного канона операции (PLUS или STAR(SUN)).
Строгие симметрии закона — автоморфизмы; в PLUS-каноне их число равно S0(n)=phi(n).
Кадровые симметрии задаются аффинной группой Aff(n); её мощность S1(n)=n*phi(n).
Разведены два типа эквивалентности: изоморфизмы таблиц (законов) и орбиты конфигураций при смене кадра.
«Закон вихря» фиксирован как протокол: таблица -> симметрии -> факторизация -> канон -> гейты.
Глава 2. Орбитальная факторизация конфигураций: пары и тройки под действием Aff(n)
В Главе 1 я развёл два уровня: (i) законы (таблицы Кэли и их изоморфизмы), (ii) конфигурации внутри фиксированного носителя и их факторизация по кадровым симметриям. Теперь я делаю следующий шаг закона вихря: формализую орбитальную факторизацию пар и затем троек при действии аффинной группы
Aff(n) = { f_{u,t}(x) = (u*x + t) mod n | gcd(u,n)=1, t in Z_n }.
Ключевой инженерный смысл: мы больше не рассматриваем «все пары/тройки как есть», а работаем с типами (орбитами), которые и являются устойчивыми объектами уровня.
2.1. Действие Aff(n) на конфигурациях
2.1.1. Упорядоченные пары
Множество упорядоченных пар:
OrdPair(n) = Z_n x Z_n.
Действие Aff(n):
f_{u,t} . (x,y) = (ux + t, uy + t) mod n.
2.1.2. Неупорядоченные пары
Множество неупорядоченных пар (мультимножества размера 2):
UnordPair(n) = { {x,y} | x,y in Z_n }.
Действие:
f_{u,t} . {x,y} = { f_{u,t}(x), f_{u,t}(y) }.
2.1.3. Упорядоченные тройки
Множество троек:
Triad(n) = Z_n x Z_n x Z_n,
действие:
f_{u,t} . (x,y,z) = (ux + t, uy + t, u*z + t) mod n.
2.2. Пары: нормализация и Лемма 1 (строго)
Я даю полную классификацию орбит упорядоченных пар и сразу получаю формулы числа орбит.
Определение (разность и gcd-инвариант)
Для пары (x,y) определим
Delta(x,y) = (y - x) mod n,
d(x,y) = gcd(Delta(x,y), n).
Лемма 1 (классификация орбит упорядоченных пар)
Лемма 1. Две упорядоченные пары (x,y) и (x',y') лежат в одной орбите действия Aff(n) тогда и только тогда, когда
gcd(y-x, n) = gcd(y'-x', n).
То есть орбиты OrdPair(n)/Aff(n) классифицируются делителями d | n.
Доказательство (через нормализацию пары)
Шаг 1. Инвариантность gcd. Пусть f_{u,t} in Aff(n). Тогда
Delta(f.(x,y)) = (uy + t) - (ux + t) = u*(y-x) mod n.
Следовательно,
gcd(Delta(f.(x,y)), n) = gcd(u*Delta(x,y), n) = gcd(Delta(x,y), n),
поскольку gcd(u,n)=1. Значит d(x,y) неизменен на орбите.
Шаг 2. Нормализация сдвигом: (x,y) -> (0,Delta). Возьмём f_{1,-x}. Тогда
f_{1,-x}.(x,y) = (0, y-x) = (0,Delta).
Значит каждая орбита содержит представителя вида (0,Delta).
Шаг 3. Сведение к действию единиц на Delta. Преобразование f_{u,0} даёт
f_{u,0}.(0,Delta) = (0, u*Delta).
Поэтому два представителя (0,Delta) и (0,Delta') лежат в одной орбите тогда и только тогда, когда существует u с gcd(u,n)=1 такое, что
Delta' = u*Delta mod n.
Шаг 4. Транзитивность на множествах с фиксированным d. Пусть d = gcd(Delta,n) = gcd(Delta',n). Тогда
Delta = da, Delta' = da',
где gcd(a, n/d)=gcd(a', n/d)=1.
В модуле m = n/d элементы a и a' обратимы, значит существует u0 такое, что
u0*a = a' mod m.
Тогда u0Delta = Delta' mod n. Выбирая представителя u congruent u0 mod m и взаимно простой с n (это реализуемо стандартной конструкцией по CRT), получаем требуемое u in Z_n^. Следовательно, все Delta с одним и тем же d лежат в одной орбите.
Итак, d полностью классифицирует орбиту. Лемма доказана. QED.
2.3. Число орбит пар: упорядоченные и неупорядоченные (разные объекты)
Теперь я фиксирую именно то, что вы требовали: формулы для числа орбит разных объектов, а не «всё одно и то же».
2.3.1. Упорядоченные пары (включая диагональ)
Из Леммы 1:
| OrdPair(n) / Aff(n) | = tau(n),
где tau(n) — число положительных делителей n.
Канонический представитель орбиты, соответствующей делителю d | n:
(0,d).
Диагональ (x=x) соответствует Delta=0, то есть d=n.
2.3.2. Упорядоченные пары без диагонали
Определим
OrdPair_neq(n) = { (x,y) in Z_n x Z_n | x не равно y }.
Это ровно исключение Delta=0, то есть исключение d=n. Следовательно,
| OrdPair_neq(n) / Aff(n) | = tau(n) - 1.
2.3.3. Неупорядоченные пары (включая диагональ)
Объект другой:
UnordPair(n) = { {x,y} | x,y in Z_n }.
Хотя объект другой, число орбит совпадает по причине того, что в Aff(n) есть преобразование, меняющее элементы местами.
Факт (swap лежит в Aff(n)). Для любой пары x,y преобразование
s_{x,y}(z) = (-1)*z + (x+y) mod n
меняет x и y местами:
s_{x,y}(x)=y, s_{x,y}(y)=x.
Значит порядок внутри пары не является дополнительным инвариантом: он уже факторизован действием группы.
Отсюда:
| UnordPair(n) / Aff(n) | = tau(n).
2.3.4. Неупорядоченные пары без диагонали
Определим
UnordPair_neq(n) = { {x,y} | x не равно y }.
И снова исключается только класс Delta=0, значит:
| UnordPair_neq(n) / Aff(n) | = tau(n) - 1.
2.3.5. Примеры (контроль здравого смысла)
n=4: tau(4)=3 Орбиты упорядоченных пар: d in {1,2,4}. Без диагонали: 2 орбиты (d=1 и d=2).
n=5: tau(5)=2 Орбиты: d in {1,5}. Без диагонали: 1 орбита (все разные пары эквивалентны).
Это и есть строгая причина, почему на уровне пар «L3 и L5 выглядят одинаково», а L4 даёт третий тип связи: это не «мистика триады», а арифметика делителей n.
2.4. Тройки: нормализация и триадный инвариант (невырожденный режим)
Теперь я перехожу от пар к тройкам. Именно здесь появляется первый содержательный слой «вихря» как отличия между уровнями: на парах всё держится на gcd, на тройках появляется параметр отношения.
2.4.1. Нормализация тройки аффинным действием
Для тройки (x,y,z) применим сдвиг t=-x:
(x,y,z) -> (0, y-x, z-x) = (0, a, b),
где
a = (y-x) mod n, b = (z-x) mod n.
Затем применим масштабирование u (gcd(u,n)=1):
(0,a,b) -> (0, ua, ub).
То есть классификация троек сводится к классификации пар (a,b) с одновременным умножением на единицу u.
2.4.2. Невырожденные тройки и инвариант r
Критически важна обратимость a. Если gcd(a,n)=1, то a обратим по модулю n, и можно нормализовать a в 1:
выбираем u = inv(a) mod n,
получаем:
(0, a, b) -> (0, 1, r),
где
r = b * inv(a) mod n.
Итак, в невырожденном режиме (gcd(a,n)=1) тройка классифицируется параметром r.
Это и есть ваш триадный инвариант:
Delta1 = (y-x) mod n Delta2 = (z-x) mod n если gcd(Delta1,n)=1, то r = Delta2 * inv(Delta1) mod n.
2.4.3. Инвариантность r при действии Aff(n) (в невырожденном режиме)
Пусть f_{u,t} действует на (x,y,z). После нормализации к (0,Delta1,Delta2) мы имеем:
Delta1 -> uDelta1, Delta2 -> uDelta2.
Тогда
r' = (uDelta2) * inv(uDelta1) mod n = (u*Delta2) * (inv(Delta1)*inv(u)) mod n = Delta2 * inv(Delta1) mod n = r,
поскольку u обратим. Значит r — инвариант орбиты (при условии gcd(Delta1,n)=1).
2.5. Вырожденные тройки: когда inv(Delta1) не существует
Если gcd(Delta1,n) не равно 1, то инвариант r в форме выше не определён. Тогда классификация троек требует дополнительной структуры: появляются классы, зависящие от делителя d = gcd(Delta1,n), и инвариант строится уже в модуле n/d.
Практически для инженерного протокола достаточно разделить тройки на три класса:
дегенерация по совпадению: y=x или z=x (Delta1=0 или Delta2=0);
полувырожденный режим: gcd(Delta1,n)=d>1, но Delta1 не равно 0;
невырожденный режим: gcd(Delta1,n)=1.
В законе вихря именно этот разрыв и существенен: на уровне L4 (n=4) возникает промежуточный делитель 2, который создаёт устойчивый «полувырожденный» слой троек, невозможный для простых n.
2.6. Итог главы 2
Действие Aff(n) на парах позволяет строго классифицировать орбиты через d=gcd(Delta,n).
Число орбит упорядоченных пар и неупорядоченных пар (как разных объектов) равно tau(n); без диагонали равно tau(n)-1.
На тройках действует строгая нормализация: (x,y,z) -> (0,Delta1,Delta2) -> (0,1,r) в невырожденном режиме gcd(Delta1,n)=1, где r=Delta2*inv(Delta1) mod n — инвариант орбиты.
Вырожденные режимы троек появляются там, где у n есть нетривиальные делители (в частности, n=4), и именно они дают новый слой различения, который не виден на парах.
Глава 3. Закон вихря как вычислимая дисциплина: две категории, гейты, канон и спираль уровней
В Главе 1 я задал уровень Ln как (Z_n, OP) и развёл симметрии закона (Aut) и кадровые преобразования (Aff). В Главе 2 я построил орбитальную факторизацию конфигураций (пары и тройки) под действием Aff(n) и дал строгие формулы числа орбит и нормализацию (Лемма 1). Теперь я делаю последний шаг: оформляю «закон вихря» как строгую вычислимую процедуру, фиксируя:
(i) явное категориальное различение «конфигураций» и «изоморфизмов таблиц»; (ii) канонический набор счётчиков уровня и их места в протоколе; (iii) систему гейтов/валидаторов как форму инженерной верификации; (iv) «спираль уровней» L1 -> L2 -> ... как повторяющийся цикл: симметрии -> орбиты -> канон -> переход.
Все формулы даны в ASCII.
3.1. Две разные категории: таблицы (законы) и конфигурации (наблюдаемые)
Ключевая строгость, без которой метод постоянно «плывёт»: нельзя смешивать
изоморфизмы таблиц (симметрии/переопределения закона), и
эквивалентность конфигураций (калибровочная смена кадра для наблюдаемых объектов).
Я фиксирую это как две категории.
3.1.1. Категория таблиц Кэли: CayleySys_n
Объекты. Объектом является пара (Z_n, OP), где OP: Z_n x Z_n -> Z_n — бинарная операция (закон), заданная таблицей Кэли.
Морфизмы. Морфизмом (изоморфизмом) между (Z_n, OP) и (Z_n, OP') является биекция
pi: Z_n -> Z_n
такая, что для всех x,y:
pi( OP(x,y) ) = OP'( pi(x), pi(y) ).
Композиция морфизмов — обычная композиция биекций. Тождественный морфизм — тождественная биекция.
Автоморфизмы. Aut(Z_n, OP) — группа автоморфизмов объекта (Z_n, OP) в этой категории.
Это и есть «строгие симметрии таблицы» в математическом смысле.
3.1.2. Категория конфигураций: Config_n
Здесь объектами служат не законы, а пространства конфигураций на фиксированном носителе Z_n, а морфизмы — кадровые преобразования.
Объекты. Для каждого типа конфигураций k я задаю объект:
Conf_k(n) = Z_n^k
(например, k=2 — пары, k=3 — тройки). При необходимости фиксируются подмножества (например, без диагонали).
Морфизмы. Морфизмом выступает преобразование из Aff(n), действующее диагонально:
f_{u,t}(x_1,...,x_k) = (ux_1 + t, ..., ux_k + t) mod n, где gcd(u,n)=1, t in Z_n.
Орбиты. Фактор-объект (на уровне множеств) определяется как множество орбит:
Conf_k(n) / Aff(n).
Эти орбиты — не «симметрии закона», а типы конфигураций при смене кадра.
3.1.3. Почему это различение принципиально
В CayleySys_n мы сравниваем законы: одна таблица Кэли может быть изоморфна другой.
В Config_n мы сравниваем представления одного и того же пространства: разные координаты и разные сдвиги считаются калибровочно эквивалентными.
Смешение этих уровней ведёт к логическим ошибкам: например, утверждать «таблица изменилась», когда на деле произошла только смена кадра, или наоборот, «это просто переименование», когда реально изменён закон OP.
3.2. Канонический набор счётчиков уровня Ln
В вашей дисциплине «уровень» считается фиксированным, только если проходит проверяемый набор инвариантов. В базовой версии (для PLUS-канона, а STAR(SUN) проверяется гейтами отдельно) это три счётчика:
(1) S0(n) = |Aut(Z_n, OP)| (строгие симметрии закона), (2) S1(n) = |Aff(n)| (кадровые симметрии), (3) Q_pairs(n) = |OrdPair(n)/Aff(n)| = tau(n) (типы связей на парах).
Из Главы 1 и 2:
S0(n) = phi(n) (для OP=PLUS), S1(n) = n*phi(n), Q_pairs(n) = tau(n).
Дополнительно (различение объектов, требуемое строгостью):
Q_pairs_neq(n) = |OrdPair_neq(n)/Aff(n)| = tau(n) - 1, и те же значения для неупорядоченных пар.
3.3. «Вихрь» как протокол: симметрии -> орбиты -> канон -> гейты
Теперь я фиксирую сам закон вихря в форме вычислимого цикла.
3.3.1. Определение (вихревой цикл уровня Ln)
Вихревой цикл уровня Ln — это алгоритм:
Step A (Law): зафиксировать закон OP (таблицу Кэли) на Z_n. Step B (Aut): вычислить Aut(Z_n, OP) и счётчик S0(n). Step C (Frame): зафиксировать Aff(n) и счётчик S1(n). Step D (Orbits): факторизовать конфигурации (пары/тройки/эпизоды) по Aff(n), получив Q-слои. Step E (Canon): выбрать канонических представителей орбит (нормализация). Step F (Gates): прогнать гейты, подтверждающие совпадение с каноном. Step G (Lift): определить переход Ln -> Lm (например, n -> n+1 или другие лифты), проверяя совместимость счётчиков/слоёв.
Смысл: «вихрь» не производит текст, а производит канонизированное состояние и протокол проверки.
3.4. Канонизация (нормализация) как обязательный элемент протокола
Без канонизации орбитальная факторизация остаётся «абстрактной». Канонизация делает её инженерно применимой: любой объект приводится к стандартной форме.
3.4.1. Канон пары
Для упорядоченной пары (x,y):
сдвигом t=-x приводим к (0,Delta),
далее классифицируем по d=gcd(Delta,n),
в каноне выбираем представителя (0,d).
Это и есть канонизация орбит пар.
3.4.2. Канон невырожденной тройки
Для тройки (x,y,z):
сдвигом t=-x приводим к (0,Delta1,Delta2),
если gcd(Delta1,n)=1, умножением u=inv(Delta1) приводим к (0,1,r), где r = Delta2*inv(Delta1) mod n.
Здесь (0,1,r) — канонический представитель орбиты в невырожденном классе.
Вырожденные классы требуют отдельного канона (по делителю d=gcd(Delta1,n)), и именно это является источником дополнительных слоёв различения для составных n.
3.5. Гейты и валидаторы: инженерная форма строгой проверяемости
Я фиксирую гейты как проверяемые контракты. Результат прогона валидаторов должен быть не «правдоподобный текст», а формальный исход:
Outcome in {PASS, BLOCK, REPAIR}, Trace: список применённых шагов/проверок, Repair: минимальное исправление (если применимо).
Ниже базовый набор гейтов, достаточный для строгого ядра статьи.
3.5.1. Гейты уровня закона (таблица Кэли)
G_LAW_1 (closure): для всех x,y в Z_n OP(x,y) в Z_n. G_LAW_2 (PLUS canonical): OP(x,y) = (x+y) mod n (если заявлен PLUS-канон). G_LAW_3 (STAR SUN): если заявлен STAR(SUN), то:
OP(0,x)=0 и OP(x,0)=0 для всех x,
OP(x,y)=(x+y) mod n для x не равно 0,y не равно 0.
Замечание: фразу «STAR не обязана быть ассоциативной» я оставляю только как потенциальную свободу модели. В текущем каноне STAR определён явно; вопрос ассоциативности решается вычислительно отдельным гейтом (если он нужен), а не утверждением в тексте.
3.5.2. Гейты строгих симметрий (Aut)
G_AUT_1 (homomorphism): sigma(OP(x,y)) = OP(sigma(x),sigma(y)) для всех x,y. G_AUT_2 (SUN fixed): для STAR sigma(0)=0. G_AUT_3 (count): |Aut(Z_n,OP)| = S0(n); для PLUS-канона S0(n) = phi(n).
3.5.3. Гейты кадровых симметрий (Aff)
G_AFF_1 (form): допускаются только f_{u,t}(x)=(ux+t) mod n, gcd(u,n)=1. G_AFF_2 (count): |Aff(n)| = nphi(n). G_AFF_3 (action): действие на конфигурациях должно быть диагональным и согласованным.
3.5.4. Гейты орбитальной факторизации конфигураций
G_ORB_PAIR_1 (pair invariant): d=gcd(y-x,n) инвариант при Aff(n). G_ORB_PAIR_2 (pair orbit count): |OrdPair(n)/Aff(n)| = tau(n). G_ORB_PAIR_3 (pair orbit count no diag): |OrdPair_neq(n)/Aff(n)| = tau(n)-1.
G_ORB_TRIAD_1 (triad normalization): (x,y,z) канонизируется к (0,Delta1,Delta2). G_ORB_TRIAD_2 (triad invariant): если gcd(Delta1,n)=1, то r=Delta2*inv(Delta1) mod n инвариант.
3.5.5. Что означает REPAIR в этой статье
В контексте данной статьи REPAIR — это минимальная правка спецификации, приводящая структуру к канону. Типичные ремонты:
исправить таблицу OP в клетках, где нарушен канон,
исправить роль SUN или условия STAR,
исправить допустимый класс кадровых преобразований (запретить u с gcd(u,n) не равно 1),
исправить процедуру канонизации (например, неверно взят инвариант).
REPAIR всегда должен быть формулирован как конечный атомарный патч, а не как «переписать теорию».
3.6. Спираль уровней: от L1 к Ln как повторяющаяся конструкция различения
Теперь я формулирую «многополярную спираль» строго, как итеративную процедуру.
3.6.1. L1 как нулевая точка различения
L1: n=1, Z_1={0}. Здесь:
закон OP тривиален (единственная таблица),
Aut имеет мощность 1,
Aff имеет мощность 1,
конфигурации не содержат различий (всё диагонально).
Инженерно: в L1 нет нетривиальных симметрий и нет пространства различения.
3.6.2. Переход Ln -> Lm как лифт с проверкой совместимости
Переход уровня — это не «прибавить ещё одну метку». Это:
определить отображение lift: Z_n -> Z_m (или более общий подъём конфигураций),
проверить, что lift совместим с выбранным каноном закона и кадровыми преобразованиями,
проверить согласование счётчиков и орбитальных слоёв (гейты вложенности).
Уровни образуют спираль, потому что каждый шаг обязательно включает цикл:
Law -> Symmetry -> Orbit -> Canon -> Gate -> Lift.
Это не линейное «описание мира», а дисциплина сборки: каждый виток переводит структуру в более богатое различение, но только при сохранении проверяемых инвариантов.
3.7. Итог главы 3 (финальная фиксация)
Я ввёл два строгих слоя как две категории: CayleySys_n: таблицы Кэли и их изоморфизмы (симметрии закона), Config_n: конфигурации и их факторизация по Aff(n) (симметрии кадра).
Я зафиксировал канонический набор счётчиков уровня Ln: S0(n)=phi(n) (для PLUS), S1(n)=n*phi(n), Q_pairs(n)=tau(n) и отдельно указал объекты без диагонали: tau(n)-1.
Я оформил «закон вихря» как вычислимый цикл: таблица -> Aut -> Aff -> орбиты -> канон -> гейты -> лифт.
Я зафиксировал гейты как инженерные контракты, дающие исходы PASS/BLOCK/REPAIR и трассу проверки.
Тем самым «многополярность» в этой постановке является не рассказом, а алгебраической системой различения, где утверждения сводятся к проверяемым инвариантам и орбитальной факторизации.
Заключение
В настоящей работе «закон вихря» был доведён до формы вычислимой дисциплины различения, в которой нет места метафорам: каждый тезис либо редуцируется к таблице Кэли и действию групп, либо блокируется гейтом как некорректный.
Главная методологическая фиксация состоит в строгом разведении двух уровней объектов.
Уровень законов (таблиц Кэли). Уровень Ln задаётся как система (Z_n, OP), где OP: Z_n x Z_n -> Z_n — бинарный закон, полностью определяемый таблицей Кэли. Изоморфизмы таких систем задаются биекциями pi: Z_n -> Z_n, сохраняющими закон: pi(OP(x,y)) = OP'(pi(x),pi(y)). Именно здесь определяются строгие симметрии закона (автоморфизмы) Aut(Z_n,OP) и счётчик S0(n). В PLUS-каноне получено каноническое значение: S0(n) = phi(n).
Уровень конфигураций (наблюдаемых объектов). Пары, тройки и более общие конфигурации рассматриваются как элементы Z_n^k и факторизуются не по изоморфизмам закона, а по кадровым преобразованиям, образующим аффинную группу: Aff(n) = { x -> (ux + t) mod n | gcd(u,n)=1, t in Z_n }. Её мощность фиксируется строго: S1(n) = |Aff(n)| = nphi(n). Орбитальная факторизация по Aff(n) переводит «сырые» конфигурации в типы (орбиты), которые и являются устойчивыми объектами уровня.
На этом основании построена орбитальная классификация пар, дающая первый универсальный инвариант различения. Для упорядоченной пары (x,y) введена разность Delta = (y-x) mod n и доказано, что орбиты действия Aff(n) на OrdPair(n)=Z_n x Z_n полностью классифицируются значением d = gcd(Delta,n). Отсюда получены явные формулы числа орбит: |OrdPair(n)/Aff(n)| = tau(n), |OrdPair_neq(n)/Aff(n)| = tau(n) - 1, и аналогичные значения для неупорядоченных пар (как отдельного объекта). Тем самым «типы связей» на парах фиксируются не интерпретацией, а арифметикой делителей n.
Для троек показано, что вихревой слой усложняется: после нормализации сдвигом (x,y,z)->(0,Delta1,Delta2) в невырожденном режиме gcd(Delta1,n)=1 возникает триадный инвариант r = Delta2 * inv(Delta1) mod n, который сохраняется при действии Aff(n). Это задаёт первый конструктивный механизм перехода от парных типов к триадным конфигурациям, где различение начинает зависеть не только от делителей, но и от отношения разностей.
Инженерная завершённость конструкции обеспечивается системой гейтов и валидаторов. Гейты фиксируют:
корректность закона (замкнутость и канон PLUS/STAR(SUN)),
корректность группы автоморфизмов и совпадение S0(n) с phi(n) (в PLUS-каноне),
корректность кадровой группы и совпадение S1(n) с n*phi(n),
корректность орбитальной факторизации (включая формулы для числа орбит на парах и нормализацию конфигураций). Выход процедуры принципиально имеет форму протокола: PASS/BLOCK/REPAIR, трасса проверок и (при необходимости) минимальный ремонт, а не риторическое «объяснение».
Тем самым закон вихря формулируется как повторяющийся вычислимый цикл: таблица Кэли -> симметрии закона Aut -> кадровые симметрии Aff -> орбиты конфигураций -> канон -> гейты -> переход уровня. В этой схеме «спираль уровней» L1->L2->... является не нарративом, а процедурой сборки: новый уровень допустим только тогда, когда он выдерживает проверяемую тройку счётчиков S0(n)=phi(n), S1(n)=n*phi(n), Q_pairs(n)=tau(n), и когда конфигурации приводятся к каноническим представителям орбит без скрытой подмены кадра.
Итоговая фиксация отличается простотой и жёсткостью. В данной постановке многополярность представляет собой алгебраическую систему различения, которая:
задаёт конечный алфавит состояний;
определяет закон композиции (в форме таблицы Кэли);
выявляет симметрии закона и симметрии кадра;
посредством орбитальной факторизации переводит конфигурации в устойчивые типы.
Любой спор о «правильности» в этой системе сводится к чисто вычислительным процедурам: необходимо проверить,
совпадают ли инварианты,
проходят ли конфигурации через заданные гейты,
корректна ли процедура канонизации.
Именно в этом ключе «закон вихря» формирует строгую структуру, которая:
не требует субъективной веры,
не зависит от интерпретаций,
опирается исключительно на формальные вычисления и проверяемые критерии.
Можно запустить проверки прямо в ChatGPT: создайте новый чат и прикрепите файл MP_YANTRA_CORE_iter127.zip первым сообщением и в том же сообщении отправьте ровно одну фразу:
Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива.
Далее ChatGPT распакует архив, запустит предусмотренный протокол и выполнит проверочные прогоны (bootstrap и валидаторы). В результате вы получите отчёты о прохождении гейтов, а также выводы по симметриям и их законам в виде файлов в папке REPORTS.
Уличная еда в Индии
Машинка для нарезки картофеля спиралью на Али, на Яндекс.Маркет
Реклама: ООО "АЛИБАБА.КОМ (РУ)" ИНН: 7703380158
От локальности границы к полям: буравчик в многополярной спирали L1–L4 и максвелловские тождества
Глава 1. Что я называю вихрем и почему это не «картинка с закрученными линиями»
1.1. Зачем мне вообще нужно слово «вихрь»
Я использую слово «вихрь» не как поэтический образ и не как красивую иллюстрацию. Я беру его потому, что оно на интуитивном уровне указывает на одну важную идею: есть правило обхода, и из этого правила неизбежно следуют строгие выводы.
Если говорить совсем просто, я рассматриваю вихрь как ответ на вопрос:
«Что получится, если я буду обходить вокруг чего-то по замкнутому пути и фиксировать, как меняется некоторое поле?»
Эта формулировка уже содержит главное: вихрь связан не с “красотой линий”, а с замкнутым обходом и с тем, что происходит при этом обходе.
1.2. Минимальная интуиция «на пальцах»
Я беру две ситуации, понятные школьнику.
Ситуация А: “нет вихря” Представьте склон горы. Если я иду по замкнутому кругу на одной высоте, я возвращаюсь в ту же точку и не обнаруживаю, что «накопил» какую-то разность высоты. Здесь изменение “в сумме” по кругу равно нулю.
Ситуация Б: “есть вихрь” Теперь представьте, что я иду по кругу вокруг водоворота или вокруг области, где “что-то закручено”. Я могу обнаружить устойчивый эффект обхода: например, направление силы или направление потока “ведёт” меня так, что по кругу возникает согласованная ориентация.
Главная мысль: вихрь — это про эффект обхода. Если эффект обхода существует, он должен быть описан не словами, а правилом: как именно устроен обход и что именно я измеряю.
1.3. Строгое определение: вихрь как оператор
Теперь я фиксирую строгий смысл.
Я считаю вихрь оператором, то есть правилом преобразования, которое действует на поле.
В самой сжатой форме я использую определение:
Γ_{pi_fix} := star_{pi_fix} o d
И сразу поясняю школьным языком, что здесь что означает (без усложнения):
d — это «правило границы/обхода»: оно переводит локальные данные в данные про обход. Грубо говоря, d отвечает на вопрос «что происходит, когда я беру границу у объекта» или «как выглядит изменение по контуру».
star_{pi_fix} — это «правило дуальности»: оно переводит описание «по границе» в описание «как это выглядит в соседнем типе величин» (например, от обхода по контуру к потоку через поверхность).
pi_fix — это фиксированная ветвь ориентации: я заранее объявляю, как я считаю направление обхода и как задаю ориентацию. Это не “вкус автора”, а часть строгого протокола.
Следовательно, вихрь у меня — это не рисунок и не метафора, а строго определённая композиция двух операций.
1.4. Почему я фиксирую ветвь pi_fix и знак m_sign
В школьных учебниках часто говорят: «используйте правило правой руки» — и на этом заканчивают обсуждение. В результате знак в формулах выглядит как соглашение.
Я делаю иначе. Я считаю, что любая фундаментальная теория должна явно фиксировать, что происходит при смене ориентации.
Я ввожу правило:
rev(pi_fix) ⇒ m_sign := −m_sign
То есть: если я переворачиваю ветвь ориентации (условно “читаю янтру наоборот” или “меняю направление обхода”), то знак меняется строго предсказуемо. Именно так я запрещаю скрытые соглашения вида «мы просто договорились о знаке».
Это важно, потому что вихрь — это объект, который чувствителен к ориентации. Если ориентация не фиксирована, любая формула типа curl/rot будет иметь скрытую неоднозначность.
1.5. Что вихрь “делает” в моей системе: три вопроса и три ответа
Чтобы определение не оставалось пустым символом, я обязуюсь отвечать на три вопроса.
Вопрос 1. Что именно делает вихрь? Он превращает «локальные данные» в «данные о закрутке/обходе». То есть он показывает, есть ли у поля ненулевая “циркуляция” вокруг малой области.
Вопрос 2. От чего он зависит? Он зависит:
от локальности (нужно, чтобы было определено “рядом” и “граница”),
от выбора ветви ориентации pi_fix,
от дуальности star_{pi_fix}, которая задаёт корректный переход между типами величин.
Вопрос 3. Какие инварианты он сохраняет? Он сохраняет строгую структурную дисциплину: если дважды брать границу, получается ноль:
d o d = 0
Это правило не является физическим предположением. Это логика границы: «у границы границы нет». Из этого далее возникают строгие тождества, которые в электродинамике превращаются в половину уравнений Максвелла.
1.6. Промежуточный итог главы 1
В рамках моей логики:
Вихрь — это не метафора и не рисунок, а оператор.
Я определяю его как Γ_{pi_fix} := star_{pi_fix} o d.
Я фиксирую ориентацию как обязательную часть протокола, а смену ориентации связываю со знаком по правилу rev(pi_fix) ⇒ m_sign := −m_sign.
Я считаю, что именно эта строгость превращает «вихрь» из слова в математический объект, из которого можно выводить дальнейшие законы.
Глава 2. Почему вихрь неизбежно требует локальности, и откуда берётся закон d o d = 0
2.1. Что я называю «локальностью» и почему без неё вихрь невозможен
Я фиксирую простое правило: вихрь имеет смысл только тогда, когда я могу говорить о “малой окрестности” и о “границе” этой окрестности.
Если я не могу отделить «внутри» от «снаружи», то я не могу задать:
замкнутый обход,
контур,
границу,
а значит — и саму идею «закрутки».
Поэтому локальность для меня — не философия и не выбор удобной геометрии, а логическая цена употребления слова «вихрь».
Именно здесь появляется минимальный носитель, на котором можно формально определить «обход»:
либо дискретный (граф/клеточный комплекс),
либо непрерывный (гладкие формы).
Я сознательно подчёркиваю: мне не нужно заранее “пространство как 3D”. Мне достаточно минимальной структуры “рядом/граница/обход”.
2.2. Минимальная модель локальности: «клетки» и оператор границы
Я объясняю так, чтобы было понятно школьнику.
Представим, что мир разбит на маленькие элементы:
точки (узлы),
отрезки между точками (рёбра),
маленькие “плитки” (грани),
и, если нужно, маленькие “объёмы”.
Это похоже на конструктор или мозаику. В математике это называется клеточный комплекс.
Теперь я ввожу оператор d — оператор границы/обхода:
он берёт, например, грань (“плитку”) и возвращает её границу (контур из рёбер),
берёт ребро и возвращает его границу (две вершины с ориентацией),
и так далее.
Самое важное здесь — не детали, а один структурный закон.
2.3. Центральный закон: «граница границы равна нулю»
Я фиксирую аксиому:
d o d = 0
Школьный смысл:
Если я беру границу у поверхности, получаю контур.
Если я беру границу у контура, я не получаю “границу границы” — потому что контур уже замкнут.
Пример на пальцах:
у квадрата граница — четыре стороны;
у этих четырёх сторон нет “края” как у незамкнутой линии: они уже замкнулись.
Это не физика, не модель и не гипотеза. Это логика понятия “граница”.
И теперь я делаю ключевой вывод: как только я ввёл вихрь как оператор, построенный через d, я автоматически попадаю в мир, где действует d o d = 0.
2.4. Почему из d o d = 0 появляется «первая половина законов поля»
В моей линии вихрь определяется как:
Γ_{pi_fix} := star_{pi_fix} o d
То есть вихрь использует d. Но d подчиняется d o d = 0. Отсюда неизбежно возникают тождества “типа Бьянки”.
Чтобы не перегружать формулами, я формулирую школьный смысл:
Если поле устроено так, что его можно описывать как “обход” (то есть оно согласовано с границами),
то при повторном применении “обхода обхода” я не получаю нового эффекта: он должен быть нулевой.
В строгих записях это выражается в форме тождества, которое в электродинамике становится гомогенной частью уравнений Максвелла (в корневой форме — через dF = 0).
Я специально подчёркиваю: в этой точке я ничего “не подгоняю”. Я получаю структуру автоматически, потому что:
вихрь требует границы,
граница требует d,
d требует d o d = 0.
2.5. Где здесь появляется дуальность star_{pi_fix} и почему она обязательна
Если у меня есть только d, у меня есть “обход”, но у меня ещё нет того, что в физике интерпретируется как “поток через поверхность” и т. п.
Здесь нужен второй кирпич — дуальность star_{pi_fix}:
она связывает описание “по границе” и описание “через внутренность”,
переводит между двумя типами величин (в нашей терминологии это удобно связывать с M/R-секторами и оператором Dual).
Я опять объясняю просто:
d говорит “что происходит по контуру”,
star позволяет говорить “что соответствует этому через поверхность” (и наоборот).
Без star вихрь остаётся “обходом по линиям”, но не превращается в объект, который связывает разные типы описаний поля.
2.6. Зачем я держу дисциплину ветви pi_fix: чтобы знак не был “по вкусу”
В школьных формулах знак часто прячут за «правило правой руки». Это удобный приём, но в теоретическом выводе он опасен: знак начинает выглядеть внешним соглашением.
Я запрещаю эту слабость. Я фиксирую:
есть ветвь pi_fix (как именно ориентирован обход/чтение),
есть инволюция rev(pi_fix),
есть закон знака:
rev(pi_fix) => m_sign := -m_sign
И я требую, чтобы дуальность и вихрь были согласованы с этим законом. Тогда:
смена ориентации меняет знак строго по протоколу,
а не потому, что “так принято”.
2.7. Промежуточный итог главы 2
Я получил жёсткую цепочку неизбежностей:
Я хочу определить вихрь строго ⇒ мне нужна локальность (иначе нет границы и обхода).
Локальность ⇒ я ввожу оператор границы d.
Понятие границы ⇒ автоматически действует закон d o d = 0.
Чтобы вихрь был не просто “обходом”, а полноценным оператором поля ⇒ я ввожу дуальность star_{pi_fix} и держу дисциплину ветви pi_fix и знака m_sign.
Именно эта цепочка подготавливает следующий шаг: я покажу, как из этих структур возникают канонические уравнения поля в корневом виде и почему переход к привычным школьным формулам (div/curl) является не “определением по учебнику”, а проекцией на измеримый уровень.
Глава 3. Как из вихря получается форма уравнений Максвелла и почему это выглядит как «четыре закона»
3.1. Что я считаю целью вывода
Цель: показать, что четыре известные школьные формулы Максвелла — это не «четыре отдельные идеи», а распаковка двух корневых структурных равенств, которые возникают из определения вихря и локальности.
Я работаю в логике уровней:
L2 — измеряемый слой: то, что дают приборы и школьные формулы (E, B, заряды, токи).
L3 — слой замыкания/согласования: правила, которые делают наблюдение воспроизводимым (включая то, что является «источником», а что — «вихрем/обходом»).
L4 — слой строгой ориентационной дисциплины: ветвь pi_fix, инволюция rev(pi_fix) и закон знака m_sign, плюс дуальность между секторами.
Ключевой принцип: я не вставляю уравнения Максвелла как постулат. Я фиксирую структуру вихря и локальности и затем показываю, что из этого неизбежно получается знакомая школьная форма.
3.2. Две корневые формулы, из которых «вырастают» четыре уравнения
Я использую минимальную каноническую запись, где поле описывается двумя объектами и источником:
F — «полевой объект» (в классической математике это удобно понимать как 2-форму; школьнику достаточно: это объект, который умеет давать поток и обход).
G — «дуальный полевой объект» (получается из F через дуальность: G := star_{pi_fix}(F) или через оператор Dual между секторами M/R).
J — источник (заряд и ток в одном объекте).
Тогда канон записывается так:
dF = 0
dG = J
Это и есть две «половины» Максвелла в корневом виде.
Важно: здесь я сразу обозначаю, что из них следует то, что школьники знают как «четыре уравнения». Почему четыре? Потому что при переходе к измеримому описанию (L2) эти две формулы распадаются на компоненты.
3.3. Почему dF = 0 является структурной неизбежностью
Я не делаю вид, будто это магия. Я фиксирую логическую причину.
Если у меня есть оператор границы/обхода d и он удовлетворяет:
d o d = 0
то любая согласованная конструкция «вихревого» типа обладает тождествами, где повторный “обход” даёт ноль. Это и есть смысл dF = 0: поле F устроено так, что оно согласовано с локальностью, и «граница границы» не производит новых эффектов.
Школьный перевод: «Если я обхожу границу, то у этого обхода нет “края”, поэтому в замкнутой структуре возникают нулевые тождества.»
3.4. Почему dG = J — минимальная и единственная допустимая форма источников
Теперь я объясняю вторую половину так, чтобы было ясно.
Если в мире существуют заряды и токи, то они проявляются как источники поля. В корневой структуре “источник” — это ровно то, что стоит в правой части уравнения для дуального поля:
dG = J
Это минимальный постулат содержательной части: «источник действительно является источником для дуального поля». Он не подменяет вывод, потому что:
он вводит источники как единственный допустимый разрыв симметрии, не разрушая локальность;
из него автоматически следует закон сохранения.
3.5. Почему закон сохранения получается автоматически
Это место принципиально важно, и я формулирую его максимально жёстко.
Если:
dG = J
то применяю d к обеим сторонам:
d(dG) = dJ
левая часть равна нулю, потому что d o d = 0. Значит:
dJ = 0
Школьный перевод: «Если источник возникает как граница чего-то, то он не может появляться и исчезать произвольно. Он обязан сохраняться.»
В классическом языке это превращается в уравнение непрерывности: сохранение заряда.
3.6. Где именно появляются привычные «div» и «curl»
Школьник привык к словам:
div (дивергенция),
curl (ротор, вихрь).
Я подчёркиваю: в моей логике это не первичные символы, а сокращения для композиций через d и star_{pi_fix}.
Я фиксирую:
curl_{pi_fix} := star_{pi_fix} o d (это и есть мой вихрь Γ)
div_{pi_fix} := star_{pi_fix} o d o star_{pi_fix} (в нужных рангах)
То есть школьные операции «div» и «curl» я рассматриваю как «удобные имена» для строгих операторов, которые:
зависят от ветви pi_fix,
меняют знак строго по rev(pi_fix) => m_sign,
и поэтому не содержат скрытых соглашений.
3.7. Почему получается именно четыре школьных уравнения
Теперь я объясняю это просто, но строго.
Корневых формул две: dF = 0 и dG = J.
Когда я перехожу к измеримому описанию (L2), я раскладываю эти объекты на компоненты, которые школьнику известны:
из F получаются E и B,
из G получаются D и H,
из J получаются ρ (заряд) и J_vec (ток).
Тогда каждая корневая формула даёт два уравнения: одно «про дивергенцию», другое «про вихрь и время». Поэтому всего четыре.
В привычной записи это выглядит так:
Из dF = 0:
div B = 0
curl E + dB/dt = 0
Из dG = J: 3) div D = ρ 4) curl H - dD/dt = J_vec
Понятный смысл:
две формулы говорят про «замкнутость» поля и отсутствие произвольных “краёв” у вихревых структур;
две формулы говорят про то, что источники (заряды и токи) — это единственно допустимый способ сделать поле неоднородным, и при этом источники обязаны сохраняться.
3.8. Почему это не «подгонка», а строгая конструкция
Я фиксирую отличия от типичного изложения.
В учебнике curl и div обычно вводят как определения на 3D-координатах и потом подбирают знаки «правой рукой».
Я делаю наоборот: сначала фиксирую локальность (d и d o d = 0), затем фиксирую дуальность и ориентационную ветвь (star_{pi_fix}, pi_fix, rev(pi_fix), m_sign), затем определяю вихрь как оператор (Gamma_{pi_fix}), и только после этого получаю привычные школьные уравнения как проекцию.
Следовательно, учебниковая форма здесь — не первоисточник, а следствие.
3.9. Итог всей статьи в одной жёсткой схеме
Я подвожу итог максимально компактно:
Я определяю вихрь строго: Gamma_{pi_fix} := star_{pi_fix} o d.
Я фиксирую логическую локальность, поэтому действует d o d = 0.
Тогда получаются две корневые формулы поля: dF = 0 и dG = J.
Из второй формулы автоматически следует сохранение источника: dJ = 0.
При распаковке на измеримый уровень (L2) эти две формулы дают четыре школьных уравнения Максвелла.
Глава 4. Почему это именно многополярная спираль и откуда берётся «вихревое» развитие L1→L4
Я называю эту конструкцию многополярной спиралью не как метафору, а как минимальную форму саморазвивающейся аксиоматики, где каждый следующий уровень (лока) возникает как вынужденное замыкание противоречий и недоопределённостей предыдущего.
1) L1: однополярность как «единство без различения»
L1 — это чистое «есть» (единство), которое само по себе не имеет внутреннего различения. У него нет «второго», чтобы измерить разность. Поэтому на L1 нельзя строго определить ни знак, ни направление, ни “что такое ноль/единица” как различимые объекты: это скорее пред-объект, “единый факт присутствия”.
Ключевой тезис: L1 не допускает операционального определения, потому что определение всегда требует различения (сравнения).
2) L2: появление различения как минимальный акт
Чтобы вообще начать что-то определять, я вынужден ввести минимальную различимость: «это» и «не-это», «плюс/минус», «есть/нет». Это и есть L2: базис измерения, где появляется разность и, следовательно, появляется возможность:
фиксировать наблюдаемое как значение,
говорить о противоположностях,
иметь простейшую “геометрию различения”.
Но L2 ещё не умеет замыкать процесс: он умеет различать, но не умеет гарантировать тождество через преобразования (например, при обходе, при смене точки зрения, при времени).
3) L3: замыкание как протокол тождества
L3 возникает как вынужденный шаг, когда я требую не просто различения, а воспроизводимости: «я сделал действие → получил изменение → сопоставил → восстановил тождество объекта/границы».
Это и есть то, что я называю замыканием: на L3 появляется цикл как смысловая единица (контур, повтор, возврат). Без L3 невозможно корректно определить “вихрь” даже интуитивно, потому что вихрь — это не точка и не отрезок, а обход, то есть структура, которая имеет смысл только в замкнутом протоколе.
4) L4: ветвление ориентации и строгий контроль знака
Когда я хочу сделать вихрь строгим, мне нужно решить главную проблему классической традиции: знаки и ориентации не должны зависеть от скрытых соглашений.
Это и есть L4: четырёхполярность как минимальная онтология, где:
есть фиксированная ветвь pi_fix,
есть инволюция rev(pi_fix),
и есть закон: rev(pi_fix) => m_sign := -m_sign.
Именно здесь вихрь превращается в строгий оператор: Gamma_{pi_fix} := star_{pi_fix} o d, где дуальность star_{pi_fix} обязана менять знак при смене ветви.
Откуда берётся спираль
Спираль возникает как неизбежная форма наращивания структуры, когда каждый новый уровень не отменяет предыдущий, а закрывает его недоопределённость, добавляя ровно одну критическую степень:
L1: единство без различения (нет критериев определения).
L2: различение (появляется измеримость).
L3: замыкание (появляется цикл и тождество через действие/обход).
L4: ориентационная дисциплина (появляется строгий контроль знаков и ветвления).
Почему это именно «спираль», а не «линейная лестница»? Потому что развитие идёт через повторяющийся мотив: каждый уровень порождает преобразования, которые требуют:
выделить локальную операцию (различение/обход),
замкнуть её (цикл, d o d = 0 как логическая цена границы),
согласовать знаки/ориентации (ветвь и инволюция),
снова породить более богатую структуру на следующем шаге.
То есть уровни развиваются не добавлением “новых объектов”, а закручиванием одного и того же протокола на более строгом уровне: различение → замыкание → ориентация → снова различение уже внутри более богатой симметрийной структуры.
Где в этой логике «ось спирали»
Ось спирали — это не геометрическая ось в 3D, а инвариантная линия протокола: то, что сохраняется при переходах L1→L2→L3→L4.
В минимальной формулировке ось — это требование:
локальность (операции должны быть локальными),
замыкание без произвола (d o d = 0 как неизбежность границы),
ветвевой контроль знака (rev(pi_fix) => m_sign),
запрет скрытого join (тождество должно быть либо выведено, либо явно маркировано).
Эта ось и делает эволюцию «спиральной»: я возвращаюсь к тем же операциям (различение, обход, дуальность), но на каждом витке они становятся строже и богаче.
Как ЗАПУСТИТЬ архив в новом чате ChatGPT
Вставьте архив и инструкции в первое сообщение нового чата.
Задавайте любые вопросы по теме статьи.