Математика простыми словами
1 пост

1 пост
К посту про то, что ребёнок подарил другому обувь. Вот оригинал:
1. Коты клевые
2. Размер 49.5 - это миф. Или я ещё не созрел
3. В стране очень много неустроенных баянистов
4. Наличие минусов - это плюс
5. Свежее - не значит хорошее
6. После репортажей паренька с фермы понимаешь дядю Федора
7. Чистомен не одинок
8. Пост о кулинарии может привести к срачу о политике
9. Ждать старости легче, когда знаешь, что у тебя есть сохраненное
10. Это одна из лучших волн постов
В последнее время часто постят информацию о том, что до Тарасов что-то начало доходить.
Обращаюсь к таким. Сделайте ещё одно усилие и представьте себе, что у вас там арийцев нет. А бандера - тварь и дегенерат. И героем он может быть только у мразей.
По мотивам Залипательная тригонометрия
В комментариях многие говорили, что всё равно не понимают, что такое синус, косинус, тангенс. Что вещи так и остались неясными. Постараюсь пролить свет, чтобы не было страха перед ними и было понятно, зачем они нужны.
Давай для начала поговорим об углах.
Представь обычную дверь. Если ты её приоткроешь и посмотришь вниз, то увидишь две линии – линия порога и линия двери. И они практически пересекаются.
И ты даже можешь представить, что чем сильнее ты ее открываешь, тем больше линии начинают расходиться. И наоборот, когда дверь закрываешь, то “расстояние” между линиями уменьшается и они практически начинают совпадать. Так вот, такое “расстояние” между линиями и называется углом.
Теперь пойдем дальше. Про треугольники, я уверен, тебе даже объяснять не надо. Ты знаешь, что треугольник – состоит из трех линий, которые образуют три угла. Т.е. между каждыми двумя линиями есть какое-то “расстояние”. Есть особые треугольники, у которых один из углов прямой, т.е. одна линия стоит строго поперек другой. Такие треугольники называются прямоугольными:
Стороны, которые образуют прямой угол – катеты, а другая сторона – гипотенуза.
Так вот, древние математики изучали геометрию как раз начиная с треугольников, линий и углов. Особенно они любили прямоугольные треугольники. Они много что-то там считали, выводили всякие формулы, доказывали и т.д. Главное, что когда они всё это делали, то стали замечать, что очень часто приходится делить один катет на гипотенузу, потом другой катет, потом катет на катет.
Подумали, посчитали и поняли одну вещь. Что если взять прямоугольный треугольник, отметить на нем линии, которые соединяют один катет и гипотенузу также под прямым углом, то деление этой линии на гипотенузу всегда будет одним и тем же числом. Класс.
А что у таких треугольников еще одинаковое? Правильно, углы. Вот и сказали, что мол давайте вот такие деления между катетами и гипотенузой как-то обозначим. Давайте, пусть, например, синус такого угла – это деление одного катета на гипотенузу. А какого катета, их же два? Ну, пусть того, который напротив этого угла. А косинус – это тогда деление другого катета на гипотенузу, т.е. прилежащего. Как запомнить и не путаться?
сИнус – прОтиволежащий
кОсинус – прИлежащий
Тангенс – это еще проще, деление противолежащего катета на прилежащий или:
Т.е. все эти функции нужны для представления отношений между катетами и гипотенузой. И запись вида sin(x) = y стоит воспринимать как "при таком угле будет такое деление противоположного катета на гипотенузу".
Конечно, дальше их будут использовать еще круче даже в таких областях, в которых, казалось бы, даже и треугольников-то нет. Но этого не хочу касаться сейчас, т.к. цель всё-таки дать представление, что этой вещи бояться не стоит.
На этих базовых вещах можно уже идти дальше. Математика прекрасна.
PS. Думаю, что стоит заранее написать, что, к сожалению, синус не поможет водить машину, готовить еду и познакомиться с девушкой. Про прикладные задачи, где его можно применять и почему тогда такую "бесполезную" вещь дают в школе, я расскажу отдельно.
Совет учащимся математике с трудностями по тригонометрии.
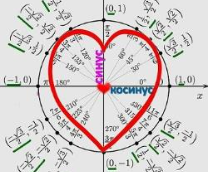
Сам я закончил матфак. Иногда смотрю материалы по математике, чтобы быть в тонусе и вот наткнулся на одно видео с визуализацией тригонометрических функций. И увидел такую картинку:
Я её никогда не видел и в таком виде тригонометрические функции не воспринимал. А теперь понял, что если бы мне её показали еще в школе, то со многими вещами было бы понятнее и не надо было бы ряд вещей зубрить.
Например, просто зная теорему Пифагора, можно легко вывести:
Надеюсь, пригодится в учебе. Еще раз убеждаюсь, что математика прекрасна.
Полное видео: