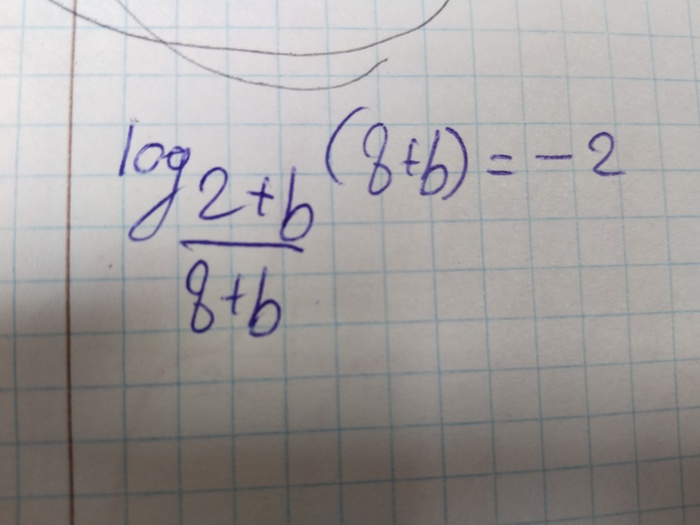В школе мы проходим много разных функций, а как они используются на практике мало кто запоминает, да и редко этому (самому важному!) вопросу на уроках уделяется должное внимание.

Что же, пожалуй мы сделаем целую серию статей по этому вопросу и будем периодически рассказывать о разных функциях, которые вам наверняка знакомы, но смысл их мало понятен. Это также полезно знать, как и разбираться, например, в способе проверки решения задачек размерностью. Тут я расписывал смысл этой методики, которая кажется мутной на первый взгляд.

Начнем с рогарифмов. Почему рогарифмы? Просто когда нам в школе о них впервые рассказывали, то ли преподаватель плохо букву выговаривал, то ли троллил нас, но весь класс на первом занятии записал именно "рогарифмы". Ну а мы-то конечно поговорим сейчас именно о логарифмах.

Что такое логарифм?

Википедия даёт такое определение:

Логарифм числа определяется как показатель степени, в которую надо возвести основание, чтобы получить число.

В общем-то, всё звучит очень просто. В какую степень возвести число, чтобы получить основание?

Все сложные математические действия и преобразования нас сейчас мало интересуют. Ведь мы ищем физический смысл этого понятия. Ну а в физике и в реальной жизни это не просто логарифм, а целая логарифмическая функция. Она мало отличается от приведенного примера, просто перед ним добавляют "ыгрик" = логарифм такой-то.

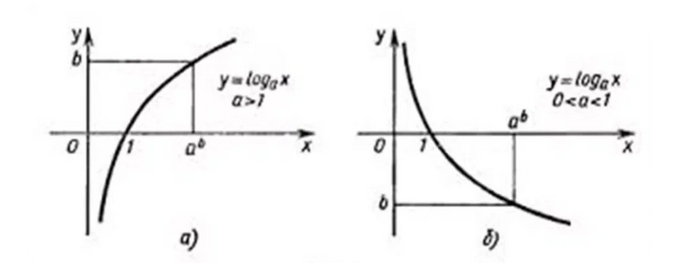
Эта функция описывает своеобразный график. Графиком функции является удобное изображение последовательности точек, которое показывает поведение функции при возрастании изменяемого параметра. Традиционно в функции есть "Ыкс" и "Ыгрик". Каждому икс будет соответствовать некоторое значение игрек. Когда обозначается последовательность таких точек и соединяется линией, выходит график и отображение зависимости. В случае логарифмической функции график такой:

Как применить логарифм в жизни

Известно, что каждый процесс в природе, как это ни странно, подчиняется некоторой закономерности. Закономерность и есть основа появления графика. График - это изображение закономерности. Самый простой вариант - линейная зависимость. Сюда подходят понятные и простые процессы.

Скажем, человек идёт с постоянной скоростью и нам надо графически изобразить, как он удаляется от дома с течением времени. Всё просто и линейно. За час он прошел 5 км. За два часа - 10 км и так далее. Рисуем прямую и всё. Таким образом можно хотя бы косвенно предположить, что график и дальше останется прямой и изменения будут линейными. Но это излишнее упрощение. В данном случае, человек устанет и пойдет со скоростью 3 км/ч.

Есть более сложные процессы, типа распространения волны. Там поиск той же координаты упирается в функцию синус и отображается синусоидой.

А что тогда показывает логарифм?

Удивительно, но такие процессы тоже есть!

Логарифмическая функция есть во всех областях человеческого знания. Даже в химии или биологии, а не только в физике. Логарифмические зависимости используются, например, если хочется узнать сколько сможет прожить кузов вашего автомобиля до полного ржавления.

Поэтому, перечислить абсолютно все примеры использования логарифма в физике и технике будет проблематично. Мы перечислим несколько примеров, а вы между тем запомните, что логарифм - это никакое не волшебное слово. Это просто очередная закономерность, под которую прекрасно подходят некоторые процессы в природе. И если координата точки при волновом процессе описывается синусоидой, то, например, интенсивность звука описывается логарифмической функцией. Кстати говоря, изучать различные эффекты по картинкам довольно просто и даже занятно. Я собираю коллекцию таких полезных картинок на отдельном телеграмм канале и приглашаю вас их посмотреть.

Конкретные примеры использования

Ну а теперь рассмотрим несколько конкретных примеров использования. Примечательно, что в физике логарифмическая функции применяется очень широко, но как правило не как самостоятельное описание процесса, а как часть, которая входит в состав сложных уравнений, описывающих физический процесс.

В физике оно часто обретает название экспонента. Не стоит его бояться :) Ведь это просто тоже самое, но с основанием е = 2,7.

Интенсивность звука в физике

Интенсивность звука или сила звука - это физическая величина, характеризующая мощность, переносимую звуковой волной в направлении распространения.

Согласитесь, показатель очень важный. Например, для того, чтобы организовать хорошую звукоизоляцию, нужно уметь посчитать сколько именно энергии принесет звуковая волна и насколько мощная нужна стенка.

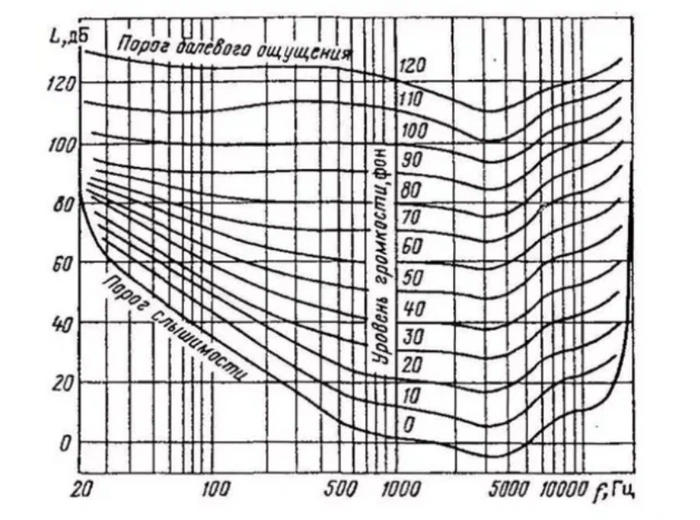
Для сравнения уровней интенсивности используется логарифмическая шкала. Почему логарифмическая? Потому что параметр зависит ещё и от частоты, а линейной закономерности тут нет. Изучите график и поймёте, в чем смысл. Разные частоты ведут себя по-разному и это не линейно. Так определяют, например, коэффициент звукоизоляции стен.

Распад радиоактивного вещества

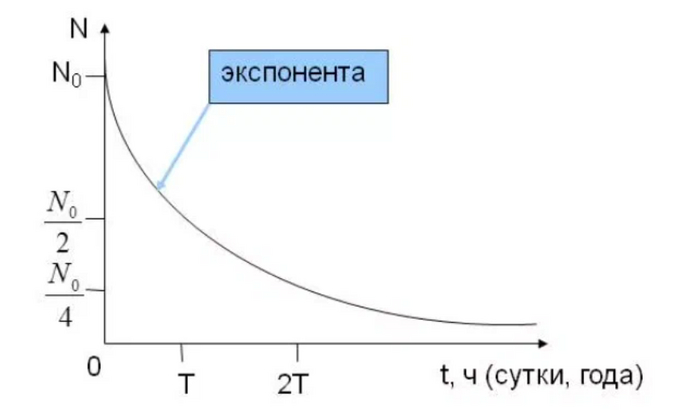
Число нераспавшихся ядер с течением времени описывается экспонентой.

По факту получается, что именно логарифмическая функция тут подошла под описание процесса радиоактивного распада. Всё логично - прошло больше времени и большее количество ядер распалось. Чем дольше ждем, тем больше ядер разваливается. Ну а для каждого вещества такая картинка будет своя. Вот только закономерность этого процесса примерно схожая.

Барометрическая формула

Наш друг Больцман постарался и вывел закономерность, по которой можно увидеть, как с высотой подъема над поверхностью земли убывает давление газа. Все ведь помнят, что в горах давление ниже, чем на равнине? Потому и вода кипит при более низких температурах и обделаться от плохо обработанной воды неправильно обработать питьевую воду можно не зная этой особенности.

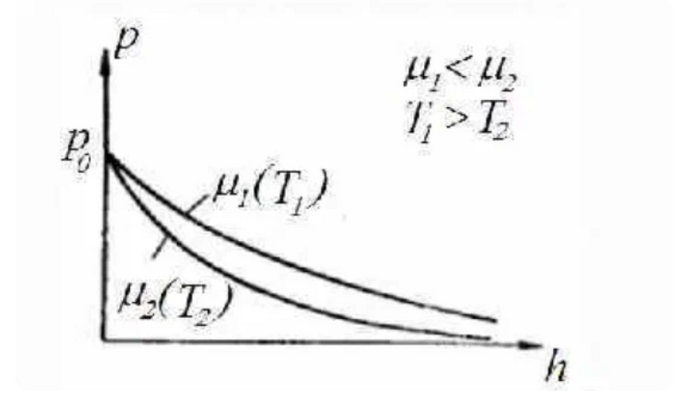
Барометрическая формула показывает, что с высотой давление спадает согласно логарифмической функции и тем быстрее, чем больше молярная масса газа или низкая температура.

Формула Циолковского

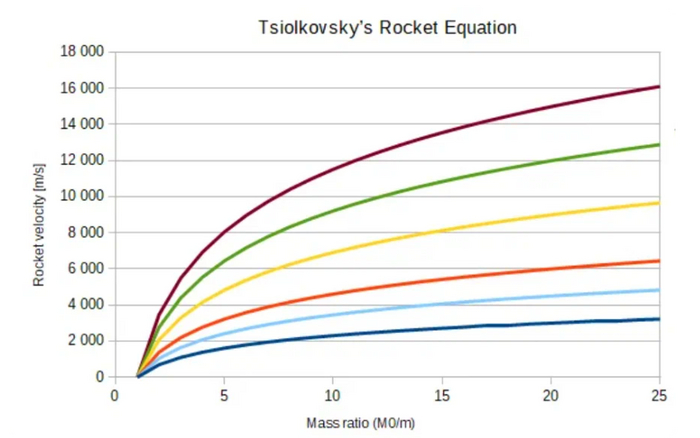
Чем больше конечная масса ракеты, тем больше должна быть и стартовая, а чем больше скорость истечения газов, тем больше может быть конечная масса ракеты.

Это закономерность, которая называется формулой Циолковского. Она описывает скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя в условии отсутствия всех других сил. Это один из значимых законов, которые важны для космической отрасли и, представьте себе, там логарифмическая функция.

Звёздная величина

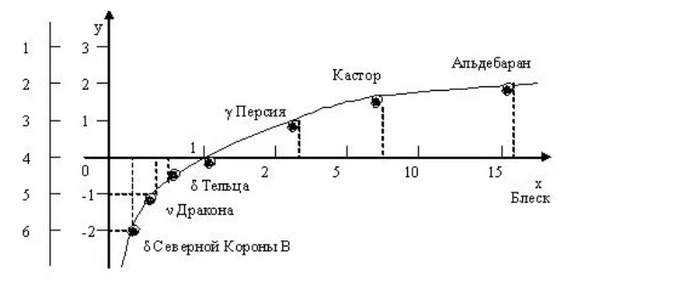
Звёздная величина или блеск звёзд - это безразмерная числовая характеристика яркости объекта.

Этот показатель довольно широко применяется в астрономии и позволяет описать яркость объекта в сравнении друг с другом.

Логарифмическая спираль

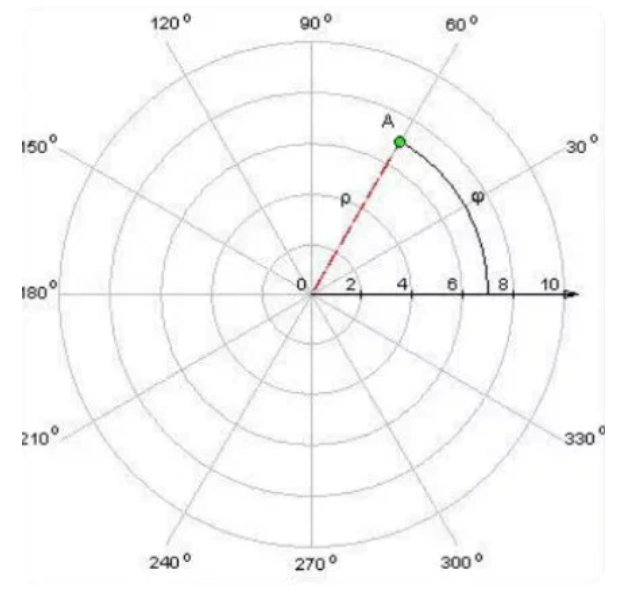
Было бы странным не упомянуть тут так называемую логарифмическую спираль. Теперь сделаем пакость и построим логарифмическую функцию в полярных координатах. Полярные координаты - это такие, где каждая точка описывается полярным углом и полярным радиусом. Говоря ещё более понятным языком - это круг, где есть величина, отложенная по оси, и угол поворота.

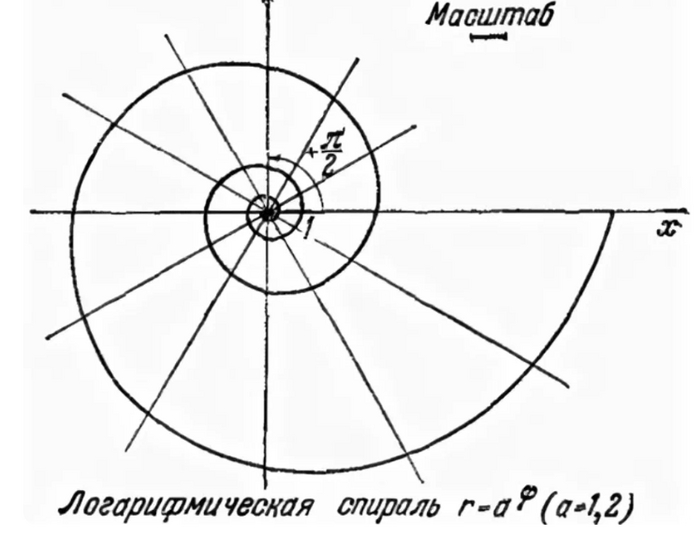
Так вот если туда запустить логарифм, получим нечто такое:

Такое расширение спирали логично. Ведь мы идём по лестнице не по одной ступеньке, а аж по степенной функции. Показатель степени изменяется на единичку, а значение прыгает в д-цать раз.

В общем-то, нам опять интересно тут другое. Подобным образом по какой-то только природе понятной логике растут, например, рога у барашка или формируются морские раковины. Само собой, в физике многих процессов присутствует логарифмическая спираль.

Ну а с вами был проект Инженерные знания. Мы делаем науку интересной :)