0 просмотренных постов скрыто
Шар идеальная фигура геометрии. Скуфский идеал. Золотое сечение
Показать полностью
1
Нерешаемая [мной] математическая задача о форме хлеба
Уже несколько лет во время завтрака меня периодически занимает одна математическая задача.
Я люблю мякоть хлеба, но не люблю корку.
Какой формы должен быть хлеб, чтобы мякоти было как можно больше, а корки - как можно меньше? Куб или шар?
Интуитивно понятно, что это должен быть шар.
Но интересует именно математически точное доказательство.
Если считать, что толщина корки пренебрежимо мала, а весь объем занимает мякоть, то задача сводится к следующей: у какой фигуры меньше площадь поверхности при равном объеме?
Другая формулировка: у какой фигуры больше объем при равной площади поверхности?
Попробовал найти решение, но безуспешно.
Приравнял площади поверхностей шара и куба, выразил оттуда сторону куба и радиус шара, потом подставил эти величины в формулы объемов шара и куба. Далее разделил получившуюся формулу объема шара на формулу объема куба. По идее, если результат больше единицы, то объем шара больше объема куба. Но у нас остаются неизвестные радиус и сторона куба, да и вообще в 4 часа ночи я уже плохо соображаю, поэтому хз что делать дальше.
Предлагайте ваши идеи в комментариях.
Показать полностью
3
Многомерные арбузы – пустая трата денег
Жарким летним вечером вы идёте домой, мечтая украсить ужин чем-нибудь освежающим. Вдруг словно со всех сторон разносится завлекающий голос со среднеазиатским акцентом – «Бери девятимерные арбузы, сладкие, как первая любовь!». Что ещё за девятимерные арбузы, задумываетесь вы на секунду. Но в такой жаркий день думать не хочется. Трёхмерные фильмы позволяют испытать больше ощущений, чем двумерные может и с арбузами также?
Вы небрежно протягиваете деньги в сторону непонятной формы ларька с фруктами. Они словно растворяются в пространстве, а взамен из ниоткуда появляется нечто, похожее на арбуз, хотя его размеры постоянно изменяются
Четырёхмерные шары ведут себя странно
-Как же мне его есть? – спрашиваете вы у продавца
-Так просто спроецируй на тарелку!
На удивление, девятимерный арбуз даже немного легче, чем привычный трёхмерный. В предвкушении необычного ужина, вы спешите домой. К сожалению, там вас ждёт разочарование: почти 77% арбуза составляет корка!
И это ещё хорошо, что арбуз был не 15-мерным. В таком мякоти меньше 9%. А в 30-мерном – меньше одного процента. Любопытное свойство многомерных шаров – их объём концентрируется у границы. В случае арбуза – у корки
Это кажется удивительным, но после несложных размышлений становится очевидным. Прежде чем их проделать, давайте вспомним, что такое шар. Возьмём какую-нибудь точку в пространстве – центр и число – радиус. Шар – это множество точек, лежащих на расстоянии не большем радиуса от центра. Теперь давайте представим, что арбуз – это идеальный шар. Как выглядит одномерный арбуз?
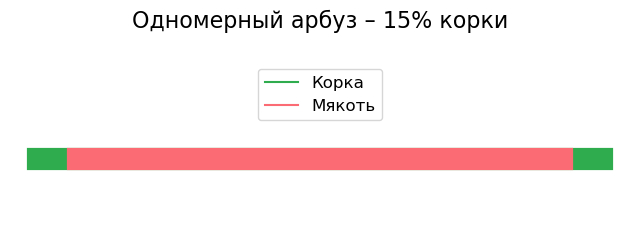
Если ходить разрешено только в одном измерении, то шар – это просто бесконечно тонкая линия длиной в 2 радиуса! Предположим, что корка занимает 15% её длины. Тогда арбуз будет выглядеть так:
Для наглядности я нарисовал линию пожирнее, но помните – одномерный арбуз не имеет толщины, только длину. Таким не наешься, но зато корка занимает всего 15%!
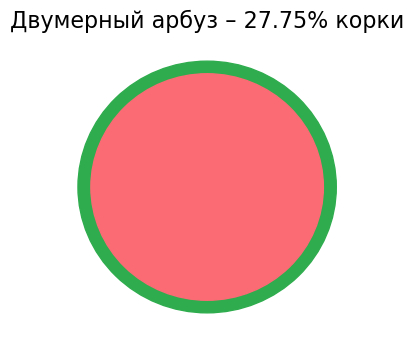
Как же будет выглядеть двумерный арбуз? Здесь тоже всё просто: шар с двумя измерениями – это знакомый всем круг
Из двумерных арбузов очень просто убирать косточки!
Вглядитесь в картинку: вместо двух небольших отрезков корка теперь выглядит как толстая окружность. Из-за размазанности по краям фигуры можно и не заметить, что она занимает почти 28% арбуза!
Трёхмерный арбуз, думаю, видели все. Корка огибает его со всех сторон, забирая ещё большую долю объёма. Если верно предположение, что она занимает 15% толщины, то почти 39% объёма уйдёт на корку. Больше трети стоимости арбуза составляет его несъедобная часть
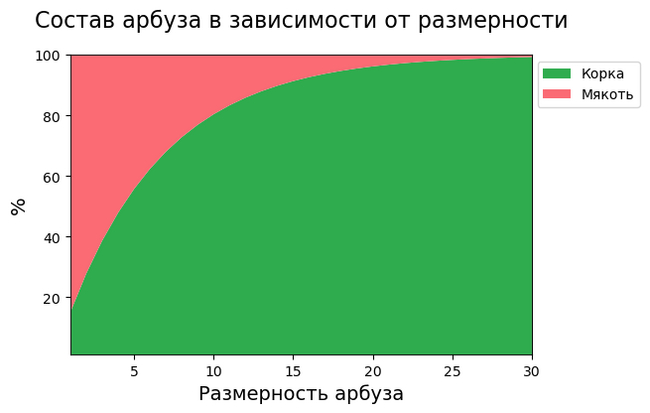
Дальше иллюстрации становятся сложнее, зато логика продолжает работать. Чем больше размерность арбуза, тем большая доля его объёма концентрируется у корки. При помощи математических формул, мы можем точно рассчитать процент:
В 30-мерном арбузе мякоти почти не остаётся: её там всего 0.76%. Девятимерный кажется уже не таким плохим, не так ли? Также любопытно, что, начиная с шестого измерения, объём арбуза уменьшается при фиксированном радиусе
Теперь когда вам в следующий раз будут предлагать купить многомерный арбуз, знайте – это невыгодно! Кушайте еду подходящей размерности
Показать полностью
3
Задача
Придумал, нечаянно, задачу и, сходу, решил ее не правильно.
Да, и вопрос - почему?
Показать полностью
1
Челлендж....так челлендж
Решил поддержать
