Насколько быстро остывает кофе?
Действительно ли бумажные термостаканы, в которых продают кофе на вынос в кофейнях, не дают напитку быстро остывать? Задумался и решил сравнить:
стеклянную пивную кружку на 0,5 л, в которую я обычно наливаю по утрам кофе;
кружку Starbucks - предположительно, с двойными стенками;
термостакан из ближайшей кофейни с крышкой.
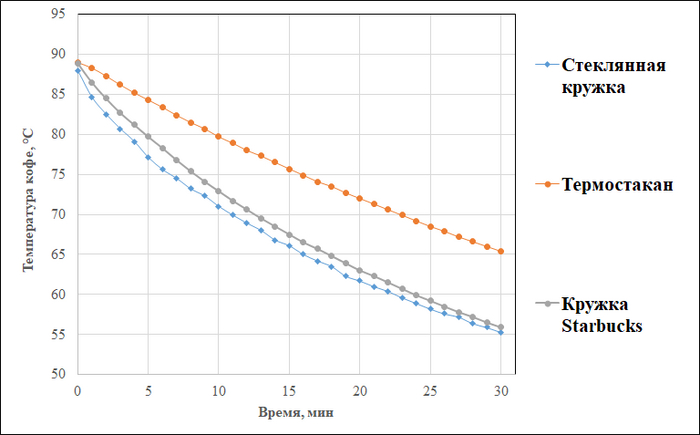
Для ЛЛ: в кружках сначала резкое снижение температуры, потом плавное остывание. В стакане сразу остывает плавно. Скорость остывания в кружках и стаканах после 10-15 минут одинаковая.
Ради такого дела взял с работы на вечер термометр, вот такой (- Тащ начальник, разреши любопытство потешить! Утром принесу! - Да на здоровье, только верни в целости). Заявленный диапазон температур от -50 до +150°С, погрешность ±0,2°С: температуру свежесваренного кофе перекрывает с гарантией, подходит идеально.
Как измерял: в течение получаса, с шагом 1 минута, записывал температуру, погружая щуп в жидкость примерно на 2/3, не касаясь им ни дна, ни стенок. Чтобы не держать термометр в руке, сделал из пластиковых обрезков и с помощью такой-то матери держатель. Температура в помещении - примерно одинаковая, 20-25°С. Как это выглядело:
Так как предполагается, что из такого стакана пьют через отверстие в крышке, то и измерение проводил с крышкой. Результаты представлены на графике ниже:
Красивое!
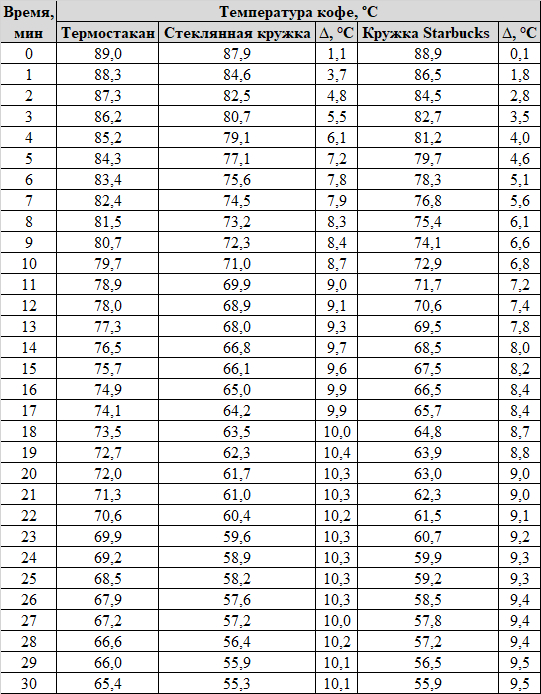
Казалось бы, очевидно: термостакан хорош. Но посмотрите на цифры:
Столбцы "дельта" - разница между температурой кофе относительно термостакана. После 10 минут эта разница, очевидно, начинает стабилизироваться, а после 15 - практически не изменяется: что в стеклянной кружке, что в кружке из старбакс. Отбросим точки до 15 минут и построим линии тренда по оставшимся данным:
Температура, как видим, во всех случаях убывает линейно: коэффициент корреляции близок к единице.
Обратите внимание на уравнения линий тренда. Линейная зависимость характеризуется уравнением вида y = bx+a, где а - свободный член линейной зависимости, а b - угловой коэффициент. Что это такое, с практической точки зрения? Если х (то есть время) равно нулю, y (температура кофе) = a, то есть "а" - это температура в гипотетический "начальный момент" времени. На графике это точка пересечения графика с осью ординат. Поскольку мы отбросили точки до 15 минут, естественно, линии тренда ведут не в область практически полученных значений температуры в нулевой точке, а ложатся ниже. Причём, что важно, для термостакана a = 85,7, что достаточно близко к реальной температуре в начале отсчёта (88,9), т.е. кофе в стакане остывает с самого начала практически с одной и той же скоростью. Можно предположить, что одной из возможных причин могут быть:
1) прогрев материала кружки в первые минуты после наливания кофе;
2) низкая теплоёмкость материала термостакана.
Логично - что охладит кофе сильнее? Холодная, толстостенная кружка, металл или довольно тонкий картон?
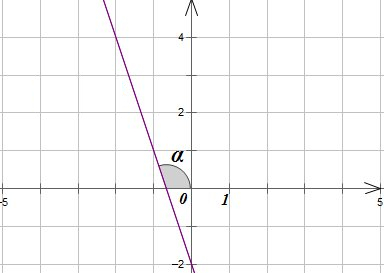
Теперь об угловом коэффициенте, или, иначе, тангенсе угла наклона прямой, в данном случае - линии тренда. О каком угле идёт речь, понятно из картинки ниже:
Если угол острый, коэффициент b > 0, а если тупой, как в нашем случае, то b < 0. Тангенс равен отношению противолежащего катета к прилежащему катету, то есть физически, применительно к нашим графикам, где по оси абсцисс отложено время, а по оси ординат - температура, это отношение температуры ко времени, то есть скорость остывания кофе!
d в таблице выше рассчитано в процентах относительно термостакана. Стеклянная кружка - практически один в один; кружка из Starbucks остывала чуть быстрее (видно на графике), но, в целом, разница не такая уж большая.
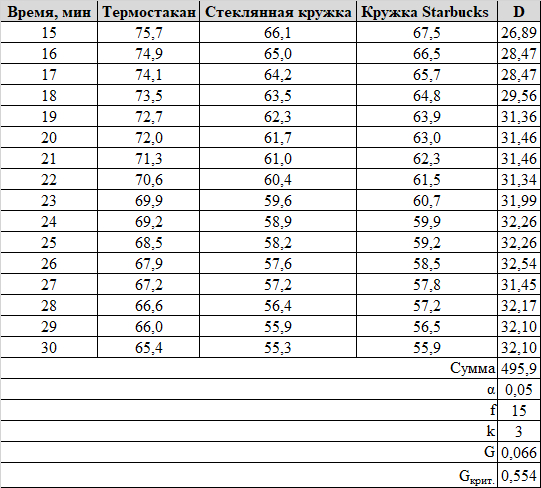
Проверим, являются ли полученные выборки на интервале 15-30 минут гомоскедастичными. Для этого рассчитаем дисперсию полученных значений температуры кофе в каждой временной точке после 15 минут (D) и критерий Кохрена (G), сравнив его с пороговым значением при уровне значимости 0,05 (Gкрит.):
Пример расчёта критерия Кохрена в Excel приведён здесь. Сравнивая расчетное значение G (0,066) с критическим значением G(0,05) = 0,554, приходим к выводу, что гипотеза о равенстве дисперсий для этих выборок не опровергается на уровне значимости = 0,05. То бишь, говоря человеческим языком, разброс измеренных значений температуры в каждой точке в интервале 15-30 минут примерно одинаковый, во что бы кофе ни был налит. Ба-дум-тс.
Что ещё можно отсюда вытянуть? Используя любезно рассчитанные Excel коэффициенты уравнений линейной регрессии (см. график с линиями тренда), можно рассчитать отклонение фактически полученного значения температуры в каждой точке от расчётного.
Ни в одной точке отклонение измеренного значения температуры не отличается от рассчитанного более, чем на 2%.
Т.о., для отрезка 15-30 минут температура кофе во всех случаях убывает строго линейно; это отмечается визуально, подтверждается крайней близостью коэффициента корреляции уравнений линейной регрессии к единице и хорошей корреляцией между рассчитанными значениями температуры (из уравнений линий тренда) и практически полученными. Угловые коэффициенты близки. Рассчитанный критерий Кохрена не превышает критического при уровне значимости 0,05, что также свидетельствует о равномерности остывания кофе в любой ёмкости после 15 минут.
Подведём итог. Через некоторое время скорость остывания выравнивается, вне зависимости от того, во что он налит, закрыта ёмкость или нет. Возможно, это связано с тем, что материал термостакана меньше охлаждает кофе в первые минуты после наливания. Так что в целом - да, в закрытом термостакане кофе дольше останется горячим, но не потому, что он лучше удерживает тепло.
P.S. Если где ошибся в расчётах и/или формулировках, прошу прощения.
P.P.S. Пока выполнял обсчёт, вспомнил машину Голдберга: