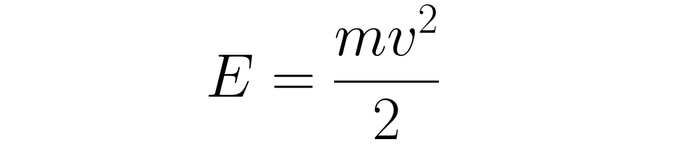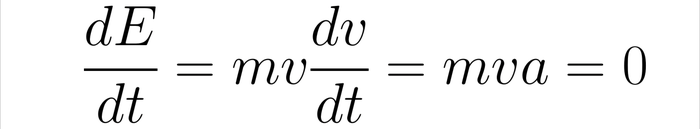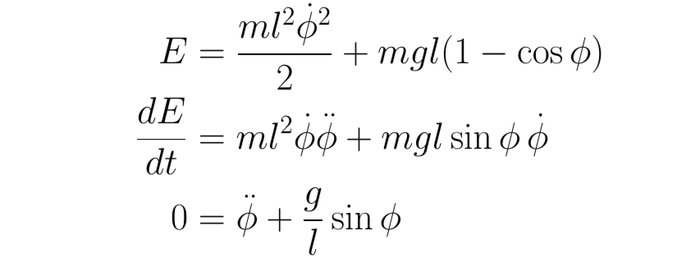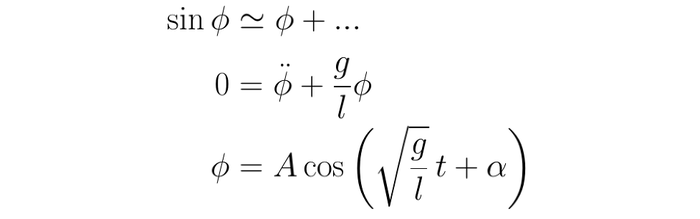learntheory
О симметриях в теоретической физике
В этом посте я попробую рассказать на общедоступном уровне о том, как теоретическое описание физических систем использует симметрии и законы сохранения. Под "общедоступным" уровнем я подразумеваю то, что рассказ ниже будет состоять из весьма упрощённых объяснений на примере механических систем. Эти объяснения я неоднократно использовал в общении со школьниками и младшими студентами.
Данный пост в некотором смысле пробный. Меня много раз просили рассказать о куда более запутанных материях, но без минимальных математических методов я вряд ли далеко уйду от банальной истории. Если пост зайдёт, то я попробую через несколько последовательных шагов дойти до простых вещей в физике частиц и ядерке.
Внимание! В посте будут формулы, возможно правильные.
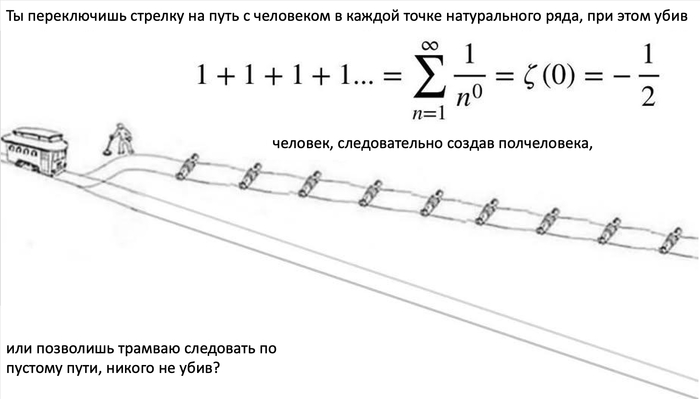
Для обсуждения симметрий нам придётся разобраться с тем как же работают все эти бесконечные приближения а ля сферический конь в вакууме
Несколько утрируя, с точки зрения теоретика любая задача должна быть разделена на понятные концептуально и простые технически шаги (keep task small), которые позже можно сгруппировать. А обобщить полное описание на сложную реальную систему "просто", только считать конкретные результаты будут уже не ручками на бумажке. Другими словами, сферический конь в вакууме не просто упрощение, а именно что ступенька для описания реальности. К этому мы ещё несколько раз вернёмся.
О каких симметриях обычно идёт речь в физике?
Вот несколько примеров:
1) Пустое пространство нашего мира однородно, проведя множество экспериментов в Питере и повторив их в Новосибе экспериментатор обнаружит, что результаты совпадают. Конечно же, предполагается, что эксперименты правильно поставлены -- мир однороден, когда он пуст. Поэтому нарушение однородности мусором окружающими предметами повлияет на результаты на каком-то уровне точности, но мы говорим про идеализацию;
2) В классической физике время опять же однородно -- эксперимент сейчас и через сто лет даст один и тот же результат, если конечно же сам объект изучения не меняется. Это снова идеализация пустой вселенной, где нитка у маятника не гниёт, а груз не ржавеет;
3) Пустое пространство изотропно -- в мире нет выделенных направлений. Стреляя из одной гром палки в двух разных направлениях, вы вполне ожидаете, что снаряд полетит одинаково, с точностью до "лишних" объектов на его пути, ветра, и прочих досадных осложнений;
4*) Кроме "внешних" координатных симметрий (время тоже координата), мы также часто встречаемся с "внутренними" симметриями, правда они скорее проявляются уже на квантовом уровне. Это выходит за рамки обсуждения в этом посте, но самый простой случай -- электрический заряд, сохранение которого связано с инвариантностью мира по отношению к некоторой фазе полей материи (калибровочная симметрия). Проще говоря, заряженные частицы описываются комплексными полями, что в свою очередь говорит о существовании соответствующих античастиц (комплексно сопряжённые поля);
Кроме того, что все описанные симметрии полагается обсуждать в пустом мире, они также могли бы нарушаться самой структурой нашей вселенной. Например, мы уже знаем, что даже в отсутствии большинства привычных нам объектов, однородность во времени сломана космологическим расширением. Более того, люди вполне серьёзно обсуждают существование оси зла -- некоторого выделенного направления на космологическом масштабе (прощай изотропность). Но опустим это до других постов, а пока продолжим разговор о классической физике.
Почему симметрии важны? Кроме наивного упрощения уравнений, описывающих какой-то конкретный случай, (почти) каждая симметрия позволяет завести новую сохраняющуюся величину. Это собственно суть теоремы Нётер, сама же Эмми (автор) на фото ниже тут могла бы быть ваша шутка про "смотрит как на ..."
А каждая сохраняющаяся величина заметно упрощает описание -- ведь удобно знать связь между разными величинами, которые иначе описываются системой сложных дифуров. Но тут у нас появляется небольшое осложнение. Как пишут на вики
Теорема обычно формулируется для систем, обладающих функционалом действия, и выражает собой инвариантность лагранжиана по отношению к некоторой непрерывной группе преобразований.
Бедные школьники пару раз нарывались и я объяснял им и этот шаг, но мы слишком стары для этого дерьма функционал действия это мягко говоря многовато математики для одного поста.
На картинке написано на эльфийском -- "Даже пятилетка смог бы понять это. Кто-нибудь сходите за ребёнком." (перевод художественный).
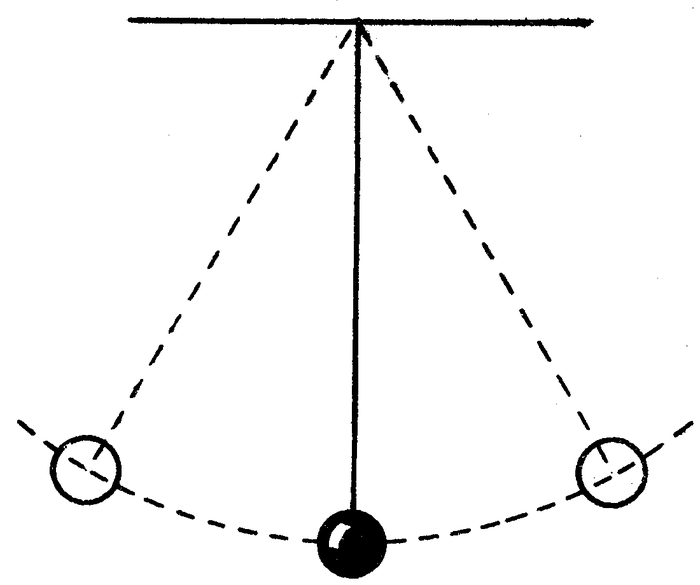
Поэтому у меня для вас ровно одна иллюстрация, которую можно понять несколькими способами, в зависимости от вашей испорченности вашего знания теормеха. И это, та-дам, маятник помноженный на закон сохранения энергии. Правда даже этой иллюстрации хватит, чтобы многие посчитали меня изварщенцем перестали читать, ибо ниже начнут появляться формулы. Хочу заметить, что я только что пообещал иллюстрировать вполне себе современный теорфиз с помощью двух самых часто встречаемых тем для школьных уроков физики. С другой стороны, это не удивительно, ведь, как говаривал кто-то из великих, работа теоретика это поиск всё новых применений для задачи о колебательной системе.
Но сначала нам будет полезно рассмотреть случай ещё проще -- точечную массу и никаких ниток. Для частицы в пустом пространстве энергия содержит только кинетический член, который всем хорошо знаком:
Хотя в более современных формулировках механики закон сохранения выводился бы через теорему Нётер, а описание системы начиналось бы с другого скалярного функционала, но нам сейчас это не так важно. Можете считать форму кинетического члена эмпирическим наблюдением. Важно же для нас то, что если энергия сохраняется, то это буквально означает, что она неизменна во времени (мир однороден по времени помните?), а значит
В случае одномерного движения, когда произведение между скоростью и её производной обычное (для векторов пришлось бы разбираться дольше), это эквивалентно одному из законов Ньютона -- если тело движется с постоянной скоростью в инерциальной системе отсчёта, то действующая на него сила равна нулю.
Вроде бы это очень простое наблюдение -- мы только что увидели, что закон сохранения энергии выполняется на ньютоновских уравнениях движения. Ну это там, где ускорение на массу равно силе, сил-то тут нет. С другой стороны, факт отсутствия сил оказывается равносилен (в одномерном случе) однородности мира -- в энергии нет вкладов зависящих от координаты точечной массы. Это самая простая известная мне иллюстрация применения симметрий мира для ограничения уравнений, описывающих систему! Более того, используя современные формулировки однородность мира приводит к закону сохранения импульса, что собственно мы с вами и пронаблюдали на примере выше.
Теперь мы можем перейти к математическому маятнику. Ситуация будет чуточку сложнее, пространство всё-таки перестало быть однородным, но однородность во времени осталась и мы снова будем использовать закон сохранения энергии. Сразу замечу, что математический маятник всё ещё одномерен -- движение описывается одним параметром (e.g. угол от вертикальной оси), но теперь параметр не является простой декартовой координатой. Я также опущу тривиальные шаги, которые заинтересованный в алгебре читатель легко сможет воспроизвести, а остальным они скорее всего будут мешать. Так как пикабу не имеет интерфейса, который дружил бы с техом, то вот вам немного формул одной картинкой, чтобы не копипастить каждую отдельно:
где точки отвечают производным по времени, фи с точкой -- угловая скорость, фи с двумя точками -- угловое ускорение, l -- длина нити, g -- ускорение свободного падения. Форма энергии в первой строчке совершенно обычна -- кинетический член для точечной массы, где скорость выражена через угловую скорость, помноженную на радиус окружности, плюс потенциальная энергия, которая становится тем больше, чем дальше фи от нуля (ноль = положение грузом вниз).
Если вы не узнали, то присмотритесь внимательнее и обнаружите, что перед вами уравнения для математического маятника, которое принимает форму привычного уравнения для гармонических колебаний в предположении о малости амплитуды оных (надо разложить синус).
Действительно, раскладываясь в ряд по малости аргумента (а без этого решение не выражается через элементарные функции) легко получить
где А -- амплитуда, а альфа -- постоянная фаза. Эти свободные параметры собственно задают начальные условия для маятника. Последняя строчка на скрине выше и есть математическая запись гармонических колебаний. Для тех, кто в жизни не видел как решается дифур, очень рекомендую воспринимать это как обратный факт -- можно проверить, что вторая производная от написанной функции пропорциональна самой функции с нужным коэффициентом, чтобы решить уравнение во второй строке.
Здесь нужно снова сделать несколько замечаний. Во-первых, может показаться, что ничего удивительного не случилось -- закон Ньютона в действии. Но нужно учитывать, что теперь задача живёт на плоскости, так что закон Ньютона, вообще говоря, записывается для векторных величин -- работать же со скалярной энергией значительно проще. В мою бытность школьником такой подход рассказывали на олимпиадных кружках, так как он позволяет решать весьма сложные колебательные системы. Поэтому теоретики так любят теорему Нётер и всякие дополнительные связи на свои системы. Во-вторых, мы снова видим, что зависимость энергии от координаты приводит к появлению силы, при этом производная энергии по (обобщённой) координате пропорциональна соответствующей (обобщённой) силе. Если координата угловая, то и сила будет моментом силы. В-третьих, мы убедились на более сложно примере, что формулировка движения одномерных систем через сохранение энергии, а значит в некотором определённом смысле через однородность мира во времени, работает.
Примерно в этом месте я выдохся, так что начну подводить итоги. Работая с более продвинутыми методами, симметрии задачи/мира становится всё проще использовать. Но важнее, что сами методы описания систем начинают базироваться на симметриях, которые позволяют придать физический смысл основным математическим объектам. Отчасти поэтому в теоретической физике так часто говорят о "красоте описания" и часто используют её в качестве руководящего принципа (теория должна быть красивой). Отсюда (из симметрий мира и теоретического описания) произрастает предсказание о существовании античастиц, здесь появляется проблема естественности в стандартной модели, и многое другое. Про всё это можно много и интересно рассказывать, было бы время и хватило бы идей, как минимизировать математическую сторону истории :)
В качестве бонуса для дочитавших -- ещё одна забавная картинка про сферического "коня" в вакууме, которую я в первый раз встретил в виде распечатки будучи с визитом в теоротделе в ЦЕРНе:
Ответ на пост «Азбука естествознания: большой адронный коллайдер»1
Был тут пост про LHC, тот который большой адронный коллайдер, и, видимо, мне придётся написать некоторый пост ответ -- сам напросился. Пост я попробую сделать более или менее полноценным, чтобы случайному читателю было тоже интересно, а к дополнительным причинам перейдём позже.
Пост из заголовка плох только тем, что несколько коротковат и содержит мало фактов о LHC. С другой стороны, про этот огромный эксперимент можно долго и интересно рассказывать, так что давайте сначала перечислим какие-то базовые факты, как это делают обычно во вступлении любого доклада для студентов.
Факты:
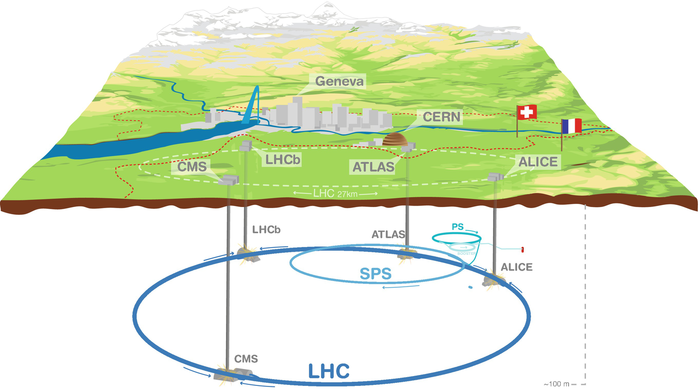
1) Картинка выше изображает стилизованную окружность коллайдера, длина 27км. Приятно, что на этой же картинке видно женевский международный аэропорт -- о масштабах судите сами;
2) Основная часть "игрушек" залегает глубоко под землёй -- где-то 175м, см. схему ниже:
3) Стоит это удовольствие на масштабе $10^10, а год работы обходится в $10^9, только на электричество у них уходит $20-30млн в год;
4) Для поворота заряженных частиц на окружности используют магнитные поля, собственно большая длина окружности (а значит и большой радиус) это цена за увеличение максимальной энергии частицы при максимальном доступном магнитном поле -- всё ещё лимитирующая технология. В LHC используют сверхпроводящие магниты при температуре около 2К (просто космос), а для этого гоняют где-то 150т жидкого гелия;
5) На этой установке чаще всего сталкивают протоны с протонами, но там также есть очень богатая программа по соударениям протонов с ядрами и ядер с ядрами;
6) Для иллюстрации происходящего на коллайдере хорошо понимать, что по окружности гоняют два пучка, в каждом летает почти 3к протонных "сгустков", разделённых пустотой. Это позволяет контролировать интенсивность столкновений.
6) Каждое такое "облако" содержит 10^11 протонов и имеет размер порядка 30см в длину и 1мм поперёк, хотя поперечный размер уменьшают в точках пересечения встречных пучков, чтобы повысить вероятность взаимодействия между протонами -- интенсивность "столкновений";
7) Энергия столкновения двух протонов 13 TeV (где-то 2*10^(-6)Дж), что примерно в 13к раз больше энергии покоя протона. Полная энергия в пучке колоссальна и примерно равна 350МДж, что близко к кинетической энергии сапсана (660т) при скорости 117км/ч, вот только концентрация там побольше :) Если развлекаться с тротиловым эквивалентом, то получится примерно 77кг;
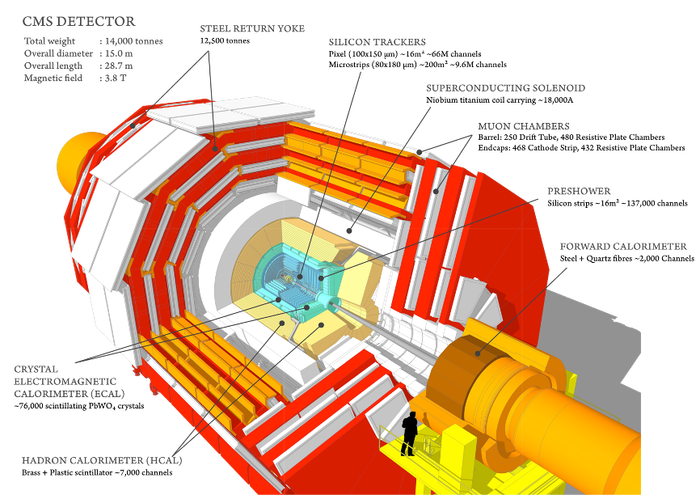
8) Разогнать и столкнуть протоны мало, так что кроме самого LHC люди долго и мучительно строили детекторы -- это отдельные эксперименты, которые собирают информацию о частицах, производимых в столкновениях. Ниже схема одного из детекторов (CMS), обратите внимание на человеческий силуэт, добавленный для масштаба:
9) Детектор видит где-то миллиард соударени протой в секунду, но столько информации становится трудно вывести, да и хранить невесело. Поэтому детекторы сохраняют примерно сто событий из миллиарда, которые имеют интересные сигнатуры. Даже после таких усилий поток информации там 1-5 GB/s, а отводить его надо из очень малой области, что целая проблема. Ниже типичное событие при соударении ядер, записанное детектором и красиво отображённой их же софтом, в ядерных столкновениях поток информации ещё выше:
Этот список можно долго продолжать, но я просто отправлю заинтересовавшихся сюда, сюда, и вот сюда, а сам перейду ко второй части.
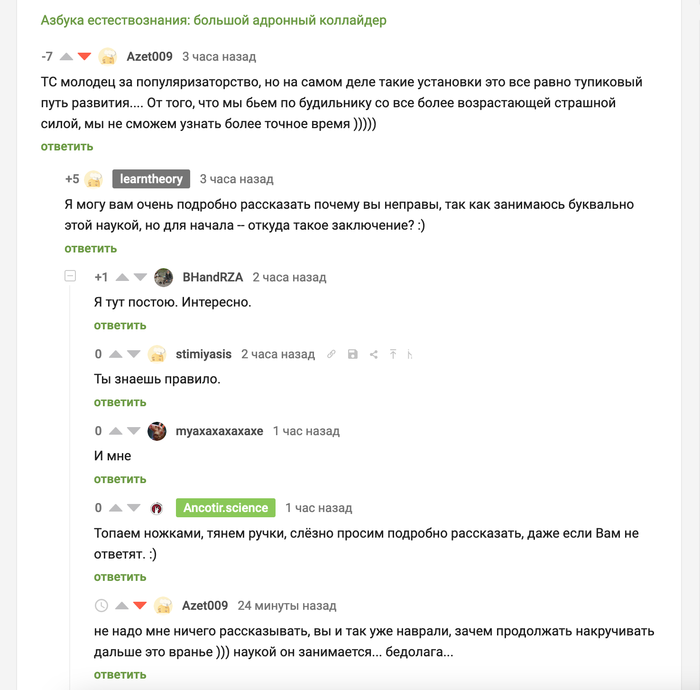
В посте из заголовка был комментарий -- не нужно, мол, таких установок, тупик в науке, нечего бить будильник, ну и сами смотрите:
ссылка на коммент тут. А я мимо проходил и подумал, что может быть стоит пояснить зачем собственно повышать энергии таких установок и как там устроена физика на микроскопическом уровне. Так как заинтересованных людей набралось достаточно много, хотя сам @Azet009 и решил, что я в чём-то уже вру (facepalm), то к этому и перейдём.
Зачем бить всё сильнее и что мы так узнаём:
I) Ударить игрушку об стену или две игрушки друг о друга один из первых экспериментальных опытов всех детей. Обычно из этого эксперимента дети узнают о том, что игрушку жалко а ремнём больно, что там было внутри, ну или насколько прочного материала были игрушки/стены. В физике элементарных частиц всё почти также, вот только мир у нас квантовый и экспериментаторам за это даже платят, так что вылететь может что-то новое, чего не было внутри наших игрушек.
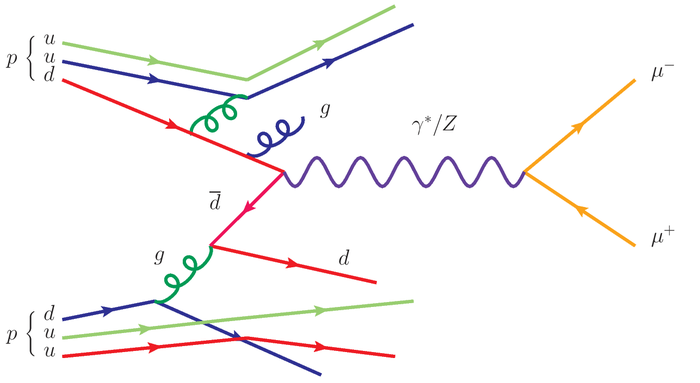
Ниже схематическое изображение (диаграмма Фейнмана) одного из множества возможных взаимодействий двух протонов:
Цветные ровные линии -- фермионы, на данной диаграмме представлены кварками (u, d) и мюоном (антимюоном). Пружинки изображают глюоны, которые являются переносчиками ядерных взаимодействий. Волнистая линия -- виртуальный фотон или Z-бозон, переносчики электромагнитного и слабого взаимодействий соответственно.
Слово "виртуальные" отвечает тому, что это не обычные частицы/волны, а некоторые квантовые состояния, которые не могут существовать долго. На примере фотона -- это фотон у которого импульс и энергия такие, словно он имеет массу (помните, что фотоны обычно безмассовые?), и поэтому он очень быстро распадается на что-то с удобоваримыми свойствами. В данном случае виртуальный фотон распадается на мюон-антимюонную пару.
Если такой процесс случился на LHC, а у него есть вполне определённая вероятность, которую даже не очень-то и сложно посчитать, то детекторы зафиксируют какие-то адроны и мюон/антимюон. Адроны получатся потому, что кварки и глюоны не могут оставаться свободными из-за так называемого невылетания цвета, но про это можно написать целую серию отдельных постов. Тем более квантовая хромодинамика (КХД), ответственная за взаимодействия цветных частиц, моя основная специализация. Но для нас сейчас важно, что получилась пара мюон-антимюон, которой не было в классическом составе изначальных протонов. Эти мюоны и есть те "квантовые куски" о которых я говорил, сравнивая ситуацию с разбиванием игрушек. Как если бы мы кинули будильник о стену, а из его осколков вылетел жираф.
II) Полагаю теперь понятно, что если "бить будильник", то можно найти что-то новое. Но зачем бить всё сильнее? Тут всё прозаично -- взаимодействия протонов, рождающие новые частицы, ограничены в своей возможности передать энергию в конечное состояние. Если всю энергию столкновения перевести в пару каких-то неизвестных нам частиц, то массы частиц будут ограничены половиной этой самой энергии в 13TeV. (В этой науке принято класть скорость света единицей (с=1) и измерять массу покоя энергией)
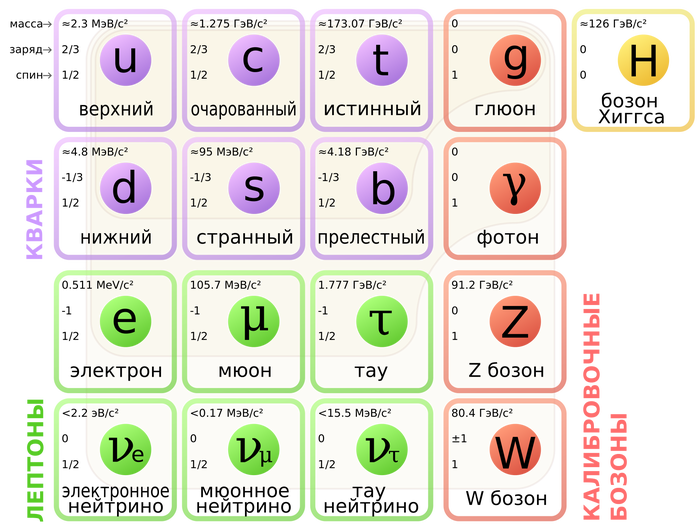
Более того, такие тяжёлые частицы не живут долго, а значит надо ещё и понять по их продуктам распада, что там что-то такое было. Для этого нужно собрать большой набор "подозрительных" событий, которые скорее всего редки. А события, где вся энергия протонов перешла в пару, можно считать вовсе не вероятными. Вот и получается, что мы весьма ограничены в поиске новых тяжёлых частиц. Ясное дело почти все "лёгкие" частицы мы уже довольно давно нашли и построили неплохую модель "всех" элементарных частиц, которую чаще всего называют просто стандартной моделью. Вот вам текущий набор частиц, которые нужны, чтобы описать наблюдаемый мир (почти):
III) А зачем искать тяжёлые частицы, если мы всё так неплохо объясняем тем, что уже и так есть? Ну, во-первых, хиггса нашли только на LHC, его как раз и не хватало. Во-вторых, мы знаем, что стандартная модель не совсем полна. Например, в неё не вписываются массы нейтрино, а они есть, в ней не хватает тёмной материи, в ней мог бы быть аксион, в неё не вписывается гравитация... Да, тёмная материя может состоять не из новых частиц, а из каких-то экзотических состояний тех, что уже в списке. Мы такие состояния пока не видим, и их всё равно надо найти и понять. Да, проблемы, решаемые аксионом, вероятно можно решить как-то иначе, скорее всего заметно сложнее, но это открытый вопрос. Ну а главное, мы всё равно видим, что в теории есть места, где концы с концами не сходятся.
Замечание: Конечно мир может оказаться проще и искать нужно совсем немного, но это уже философские вопросы о познаваемости, смысле познавать, целях человечества и человека. Короче, это довольно скучное обсуждение, которое сводится к вкусовщине -- любая философская система строится на каких-то аксиоматических постулатах. Ожидаемые же изменения в теории, скорее глобальны.
IV) Кроме поиска новых частиц, мы всё ещё многое не понимаем про старые, и вот это куда более важная задача LHC, хотя её и меньше рекламируют.
Типичный пример -- мы не понимаем, как кварки и глюоны собираются в протоны, а те, в свою очередь, в ядра. При этом описывать кварки и глюоны при высоких энергиях мы умеем весьма неплохо, но вот дальше беда -- теория нелинейна при энергиях ниже. Более того, моделируя КХД на супер-пупер компьютерах, мы видим это нелинейное поведение, то есть теория работает, но мы не понимаем как!
В частности, для изучения этой проблемы на LHC смотрят не только на столкновения протонов, но и на столкновения ядер, что позволяет производить многочастичное состояние, которое состоит из большого числа кварков и глюонов -- кварк-глюонная плазма (КГП). Полученные капли этой материи, настолько горячи -- пара триллионов градусов, что цветные частицы летают там свободно. Это происходит потому, что характерные термальные энергии каждой частицы выше точки конденсации в адроны. Наблюдая за тем, как эта материя остывает мы можем понять очень многое о том, как работает КХД. Опять же про КГП я могу очень долго писать, но это тема для другого поста.
V) Закончу этот список я следующим замечанием -- повышая энергию мы изучаем поведение мира на всё меньших дистанциях. В этом смысле коллайдеры работают как микроскопы, которые могут произвести всё более коротковолновые (высокоэнергетические) лучи, чтобы посмотреть на содержание всё более маленьких объектов.
Связь длины волны с разрешением довольно часто встречается -- это и дифракционный предел, который по сути сидит в показателе экспоненты плоской волны, и соотношение неопределённости. Действительно, если на размер изучаемого объекта приходится меньше одной длины волны, то его замылит. Так что, чтобы проверить элементарен ли тот же хиггс его надо потрясти на масштабе сравнимом с его размером.
PS: Не бейте сильно за грамматику, я очень редко пишу по-русски...
PPS: На всякий случай -- всё взято из моей собственной недавней презентации для студентов :) Картинки честно украдены из тырнетов, ставить ссыли на источники картинок совсем лень.
До сообщества достучаться не вышло...
И станут минусы плюсами...
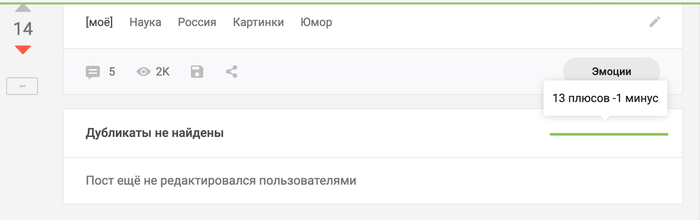
Я тут вчера нарвался на аномалию на пикабу и спешу поделиться! Кто ещё помнит школьную программу по математике? Минус отрицательное число даёт плюс, не правда ли?
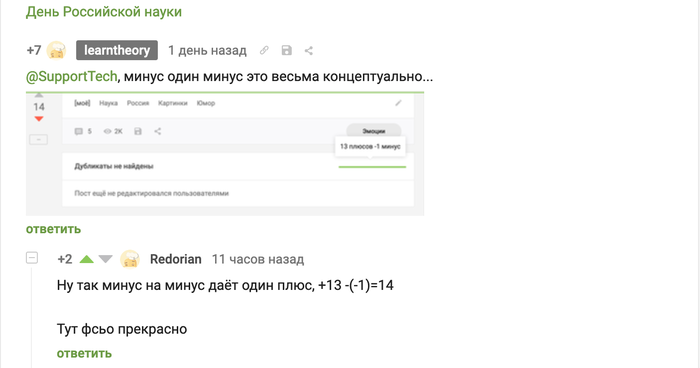
Как вам? Рейтинг поста отображается как 14, у поста 13 плюсов и -1 минус, что в целом отлично складывается...
Ссылка на коммент (и пост), кому интересно. Стоит заметить, что @Redorian явно помнит как работает математика!
Короче говоря, общие правила арифметики, а может быть даже алгебры, работают на пикабу! И даже баги им подчиняются... :)
PS: Минус мой, баг видимо тоже мой, так что пусть будет моё.
PPS: СаппортТех ответил, но видимо там не поняли вопрос...
Ответ на пост «Наглядно»2
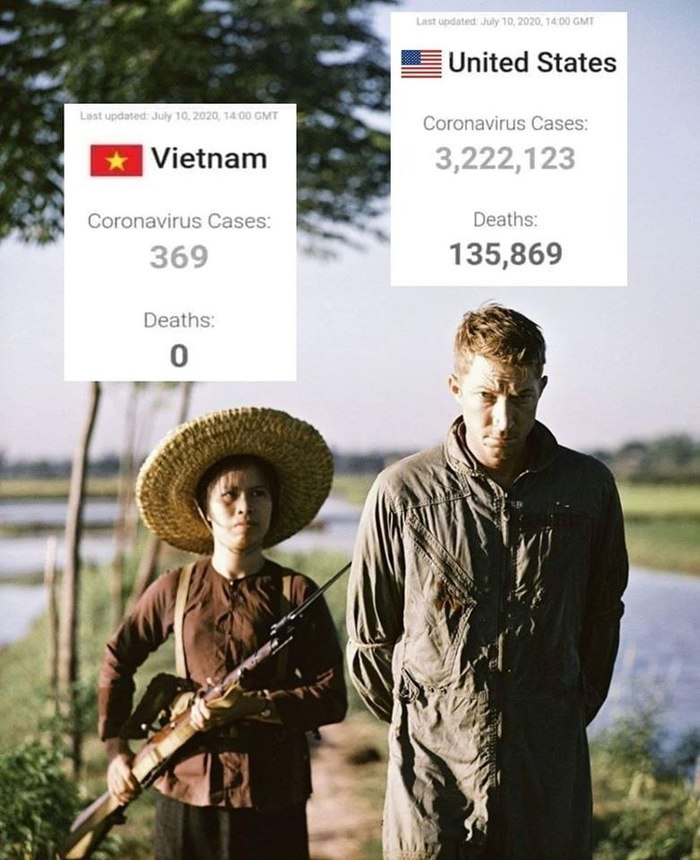
(картинка из оригинального поста)
Хочу привести заметку в буке со странице моего коллеги, профессора в Chicago U. и вьетнамца по национальности -- почему во Вьетнаме всё так хорошо с короной.
Перевод мой:
Бывший посол Франции во Вьетнаме пишет из больничной палаты в Ханое:
"...Госпитали не перегружены и входящий и исходящий потоки пациентов находятся под контролем. Вы можете поверить мне. Я пишу из палаты номер 541 Ханойского госпиталя тропических заболеваний, в который поступают все зарегистрированные случаи. Мой тест на вирус оказался позитивным после двух недель в Париже, и я был направлен в госпиталь в 2 часа утра 25го марта. У меня не появилось никаких симптомов, я не болен, но останусь в госпитале до тех пор, пока мой тест не будет отрицательным. Я заключён в госпитале, но это не для моего блага, а для общества, которое необходимо защищать от заражения. Отправить пациента с положительным тестом и без симптомов домой, тем более без маски, кажется невозможным здесь. Во Вьетнаме защита общества всегда первична. Моя личная свобода может подождать. Личность ничто -- общество всё! Вьетнамская стратегия борьбы с вирусом проста и беспечно посягает на неприкосновенность частной жизни. Любой заражённый человек (обозначаемый как F0) должен немедленно предоставить информацию о личностях всех людей, с которыми он контактировал (обозначаются F1) и список всех мест, которые посещал, в предшествующие дни. Я сделал тоже самое в ночь с 24го на 25е марта перед отправлением в госпиталь. И лучше вам не врать в этом деле. Система наблюдения за популяцией, свойственная коммунистическому режиму и работающая с 1954 года на севере и с 1975 на юге, раскроет малейший секрет и мгновенно накажет, во имя обеспечения безопасности общественного здоровья. Люди, с кем контактировал больной, F1, немедленно отправляются в закрытые центры или на самоизоляцию дома на 14 дней. Каждый F1 обязан уведомить всех людей с кем он контактировал последнее время. Эти люди обозначаются F2. F2 заплатят тем, что будут вынуждены дополнительно соблюдать социальную дистанцию и по возможности самоизолироваться на 14 дней. На 4е апреля 2020го более 73000 людей находятся на карантине, более 40% в закрытых центрах, часто управляемых военными, или дома, или в госпиталях.
Если кто-то из группы F1 оказывается заражённым, то этот же процесс повторяется. Все F2 превращаются в F1, и отправляются на тестирование и самоизоляцию, и так далее. Эта пирамидальная работа над контролем за инфицированными людьми и группами риска выглядит титанической или муравьиной в зависимости от вашего выбора. Это возможно не только потому, что Вьетнам коммунистическая страна, обладающая системой наблюдения за обществом. Южная Корея и Япония, плюралистические демократии, используют похожие по духу методы контроля популяции. Если такие подходы и процедуры работают для почти 100 млн жителей, то это просто потому, что они одобряются и применяются всем населением. Во Вьетнаме, как и в Японии, Корее и Китае, это согласие в пользу таких ограничивающих методов базируется на самой культуре цивилизации этих стран. В конфуцианском мире, во Вьетнаме, как и в Корее, в Японии, как и в Китае, защита общества и его интересы преобладают над правами личности. Каждый принимает необходимость отправиться на карантин в военный лагерь 30 км от дома без вздрагивания, потому что эта жертва рассматривается как необходимая для общественного здоровья и защиты общества. Отказ -- не допустим...
Оригинал из поста на английском (переведён с французского переводчиком):
Former ambassador of France in Vietnam writes from his hospital room in Hanoi [google translate]:
"...The hospitals are not overwhelmed and the flow of patients, inbound and outbound, is under control. You can take my word for it. I am writing to you from room 541 of the Hanoi Tropical Diseases Hospital, which gathers all the cases detected. Tested positive for the virus after two weeks in Paris, I was transferred to the hospital at 2 a.m. on March 25. I have not developed any symptoms, am not sick, but will remain in the hospital until I become negative again. If I am confined to the hospital, it is not for me, but for the community that must be protected from my contagiousness. Sending home, moreover without mask, a patient diagnosed positive but without serious physical problem, is unimaginable here. In Vietnam, group protection takes precedence over any other consideration. My individual freedom can wait. The individual is nothing, the group is everything! Vietnamese strategy to deal with the virus is simple and blithely encroaches on privacy. Any contaminated person (the F0) must immediately give the identity of all the people he has encountered (the F1) in the previous days and list all the places he went to. I did it myself, on the night of March 24-25, before I left for the hospital. And better not lie. The system of supervision of the population, a consubstantial of the communist regime in place since 1954 in the north and 1975 in the south, will flush out the slightest secret and could blame you swiftly, in the name of protecting public health. The people in contact, the F1, are sent immediately for two weeks to a closed center or at home and tested. Each F1 is obliged to notify the people with whom it has been in contact. These are the F2. Price for F2: social distancing and if possible confinement at home for 14 days. As of April 4, 2020, more than 73,000 people were under quarantine, more than 40% in a closed center often run by the military, or at home or in the hospital. If one of the F1s proves positive, same thing again. All its F2 then become F1, are sent in turn to quarantine and tested. And so on. This pyramid monitoring work of the infected and at risk population is either a titanic or ant work depending on your choice. It is not only possible because Vietnam is a communist country endowed with a network of close supervision of the population. South Korea and Japan, pluralist democracies, have used similar monitoring methods in spirit. If this policy works and produces results for a population of almost 100 million inhabitants, it is simply because it is approved and applied by the entire population.In Vietnam as in Japan, Korea or the Chinese countries, this consensus in favor of such intrusive methods is based on a fundamental cultural and civilizational fact. In the Confucian world, in Vietnam as in Korea, in Japan as in the Chinese world (China, Taiwan, Hong-Kong, Singapore), the defense and interests of the group prevail over the rights of the individual. Everyone accepts without flinching to leave for two weeks in quarantine in a military camp thirty kilometers from home because this sacrifice is considered by all to be necessary for public health and the defense of the whole community. Refuse is simply not an option..."
Оригинальная статья на французском. Замечания про ошибки приветствуются, пишу с тапка, а в школе любил математику и физику.
Ответ на пост «Патент»1
Прочитал про мышеловку с револьвером и вспомнилось. Заезжал тем летом к коллеге в гости, а у него большой участок в пригороде Санта Фе, что в Нью Мексико (соседний с Техасом штат). Там большинство соседей фермы или ранчо держат, а у него просто дом с фруктовым садом. Так вот он рассказал, что завелись у него кроты, а выводить их ещё то развлечение. Он решил спросить соседей как с ними бороться, таки фермеры местные.
Приведу краткую версию ньюмексиканского метода борьбы с грызунами:
1) Ставишь ящик пива, заводишь гриль, зовёшь соседей — каждый приходит с ружьём и/или пивом.
2) Подгоняют чей-нибудь пикап, шлангом присоединяют к ближайшей норе.
3) К моменту когда все уже чуть выпили из кротового газенвагена лезут бедные животные, которые теперь и убежать не особо могут.
4) Все соседи дружно играют в тир, тем более мало кто успевает ездит на охоту, а так хоть ружьё пригодится. Кстати стрелять в их ебенях на своей земле можно, это не город.
Коллега сказал, что ему жалко зверушек — лучше уж их ядом и вибрацией. Пусть не так эффективно, зато никаких кровавых зрелищ.
Так что мышеловка с револьвером здесь вполне себе вписывается в культурные особенности.
Белка Аберта
На волне карантина в нашей деревне прибавилось дикой живности, что не обошло стороной и мой задний двор. Пушистую зданицу милаху было решено прикормить и заснять.
В гугле меня пока не банили и мне удалось выяснить, что это белка Аберта, широко распространённая в местных краях. А заодно прояснились ттх зверя, который как оказывается не особо запасает еду в отличие от своей дальней родни, набивающей щёки пока шкура не треснет. Так что перетаскав несколько орехов белк решил повысить эффективно и ныкать еду не отходя от кассы.
PS: Снимал на тапок gopro придавленный камнем к подставке под горшок (видно в кадре).