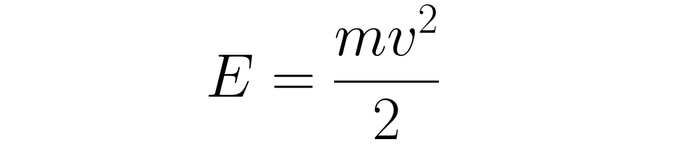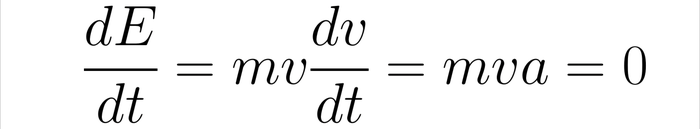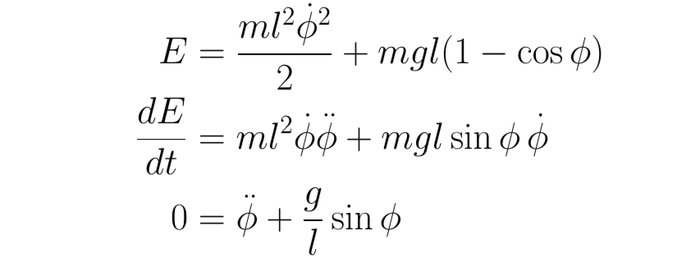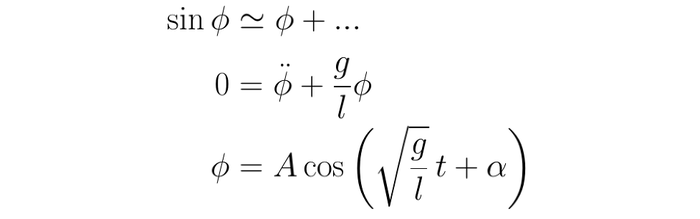О симметриях в теоретической физике
В этом посте я попробую рассказать на общедоступном уровне о том, как теоретическое описание физических систем использует симметрии и законы сохранения. Под "общедоступным" уровнем я подразумеваю то, что рассказ ниже будет состоять из весьма упрощённых объяснений на примере механических систем. Эти объяснения я неоднократно использовал в общении со школьниками и младшими студентами.
Данный пост в некотором смысле пробный. Меня много раз просили рассказать о куда более запутанных материях, но без минимальных математических методов я вряд ли далеко уйду от банальной истории. Если пост зайдёт, то я попробую через несколько последовательных шагов дойти до простых вещей в физике частиц и ядерке.
Внимание! В посте будут формулы, возможно правильные.
Для обсуждения симметрий нам придётся разобраться с тем как же работают все эти бесконечные приближения а ля сферический конь в вакууме
Несколько утрируя, с точки зрения теоретика любая задача должна быть разделена на понятные концептуально и простые технически шаги (keep task small), которые позже можно сгруппировать. А обобщить полное описание на сложную реальную систему "просто", только считать конкретные результаты будут уже не ручками на бумажке. Другими словами, сферический конь в вакууме не просто упрощение, а именно что ступенька для описания реальности. К этому мы ещё несколько раз вернёмся.
О каких симметриях обычно идёт речь в физике?
Вот несколько примеров:
1) Пустое пространство нашего мира однородно, проведя множество экспериментов в Питере и повторив их в Новосибе экспериментатор обнаружит, что результаты совпадают. Конечно же, предполагается, что эксперименты правильно поставлены -- мир однороден, когда он пуст. Поэтому нарушение однородности мусором окружающими предметами повлияет на результаты на каком-то уровне точности, но мы говорим про идеализацию;
2) В классической физике время опять же однородно -- эксперимент сейчас и через сто лет даст один и тот же результат, если конечно же сам объект изучения не меняется. Это снова идеализация пустой вселенной, где нитка у маятника не гниёт, а груз не ржавеет;
3) Пустое пространство изотропно -- в мире нет выделенных направлений. Стреляя из одной гром палки в двух разных направлениях, вы вполне ожидаете, что снаряд полетит одинаково, с точностью до "лишних" объектов на его пути, ветра, и прочих досадных осложнений;
4*) Кроме "внешних" координатных симметрий (время тоже координата), мы также часто встречаемся с "внутренними" симметриями, правда они скорее проявляются уже на квантовом уровне. Это выходит за рамки обсуждения в этом посте, но самый простой случай -- электрический заряд, сохранение которого связано с инвариантностью мира по отношению к некоторой фазе полей материи (калибровочная симметрия). Проще говоря, заряженные частицы описываются комплексными полями, что в свою очередь говорит о существовании соответствующих античастиц (комплексно сопряжённые поля);
Кроме того, что все описанные симметрии полагается обсуждать в пустом мире, они также могли бы нарушаться самой структурой нашей вселенной. Например, мы уже знаем, что даже в отсутствии большинства привычных нам объектов, однородность во времени сломана космологическим расширением. Более того, люди вполне серьёзно обсуждают существование оси зла -- некоторого выделенного направления на космологическом масштабе (прощай изотропность). Но опустим это до других постов, а пока продолжим разговор о классической физике.
Почему симметрии важны? Кроме наивного упрощения уравнений, описывающих какой-то конкретный случай, (почти) каждая симметрия позволяет завести новую сохраняющуюся величину. Это собственно суть теоремы Нётер, сама же Эмми (автор) на фото ниже тут могла бы быть ваша шутка про "смотрит как на ..."
А каждая сохраняющаяся величина заметно упрощает описание -- ведь удобно знать связь между разными величинами, которые иначе описываются системой сложных дифуров. Но тут у нас появляется небольшое осложнение. Как пишут на вики
Теорема обычно формулируется для систем, обладающих функционалом действия, и выражает собой инвариантность лагранжиана по отношению к некоторой непрерывной группе преобразований.
Бедные школьники пару раз нарывались и я объяснял им и этот шаг, но мы слишком стары для этого дерьма функционал действия это мягко говоря многовато математики для одного поста.
На картинке написано на эльфийском -- "Даже пятилетка смог бы понять это. Кто-нибудь сходите за ребёнком." (перевод художественный).
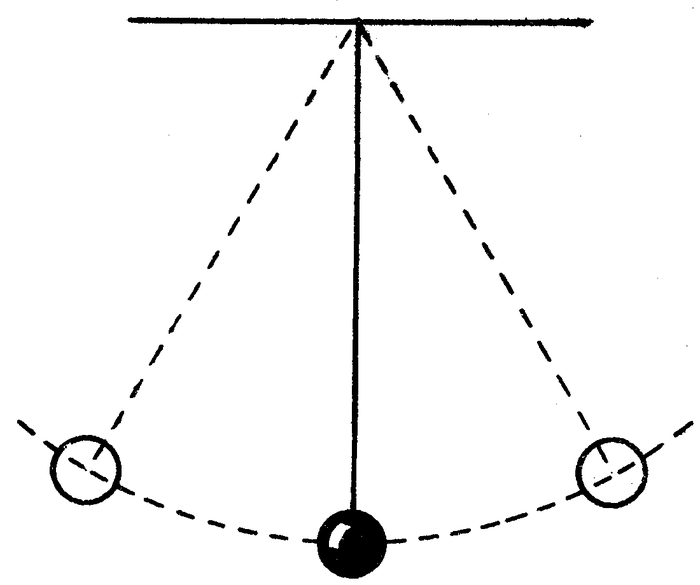
Поэтому у меня для вас ровно одна иллюстрация, которую можно понять несколькими способами, в зависимости от вашей испорченности вашего знания теормеха. И это, та-дам, маятник помноженный на закон сохранения энергии. Правда даже этой иллюстрации хватит, чтобы многие посчитали меня изварщенцем перестали читать, ибо ниже начнут появляться формулы. Хочу заметить, что я только что пообещал иллюстрировать вполне себе современный теорфиз с помощью двух самых часто встречаемых тем для школьных уроков физики. С другой стороны, это не удивительно, ведь, как говаривал кто-то из великих, работа теоретика это поиск всё новых применений для задачи о колебательной системе.
Но сначала нам будет полезно рассмотреть случай ещё проще -- точечную массу и никаких ниток. Для частицы в пустом пространстве энергия содержит только кинетический член, который всем хорошо знаком:
Хотя в более современных формулировках механики закон сохранения выводился бы через теорему Нётер, а описание системы начиналось бы с другого скалярного функционала, но нам сейчас это не так важно. Можете считать форму кинетического члена эмпирическим наблюдением. Важно же для нас то, что если энергия сохраняется, то это буквально означает, что она неизменна во времени (мир однороден по времени помните?), а значит
В случае одномерного движения, когда произведение между скоростью и её производной обычное (для векторов пришлось бы разбираться дольше), это эквивалентно одному из законов Ньютона -- если тело движется с постоянной скоростью в инерциальной системе отсчёта, то действующая на него сила равна нулю.
Вроде бы это очень простое наблюдение -- мы только что увидели, что закон сохранения энергии выполняется на ньютоновских уравнениях движения. Ну это там, где ускорение на массу равно силе, сил-то тут нет. С другой стороны, факт отсутствия сил оказывается равносилен (в одномерном случе) однородности мира -- в энергии нет вкладов зависящих от координаты точечной массы. Это самая простая известная мне иллюстрация применения симметрий мира для ограничения уравнений, описывающих систему! Более того, используя современные формулировки однородность мира приводит к закону сохранения импульса, что собственно мы с вами и пронаблюдали на примере выше.
Теперь мы можем перейти к математическому маятнику. Ситуация будет чуточку сложнее, пространство всё-таки перестало быть однородным, но однородность во времени осталась и мы снова будем использовать закон сохранения энергии. Сразу замечу, что математический маятник всё ещё одномерен -- движение описывается одним параметром (e.g. угол от вертикальной оси), но теперь параметр не является простой декартовой координатой. Я также опущу тривиальные шаги, которые заинтересованный в алгебре читатель легко сможет воспроизвести, а остальным они скорее всего будут мешать. Так как пикабу не имеет интерфейса, который дружил бы с техом, то вот вам немного формул одной картинкой, чтобы не копипастить каждую отдельно:
где точки отвечают производным по времени, фи с точкой -- угловая скорость, фи с двумя точками -- угловое ускорение, l -- длина нити, g -- ускорение свободного падения. Форма энергии в первой строчке совершенно обычна -- кинетический член для точечной массы, где скорость выражена через угловую скорость, помноженную на радиус окружности, плюс потенциальная энергия, которая становится тем больше, чем дальше фи от нуля (ноль = положение грузом вниз).
Если вы не узнали, то присмотритесь внимательнее и обнаружите, что перед вами уравнения для математического маятника, которое принимает форму привычного уравнения для гармонических колебаний в предположении о малости амплитуды оных (надо разложить синус).
Действительно, раскладываясь в ряд по малости аргумента (а без этого решение не выражается через элементарные функции) легко получить
где А -- амплитуда, а альфа -- постоянная фаза. Эти свободные параметры собственно задают начальные условия для маятника. Последняя строчка на скрине выше и есть математическая запись гармонических колебаний. Для тех, кто в жизни не видел как решается дифур, очень рекомендую воспринимать это как обратный факт -- можно проверить, что вторая производная от написанной функции пропорциональна самой функции с нужным коэффициентом, чтобы решить уравнение во второй строке.
Здесь нужно снова сделать несколько замечаний. Во-первых, может показаться, что ничего удивительного не случилось -- закон Ньютона в действии. Но нужно учитывать, что теперь задача живёт на плоскости, так что закон Ньютона, вообще говоря, записывается для векторных величин -- работать же со скалярной энергией значительно проще. В мою бытность школьником такой подход рассказывали на олимпиадных кружках, так как он позволяет решать весьма сложные колебательные системы. Поэтому теоретики так любят теорему Нётер и всякие дополнительные связи на свои системы. Во-вторых, мы снова видим, что зависимость энергии от координаты приводит к появлению силы, при этом производная энергии по (обобщённой) координате пропорциональна соответствующей (обобщённой) силе. Если координата угловая, то и сила будет моментом силы. В-третьих, мы убедились на более сложно примере, что формулировка движения одномерных систем через сохранение энергии, а значит в некотором определённом смысле через однородность мира во времени, работает.
Примерно в этом месте я выдохся, так что начну подводить итоги. Работая с более продвинутыми методами, симметрии задачи/мира становится всё проще использовать. Но важнее, что сами методы описания систем начинают базироваться на симметриях, которые позволяют придать физический смысл основным математическим объектам. Отчасти поэтому в теоретической физике так часто говорят о "красоте описания" и часто используют её в качестве руководящего принципа (теория должна быть красивой). Отсюда (из симметрий мира и теоретического описания) произрастает предсказание о существовании античастиц, здесь появляется проблема естественности в стандартной модели, и многое другое. Про всё это можно много и интересно рассказывать, было бы время и хватило бы идей, как минимизировать математическую сторону истории :)
В качестве бонуса для дочитавших -- ещё одна забавная картинка про сферического "коня" в вакууме, которую я в первый раз встретил в виде распечатки будучи с визитом в теоротделе в ЦЕРНе: