Глава 1. Постановка задачи и исходный язык

1. Зачем вводить двухполярную гравитацию

Цель двухполярной гравитации — построить строго определённый, воспроизводимый канал описания тяготения, в котором:

• исходными «кирпичами» являются полярность, графовая геометрия (как носитель связности) и правила вывода;

• гравитация понимается не как «сущность» и не как метафора, а как ориентация движения по потенциалу и как операциональная процедура вычисления поля;

• любая привязка к системе единиц СИ оформляется как калибровка моста, а не как «вывод константы природы из аксиом».

Здесь принципиальна дисциплина формулировок: двухполярный канал описывает то, что он действительно описывает, и не притворяется тем, чем не является.

2. Полярность как первичный механизм направления

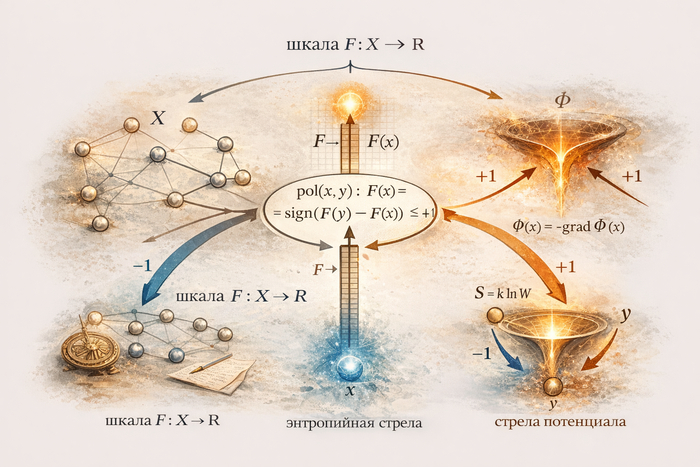
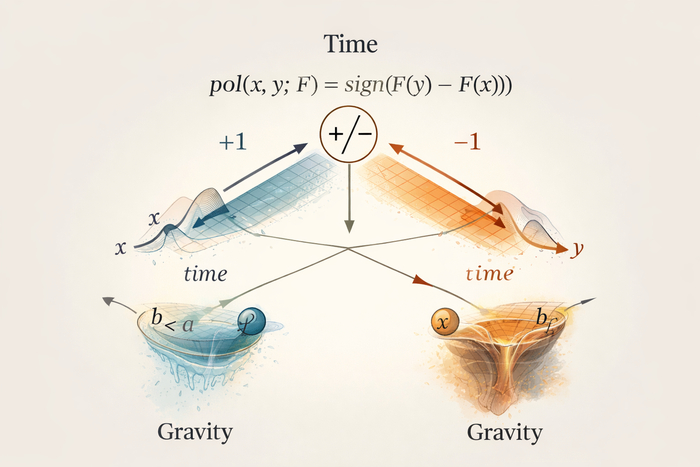
В бытовом языке полярность часто смешивают со «свойством объекта». В нашем подходе полярность относится не к вещи, а к переходу между двумя состояниями (или двумя вершинами графа). Она фиксирует направление относительно выбранной шкалы.

Пусть задана шкала F(x) (в дальнейшем роль такой шкалы будет играть потенциал). Тогда полярность перехода a → b определяется так:

pol(a,b;F) = sign(F(b) − F(a)) ∈ {+1, −1}.

Смысл:

• +1 означает «переход в сторону увеличения F»,

• −1 означает «переход в сторону уменьшения F».

Это не «заряд» и не «атрибут тела». Это минимальная операция ориентации: сравнить две величины и зафиксировать знак разности.

3. Геометрия без “пространства как сущности”: граф как носитель связности

Классическая механика привычно опирается на непрерывное пространство и метрику. В двухполярной гравитации допускается иной фундамент: граф.

• Вершины графа — состояния/точки учёта.

• Рёбра — допустимые переходы (связность).

• Вес ребра — мера «стоимости» или «близости» (в простейшем приближении связанная с расстоянием).

Важно: графовая геометрия не отрицает непрерывные модели. Она задаёт общий язык, в котором непрерывный предел получается как частный случай (например, при сгущении регулярной сетки).

4. Потенциал как центральная величина L2-канала

Двухполярная гравитация фиксирует следующий выбор: первичной величиной является потенциал Φ.

• В системе СИ Φ удобно мыслить в единицах м²/с².

• Движение «вниз» по потенциалу является определяющим смыслом тяготения.

В непрерывной форме ускорение задаётся стандартным соотношением:

a = −grad(Φ).

В графовой форме вместо grad используется дискретный аналог, но смысл сохраняется: ускорение направлено против роста потенциала.

5. Уравнение поля и роль оператора L

Поле порождается распределением источника, которое мы обозначим как ρ_g (гравитационная плотность, в СИ — кг/м³). Тогда основная форма уравнения поля записывается как:

L(Φ) = κ_B * ρ_g.

Здесь:

• L — оператор типа лапласиана (в непрерывном случае — обычный лапласиан; в графовом — лапласиан графа),

• κ_B — коэффициент моста режима B в выбранной нормировке.

В непрерывном ньютоновском пределе эта запись соответствует форме уравнения Пуассона, но мы сознательно оставляем её в виде «оператор L + источник», чтобы один язык охватывал и непрерывные, и графовые реализации.

6. Мост в СИ: κ_B как калибровка, а не “открытие”

Ключевое методологическое ограничение следующее: κ_B в режиме B — это калибровка моста к СИ, а не «величина, выведенная из аксиом природы».

В канонической нормировке режима B принимается:

κ_B = 4πG, и β = 1,

где G — гравитационная постоянная в СИ. Это не утверждение «мы вывели G». Это договор о том, как наша нормировка соотносится с общеупотребительным СИ-языком.

Именно поэтому любые разговоры о “новой константе” здесь методологически запрещены: двухполярная гравитация в этой версии не конкурирует с измерениями G, а использует их как внешний эталон моста.

7. Границы режима: запрет смешения L2 и многополярностей

Двухполярная гравитация в данной статье рассматривается как L2-канал. Это означает:

• никаких «зарядов» и многополярных степеней свободы внутри L2;

• никакого перехода к трёхполярности “по смыслу” без явного объявления нового режима и новых постулатов;

• все утверждения о поле и потенциале относятся к L2 и проверяются в L2.

Это ограничение не уменьшает теорию; оно делает её строгой. Любое расширение возможно, но только как отдельная ветвь с отдельными контрактами и проверками.

8. Принцип воспроизводимости как часть теории, а не “техническая деталь”

В классических изложениях воспроизводимость часто считается внешней по отношению к теории. Здесь она встроена в определение корректности:

• формулы задают вычисляемый объект,

• вычисление подтверждается эталонными задачами (точечные массы, оболочка, однородный шар, суперпозиция),

• любые изменения в операторе L, метрике или нормировке должны быть явными и проверяемыми.

Иначе говоря, теория в нашем смысле — это не только «что написано», но и «что стабильно воспроизводится».

Глава 2. Графовый оператор поля: лапласиан, дискретный градиент и непрерывный предел

1. Зачем графовый оператор нужен именно здесь

Если двухполярность понимать как механизм ориентации “вверх/вниз” по шкале, то потенциал Φ задаёт направление движения, а геометрия отвечает на вопрос: как сравнивать соседние состояния и как распространяется влияние источника.

В непрерывной механике эту роль играют:

• градиент (grad) — локальная направленность,

• лапласиан (Δ) — оператор, связывающий потенциал и источник.

В графовой геометрии эти же роли выполняют дискретные аналоги. Преимущество графа в том, что он:

• естественно описывает дискретные среды, сетки, структуры;

• допускает непрерывный предел как частный случай;

• позволяет явно фиксировать “метрику” через веса рёбер, не пряча её в координатах.

2. Граф, веса и смысл “дистанции”

Пусть задан связный неориентированный граф G = (V,E), где:

• V — множество вершин,

• E — множество рёбер.

Каждому ребру (i,j) назначим неотрицательный вес w_ij > 0. Вес фиксирует интенсивность связи: чем “ближе” вершины, тем обычно больше вес. В простейшем метрическом приближении берут:

w_ij = 1 / d_ij^2,

где d_ij — заданная длина (или стоимость) ребра. Это согласуется с интуицией ньютоновского ближнего влияния и хорошо ведёт себя на регулярных сетках.

Важно: вес — это место, где живёт геометрия. Если вы меняете w_ij, вы меняете геометрию взаимодействия. Поэтому в строгом режиме любые изменения весов должны быть явными и проходить тесты.

3. Лапласиан графа L и его “положительность”

Определим матрицу смежности с весами W и диагональную матрицу степеней D:

D_ii = сумма по j соседям i от w_ij.

Тогда ненормированный лапласиан графа:

L = D − W.

Для функции (поля) Φ на вершинах (то есть Φ_i = Φ(i)) дискретный лапласиан в вершине i записывается так:

(LΦ)_i = сумма по соседям j от w_ij * (Φ_i − Φ_j).

Смысл:

• если Φ_i больше средних соседей, (LΦ)_i положителен;

• если Φ_i меньше, (LΦ)_i отрицателен;

• оператор “штрафует” резкие перепады и тянет к гладкости.

Ключевое свойство: при w_ij > 0 лапласиан является положительным полуопределённым оператором. Это то, что обеспечивает корректность задачи поля и отсутствие “самопроизвольной антигравитации” при положительных источниках в статике.

4. Уравнение поля на графе (режим B)

На графе уравнение поля в режиме B имеет вид:

LΦ = κ_B * ρ_g.

Здесь ρ_g — дискретная плотность на вершинах (или на ячейках, сведённых к вершинам). Важно правильно согласовать размерности:

• Φ в СИ: м²/с²,

• ρ_g в СИ: кг/м³,

• L должен иметь размерность 1/м² (на регулярной сетке это достигается выбором d_ij как длины ребра и w_ij = 1/d_ij^2),

• тогда κ_B имеет размерность м³/(кг*с²), что согласуется с κ_B = 4πG.

Это один из ключевых моментов: графовая дискретизация не должна “случайно” менять размерности. Воспроизводимый режим требует, чтобы размерность была прозрачна и проверялась гейтом.

5. Граничные условия и “нуль потенциала”

В непрерывной задаче Пуассона решение без граничных условий неоднозначно (потенциал определён с точностью до константы). На графе ситуация аналогична: если граф “замкнут”, L имеет нулевое собственное значение, и Φ определено с точностью до добавления константы.

Строгое решение требует выбора одного из стандартных вариантов:

1. Зафиксировать потенциал на части границы (Dirichlet):
   Φ = 0 на boundary.

2. Зафиксировать среднее значение потенциала:
   сумма Φ_i = 0.

3. Ввести “якорную” вершину:
   Φ(anchor) = 0.

Для воспроизводимости удобнее вариант Dirichlet на внешней границе домена (например, на границе регулярной сетки), потому что тогда задача становится однозначной и хорошо тестируется на эталонах.

6. Дискретный градиент и ускорение на графе

В непрерывном виде ускорение:

a = −grad(Φ).

На графе существует несколько согласованных способов задать дискретный аналог. В минимальном варианте для ребра (i,j) вводят “перепад потенциала”:

ΔΦ_ij = Φ_j − Φ_i,

и рассматривают направленный вклад вдоль ребра, нормируя на длину ребра:

g_ij = (Φ_j − Φ_i) / d_ij.

Тогда “ускорение” в вершине i можно определить как сумму вкладов по соседям с ориентацией на убывание Φ. Простейшая конструкция:

a_i = сумма по соседям j от (w_ij * (Φ_j − Φ_i)) * e_ij,

где e_ij — единичный вектор направления от i к j (если граф вложен в пространство) или формальный базис ребра (если это абстрактный граф).

В задачах, где граф является регулярной 3D-сеткой, e_ij и d_ij естественно заданы, и a_i становится дискретным аналогом −grad(Φ).

Смысл двухполярности здесь прямой: знак (Φ_j − Φ_i) задаёт “полярность” перехода, а направление ускорения выбирается против роста Φ.

7. Непрерывный предел: как граф “сходится” к классике

Чтобы графовая теория была не произвольной игрушкой, она должна иметь непрерывный предел. Это достигается так:

• берём регулярную сетку с шагом h,

• соединяем соседей по 6 направлениям (в 3D),

• задаём d_ij = h,

• задаём w_ij = 1/h^2.

Тогда лапласиан графа аппроксимирует непрерывный лапласиан:

(LΦ)_i приближается к (−ΔΦ)(x_i) (с точностью до конвенции знака),

а уравнение

LΦ = κ_B * ρ_g

становится дискретизацией классического уравнения Пуассона.

Проверяемый факт: если вы берёте сферическую оболочку или однородный шар в виде дискретного распределения ρ_g на сетке, то при уменьшении шага h:

• поле вне шара стремится к полю точечной массы,

• внутри оболочки ускорение стремится к нулю,

• внутри шара ускорение стремится к линейной зависимости от радиуса.

Именно эти утверждения и являются “контрольными эталонами” непрерывного предела.

8. Почему это не “просто численный метод”

Можно сказать: “это всего лишь численное решение Пуассона”. Формально — да, если вы ограничитесь ньютоновским пределом. Но для двухполярной гравитации важно другое:

• графовая геометрия делает явным то, что в континууме скрыто в выборе координат и метрики;

• оператор L и веса w_ij становятся предметом теории, а не “деталью реализации”;

• благодаря контрактам и тестам вы получаете режим, который нельзя незаметно подменить, сохранив красивую риторику.

В этом и состоит методологическая ценность: теория не сводится к формуле, она включает дисциплину режима и воспроизводимость.

Глава 3. Мост в СИ: κ_B как калибровка, контуры воспроизводимости и гейты режима

1. Почему “мост” необходим и почему он не должен притворяться “открытием”

Любая теория поля, претендующая на сопоставимость с измерениями, обязана сказать, как её величины выражаются в системе единиц, где работают приборы. В нашем случае это СИ.

Но есть принципиальная развилка:

• либо мы честно признаём, что масштаб в СИ задаётся калибровкой,

• либо начинаем рассказывать, что “константа природы выведена из аксиом”, что почти всегда означает подмену смысла и скрытую подгонку.

В двухполярной гравитации выбран первый путь: коэффициент κ_B является мостом нормировки, а не эмпирическим “открытием”.

2. Канонический выбор режима B в СИ

В режиме B (L2, двухполярность) принимается каноника:

• β = 1,

• κ_B = 4πG,

где G — гравитационная постоянная в СИ.

Это означает следующее:

1. Двухполярный канал задаёт форму уравнения поля:

LΦ = κ_B * ρ_g.

1. Привязка к СИ устанавливается через внешнее значение G (как эталон), после чего κ_B фиксируется.

2. Мы не обсуждаем “истинность” G — мы используем его как принятую опору для пересчёта в СИ.

Этот подход аккуратно разделяет “внутреннюю теорию” и “внешнюю шкалу”.

3. Статус κ_B: CALIBRATION_ONLY

Чтобы не возникало даже возможности риторической подмены, κ_B фиксируется с явным статусом:

• κ_B — CALIBRATION_ONLY.

Смысл этого статуса:

• κ_B не является выводом из аксиом,

• κ_B не является новым измерением,

• κ_B не является аргументом в споре с CODATA,

• κ_B — это согласование внутренней нормировки L2 с СИ.

Это жёсткое методологическое правило. Если кто-то начинает говорить “мы вывели κ_B из логики”, он выходит за рамки режима B и должен явно объявить другой режим и другую программу проверки.

4. Зачем нужен контур claims → валидатор → отчёт

Вопрос “как вы получили числа” обычно убивает большинство проектов на стадии презентации: либо неясно, откуда взято, либо можно подменить режим незаметно.

Поэтому в двухполярной гравитации воспроизводимость включена внутрь режима как обязательная часть. В простейшей форме контур выглядит так:

1. Источник (данные или документ) фиксируется контрактом:
   что извлечено,
   в каких единицах,
   с каким смыслом,
   какой режим,
   какие хеши файлов.

2. Анализатор формирует claims:
   утверждения в машинно-читаемом виде (например, “G = …, uncertainty = …, method = …”).

3. Валидатор проверяет:
   размерности,
   соответствие канонике (β=1, κ_B=4πG),
   отсутствие смешения L2 и L3,
   целостность файлов (хеши),
   отсутствие дублей и подмен.

4. Только после PASS допускается вычисление итоговых величин и выпуск отчёта.

Даже если в “мини”-режиме мы не строим “облако G”, сам принцип остаётся: любая цифра, попавшая в отчёт, обязана пройти валидатор.

5. Режимные гейты: зачем они и что именно запрещают

Гейт — это формализованный запрет на типовую подмену. Для нашего режима важны три класса гейтов.

5.1. Гейт размерностей

Проверяет, что:

• Φ имеет смысл потенциала (м²/с² в СИ),

• ρ_g имеет смысл плотности (кг/м³),

• оператор L имеет размерность 1/м² (при заданной геометрии/весах),

• κ_B имеет размерность м³/(кг*с²).

Если размерности не сходятся, то “теория” превращается в набор символов без физического содержания.

5.2. Гейт канона (β, κ_B)

Проверяет, что:

• β действительно равен 1 в режиме B,

• κ_B определён как 4πG_ref,

• G_ref — фиксированная внешняя опора,

• никакие “альтернативные конвенции” не подменяют канон молча.

Смена канона допускается только через явный запрос изменения (в проектной дисциплине — отдельный CHANGE_REQUEST), иначе это скрытая подгонка.

5.3. Гейт разделения L2 и L3

Проверяет, что:

• в L2-документах и расчётах нет L3-лексики, кроме нормативных дисклеймеров,

• κ_B не переносится в многополярные ветки как “универсальная константа”,

• любые многополярные эффекты не объявляются “следствием L2”.

Это предотвращает главный вид интеллектуальной коррупции: когда базовый рабочий канал начинает использоваться как риторический фундамент для более рискованных заявлений.

6. Что именно считается “результатом” в режиме B

После введения канона и гейтов результат в режиме B имеет чёткий статус:

• результатом является воспроизводимая процедура вычисления Φ и a из ρ_g и геометрии (графа или континуума),

• плюс согласованный мост в СИ через κ_B,

• плюс доказательство корректности на эталонных задачах.

Результатом не является:

• “новая физическая константа”,

• “антигравитация”,

• “объяснение всего”.

Этот список ограничений не обедняет модель, а фиксирует её честные границы применимости.

7. Почему именно такой стиль даёт устойчивость проекта

В истории науки многократно повторялся сюжет: сильная идея гибнет от слабого протокола. Здесь делается обратное:

• идея (двухполярность + граф) задаёт язык,

• протокол (claims/валидатор/гейты) защищает язык от деградации,

• тесты (эталоны и непрерывный предел) обеспечивают контроль качества.

В результате теория становится не “текстом, который можно пересказать”, а механизмом, который либо проходит проверку, либо ломается.

Глава 4. Эталонные проверки: что именно мы обязаны воспроизводить и почему

1. Зачем вообще нужны эталоны

Теория поля без набора эталонных проверок быстро превращается в повествование: формулы есть, но неизвестно, что именно они означают и не “сломаны” ли они незаметно. В двухполярной гравитации эталоны играют роль минимального фильтра зрелости:

• они фиксируют смысл Φ и a,

• они связывают графовую реализацию с непрерывным пределом,

• они обнаруживают подмены нормировок, знаков, граничных условий и метрик.

Важно: эталонные проверки в нашем режиме — не “иллюстрации”, а обязательный тестовый набор, который должен проходить при каждом существенном изменении оператора L, весов w_ij, постановки граничных условий или расчётного пайплайна.

2. Базовый эталон №1: точечная масса

Самый простой случай — одна точечная масса M и точка наблюдения на расстоянии r.

Классический потенциал:

Φ(r) = − G*M / r.

Ускорение (по модулю):

|a(r)| = G*M / r^2,

направление — к источнику.

Почему это важно:

• задаёт знак потенциала и направление “вниз по Φ”;

• сразу выявляет ошибки знака в a = −grad(Φ);

• даёт контроль масштабирования и размерностей.

В дискретном (графовом) виде точечная масса реализуется как концентрированный источник ρ_g в одной вершине (или небольшой окрестности) и проверяется зависимость поля от расстояния (в непрерывном пределе — 1/r и 1/r^2).

3. Базовый эталон №2: сферическая оболочка

Сферическая оболочка (тонкий слой массы на радиусе R) — один из самых строгих и удобных эталонов. В классике верны два утверждения:

1. Внутри оболочки (r < R) ускорение равно нулю:

a(r) = 0.

Потенциал внутри постоянен:

Φ_inside = − G*M / R.

1. Снаружи оболочки (r > R) поле эквивалентно полю точечной массы в центре:

Φ(r) = − GM / r,
|a(r)| = GM / r^2.

Почему это важно:

• это тест “правильной глобальности” решения: оболочка создаёт поле вне, но не создаёт ускорение внутри;

• в дискретизации оболочка чувствительна к ошибкам геометрии и к граничным условиям;

• для графового лапласиана это ключ к проверке континуального предела: на грубой сетке возможны остаточные ошибки внутри, но при сгущении сетки они обязаны убывать.

Если ваш графовый солвер выдаёт заметное ускорение внутри оболочки и эта ошибка не уменьшается при улучшении дискретизации — значит, либо неверна постановка, либо нарушены свойства оператора L.

4. Базовый эталон №3: однородный шар

Для однородного шара радиуса R и массы M классическая теория даёт:

1. Снаружи (r > R) как точечная масса:

Φ(r) = − GM / r,
|a(r)| = GM / r^2.

1. Внутри (r < R) ускорение линейно по радиусу:

|a(r)| = GMr / R^3.

Потенциал внутри выражается квадратично по r (важен не вид, а согласованность со связью a = −dΦ/dr).

Почему это важно:

• проверяет, что ваша схема правильно воспроизводит “внутреннее поле” распределённой массы;

• даёт тест на корректность обработки ρ_g как объёмной плотности;

• выявляет ошибочные “эффекты оболочки” внутри шара (когда дискретизация фактически превращает шар в оболочку).

В контуре L2 этот эталон особенно важен, потому что он показывает: теория работает не только для “суммы точек”, но и для распределённых источников.

5. Базовый эталон №4: суперпозиция и инвариантность к перестановке

Линейность уравнения Пуассона в режиме B означает суперпозицию:

если ρ_g = ρ_1 + ρ_2, то Φ = Φ_1 + Φ_2.

Это приводит к двум проверкам:

1. Суперпозиция нескольких точечных источников должна равняться сумме отдельных решений (в пределах численной погрешности).

2. Перестановка источников (и порядок суммирования вкладов) не должна менять результат. Любая зависимость от порядка — признак вычислительного дефекта (или скрытой нелинейности, которая в режиме B не допускается).

Почему это важно:

• защищает от тонких ошибок реализации (особенно в численном решателе и при обработке источников);

• дисциплинирует переход к более сложным конфигурациям.

6. Численная дискретизация распределённых масс: что считается допустимой ошибкой

Когда шар или оболочка реализуются на сетке, возникают два класса ошибок:

• дискретизационная (приближение геометрии и оператора),

• решательская (точность решения линейной системы).

Корректная теория должна предъявлять не “магическое совпадение”, а ясную картину:

• внутри оболочки ускорение должно стремиться к нулю при уточнении сетки;

• для шара внутренняя линейность ускорения должна улучшаться при уточнении;

• вне тела поле должно сходиться к 1/r^2.

Важный практический принцип: ошибка допустима, если она:

• мала,

• имеет понятную причину (сеточный шаг, граничные условия),

• монотонно уменьшается при улучшении дискретизации.

Если ошибка “скачет” или растёт — это не физика, а дефект постановки.

7. Континуальный предел графового лапласиана: проверка зрелости графовой реализации

Графовый оператор L и выбранные веса w_ij должны вести к классике при сгущении сетки. Проверка “континуального предела” означает:

• берём регулярную 3D-сетку с шагом h,

• задаём w_ij = 1/h^2 и корректные граничные условия,

• формируем дискретную ρ_g (шар/оболочка),

• решаем LΦ = κ_B*ρ_g,

• сравниваем с аналитическими формулами.

Критерий зрелости: при уменьшении h графовая реализация приближается к непрерывной.

Это принципиально отличает теорию от “произвольного графового эффекта”. Если нет континуального предела, то граф перестаёт быть геометрическим описанием и становится произвольной машиной.

8. Почему набор эталонов минимален и достаточен

Перечисленные эталоны — не случайный список. Они закрывают четыре независимых класса свойств:

• знак и масштаб поля (точечная масса),

• глобальная согласованность и симметрия (оболочка),

• объёмная плотность и внутреннее поле (шар),

• линейность и устойчивость вычислений (суперпозиция).

Если теория проходит эти проверки, она становится пригодной как база для дальнейших вычислений, расширений и обсуждений. Если не проходит — разговор о “готовой теории” преждевременен.

Глава 5. Итоги, границы применимости и направления развития

1. Что в итоге построено

Двухполярная гравитация в изложенном режиме (L2, Mode B, СИ) представляет собой минимальную, но завершённую конструкцию, состоящую из четырёх взаимосвязанных частей.

1. Онтология канала:
   первична величина потенциала Φ; движение определяется ориентацией по потенциалу; полярность — знак перехода относительно шкалы.

2. Геометрия:
   средой для вывода может быть как непрерывное пространство, так и граф. В графовой версии геометрия задаётся связностью и весами рёбер.

3. Уравнение поля:
   поле задаётся уравнением вида
   LΦ = κ_B * ρ_g,
   а ускорение — правилом
   a = −grad(Φ)
   (или дискретным аналогом).

4. Воспроизводимость как часть корректности:
   теория не считается “собранной”, пока она не проходит эталонные тесты (точечная масса, оболочка, шар, суперпозиция, континуальный предел графа) и пока не защищена гейтами режима.

Эта сборка даёт не “картину мира”, а устойчивый расчётный канал: если заданы ρ_g и геометрия, можно вычислять Φ и a.

2. Главный методологический тезис: κ_B — это калибровка, а не открытие

Коэффициент κ_B в режиме B фиксируется как мост нормировки к СИ:

κ_B = 4πG, при β = 1.

Это означает:

• κ_B не является выводом из аксиом природы;

• κ_B не является новой оценкой G;

• κ_B — согласование масштаба поля в СИ.

Именно это удерживает теорию в строгих границах: её сила — в форме, воспроизводимости и проверяемости, а не в претензии “мы пересчитали мир”.

3. Границы применимости: что можно и чего нельзя утверждать

3.1. Что можно утверждать публично

• В режиме L2/Mode B построен воспроизводимый расчёт потенциала и ускорения для заданной плотности ρ_g и заданной геометрии (континуальной или графовой).

• Графовый оператор L канонизирован так, что при сгущении сетки даёт непрерывный ньютоновский предел.

• Корректность подтверждается эталонными проверками (оболочка, шар и др.) и автоматическими гейтами.

3.2. Чего утверждать нельзя (и почему)

• Нельзя утверждать “антигравитацию” как следствие L2, потому что при положительной плотности и стандартном операторе L в статике получается ньютоновский тип притяжения.

• Нельзя утверждать “новую константу” или “вывод G”, потому что κ_B — калибровка моста.

• Нельзя смешивать L2 и многополярные режимы: любые L3-гипотезы требуют отдельного режима, отдельного контракта и отдельного тестового набора.

Эти запреты — не риторика, а защита от методологической деградации.

4. Почему графовая версия является принципиальной, а не декоративной

Графовая геометрия в этой конструкции выполняет роль “обнажителя” скрытых выборов:

• В континууме выбор метрики и дискретизации часто прячется в координатах и численных методах.

• В графе выбор геометрии вынесен наружу: в w_ij, в тип соседства, в граничные условия.

Это делает теорию удобной как инженерный инструмент и как исследовательский язык: любые изменения геометрии фиксируются явно и могут быть привязаны к тестам.

5. Какой тип предсказательности доступен в текущей версии

В “мини”-версии предсказательность имеет два уровня.

1. Физический ньютоновский уровень:
   при заданном распределении массы теория предсказывает поле и движение так же, как ньютоновская гравитация (в рамках её применимости). Это предсказательность корректного канала, а не новой физики.

2. Инженерный уровень качества:
   теория предсказывает, как будет меняться точность при уточнении сетки, как сойдётся графовая дискретизация, где возникнут ошибки и как они обязаны убывать. Это предсказательность воспроизводимости.

Если нужен третий уровень — “отличия от Ньютона” — требуется расширение режима, а значит отдельная программа проверки.

6. Два направления развития без разрушения дисциплины

6.1. Развитие A: универсальный солвер на графах

Это наиболее естественное продолжение в рамках L2:

• расширить типы графов (не только регулярные сетки);

• формализовать выбор весов для неевклидовых структур;

• ввести стандартизованные граничные условия для конечных доменов;

• добавить интегратор траекторий: источники → Φ → a → движение.

Результат: L2 становится универсальным вычислителем гравитационного потенциала на произвольной связности.

6.2. Развитие B: осторожные расширения за пределы режима B

Если появится мотивация строить “новую физику”, то корректный путь один:

• объявить новый режим (не L2/Mode B),

• ввести новый постулат (например, модификацию весов, нелинейность, новые степени свободы),

• построить отдельный тестовый набор, который отличает новый режим от ньютоновского,

• зафиксировать мосты и калибровки отдельно, без переноса κ_B “как универсального ключа”.

Это позволяет расширять модель, не разрушая надёжное ядро.

7. Итоговая формула: что означает “готова теория” в нашем смысле

В нашем подходе “теория готова” означает:

• определения зафиксированы так, что их нельзя интерпретировать произвольно;

• вычислимые величины существуют и однозначно считаются;

• связь с СИ оформлена как калибровка, а не как мифологема;

• режим защищён гейтами от подмен и смешений;

• минимальный набор эталонов проходит автоматически.

В этом смысле двухполярная гравитация как L2/Mode B является не обещанием, а работающей, проверяемой процедурой.

Глава 6. Заключение: время в L2 как порядок фиксаций, чистота режима и границы релятивистских сюжетов (от первого лица)

1. Почему я считаю L2 изящной теорией

Я называю двухполярную гравитацию (L2, режим B) изящной не потому, что она “объясняет всё”, а потому, что она строго отделяет определённое от недоопределённого. Я фиксирую минимальный набор конструкций, из которых действительно можно воспроизводимо построить гравитационное описание:

• двухполярность как знак разности по выбранной шкале;

• графовую (или континуальную) геометрию как носитель связности;

• потенциал Φ как центральную шкалу гравитационного канала;

• источник ρ_g и оператор L как механизм построения Φ;

• и — что принципиально — время L2, которое в моём режиме не исчезает, но имеет строго определённый статус.

Эта “минимальность” — не упрощение, а дисциплина: в L2 нельзя тайком подмешивать световые инварианты и собственное время, потому что тогда я разрушу смысл самого режима.

Вся матрица мышления и теория доступна в ChatGPT

Просто вставьте в новый чат архив

# Текст для вставки в новый чат: следуй инструкциям в файле

DOCS/NEW_CHAT_PROMPT_iter372.md

Читать далее:

Двухполярная гравитация: что это такое, если базис — только «+ / »

Как из двухполярности естественно получается «энтропийная стрела времени» и почему превращение шкалы в сущность рождает ложные парадоксы

Что такое время в двухполярной (обыденной) модели и почему это определение выигрывает у «метафизических» теорий

Природа времени и гравитации. Простая и ясная теория

Троица в христианстве: как L3-логика снимает видимость противоречий

Что такое разум с позиции L3-логики, или как «Алмазная сутра» учит нас разуму

Ноль и единица в трёхполярной логике: почему бинарность недостаточна и как работает трёхполярный гиперграф

Трёхполярный гиперграф L3 v0.1.0: нелинейная многополярная система, которая объясняет всё — от ИИ до солнечных циклов

2) Геометрия без пространства: граф как носитель расстояний

Вместо непрерывного пространства вводится граф:

G = (V, E),

где:

• (V) — узлы (регионы, ячейки, состояния места),

• (E) — связи соседства.

На каждом ребре ((u,v)) задано расстояние:

d(u,v) > 0.

Из расстояния задаётся «проводимость» (канонически):

w(u,v) = 1 / d(u,v)^2.

Это чисто геометрическая нормировка: ближние связи сильнее дальних.

3) Источник гравитации без зарядов: ρ_g как плотность невыполненных ограничений

В двухполярной версии, которая выбрана канонической, источник — не «вещество» и не заряд, а структурная невыполненность.

В каждом узле (u) задан набор ограничений (C(u)).
У каждого ограничения (c) есть вес (\alpha(c) > 0).
И есть булева проверка:

sat(c,u,S) ∈ {0,1}.

Тогда:

ρ_g(u) = Σ_{c ∈ C(u)} α(c) * (1 − sat(c,u,S)).

Свойства:

• ρ_g(u) ≥ 0 всегда.

• Знака нет, отрицательных значений нет.

• Следовательно, «отталкивание по знаку» в этой модели не появляется: гравитация однонаправленна.

4) Потенциал Φ: как получить «скалярное поле» строго из L2

Определяем оператор дискретного лапласиана на графе.

Матрица проводимостей:
W_uv = w(u,v) если (u,v) ∈ E, иначе 0.

Диагональная матрица степеней:
D_uu = Σ_v W_uv.

Лапласиан:
L = D − W.

Потенциал Φ: V → R задаётся уравнением Пуассона на графе:

L Φ = κ ρ_g,

где κ > 0 — коэффициент нормировки (калибровка шкал), а не «заряд» и не «энергия».

Калибровка (обязательна)

Поскольку Φ определена с точностью до добавления константы, нужно выбрать калибровку:

вариант А: Φ(u0) = 0,
или вариант Б: Σ_u Φ(u) = 0.

Без этого утверждение «Φ найден» считается недействительным.

5) Гравитация как функция разности: «вниз по Φ»

На ребре (u,v) вводится уклон:

g(u→v) = − (Φ(v) − Φ(u)) / d(u,v).

И двухполярная ориентация ребра по потенциалу:

pol(u,v;Φ) = sign(Φ(v) − Φ(u)).

Тогда «падение» — это выбор перехода с отрицательной разностью потенциала:

двигаться u→v предпочтительно, если Φ(v) < Φ(u),
то есть pol(u,v;Φ) = −1.

Это и есть двухполярная гравитация в чистом виде: не субстанция, не поле-вещество, а ориентация и уклон.

6) Динамика без сущностного времени: порядок шагов

В L2-времени «время» — это порядок шагов (n = 0,1,2,\dots). Если нужна числовая координатизация шага, вводится dt как масштаб.

Самый минимальный алгоритм движения (градиентный спуск по Φ):

u_{n+1} = argmin_{v: (u_n,v)∈E} Φ(v).

Если вы хотите инерцию, вводится скорость, но это уже надстройка:

v_{n+1} = v_n + a(u_n) * dt,
x_{n+1} = x_n + v_n * dt.

Где (a(u)) вычисляется из локального “градиента” Φ (на графе — из разностей по соседям).

7) В чём смысл и отличие от «обычной» гравитации

7.1. Здесь нет «массы как сущности», но есть источник

Источник — ρ_g, и он выражает не «количество вещества», а количество структурно невыполненных требований.

Если считать, чтобы «масса» возникает как измеряемый параметр, она будет производной агрегатной меры ρ_g по региону:

M_eff(region) = Σ_{u∈region} ρ_g(u) * vol(u)

(где vol(u) — вес ячейки; если нет объёмов, можно брать 1).

7.2. Нет зарядов и нет знаковых источников

Это фундаментально: ρ_g ≥ 0. Поэтому гравитация однонаправленна и не требует обсуждать «антигравитацию по отрицательному заряду».

7.3. Нет энергии как первичного объекта

Φ вводится не как «энергия», а как решение уравнения на графе. Это устраняет типичные ложные парадоксы реификации.

8) Почему это всё именно «двухполярность»

Потому что единственный “онтологический” механизм направления здесь — знак разности:

pol = sign(ΔΦ) ∈ {+1, −1}.

И именно этот знак задаёт стрелку движения. Всё остальное — геометрическая инфраструктура: граф, расстояния, лапласиан, калибровка.

9) Короткая каноническая формула

Двухполярная гравитация — это ориентация по убыванию потенциала Φ на графе. Источник задаётся как плотность невыполненных ограничений: ρ_g(u)=Σ α(c)(1−sat). Потенциал Φ определяется уравнением LΦ=κρ_g при обязательной калибровке. Поле на ребре — уклон g(u→v)=−(Φ(v)−Φ(u))/d(u,v), а направление задаётся знаком pol=sign(Φ(v)−Φ(u)). Гравитация здесь — функция и правило движения, а не вещество и не заряд.

Как в L2 получить ньютоновское 1/r^2: простое изложение с простыми формулами

Ниже я переписываю тот же смысл максимально «на пальцах», но формулы оставляю, просто в самом прямом виде. Всё это — строго двухполярность (L2).

1) Что такое двухполярная гравитация в одной строке

Есть потенциал Φ на узлах графа.

Гравитация — это правило: двигайся туда, где Φ меньше.

Знак (двухполярность) задаётся так:

pol(u→v) = sign( Φ(v) − Φ(u) )

Если Φ(v) < Φ(u), то Φ(v) − Φ(u) < 0, значит pol = −.

Это и есть «падение».

2) Геометрия: граф и расстояния

Есть граф G=(V,E).

У каждого ребра (u,v) есть расстояние:

d(u,v) > 0

Для вычислений берём вес ребра:

w(u,v) = 1 / d(u,v)^2

(это просто “ближе = сильнее связь”).

3) Источник: ρ_g как «сколько ограничений не выполнено»

В каждом узле u есть список ограничений C(u).

У каждого ограничения c есть вес α(c) > 0.

И есть проверка:

sat(c,u,S) = 1 (выполнено)

sat(c,u,S) = 0 (не выполнено)

Тогда источник:

ρ_g(u) = Σ_{c∈C(u)} α(c) * (1 − sat(c,u,S))

Если ограничение выполнено, (1−sat)=0 и оно не даёт вклад.

Если не выполнено, (1−sat)=1 и вклад равен α(c).

Важно:

ρ_g(u) ≥ 0 всегда.

Знака нет. “Отталкивания по минусу” не появится.

4) Как получить Φ из ρ_g (главная формула)

Сначала вводим “лапласиан” на графе.

Для каждого узла u:

Deg(u) = Σ_{v сосед u} w(u,v)

Тогда уравнение для Φ в узле u:

Deg(u)*Φ(u) − Σ_{v сосед u} w(u,v)*Φ(v) = κ * ρ_g(u)

Это и есть запись LΦ = κρ_g, только в «ручном» виде.

Где κ>0 — коэффициент масштаба (калибровка).

Он не “заряд” и не “энергия”, просто нормировка шкал.

5) Калибровка Φ (обязательно)

Φ можно сдвигать на константу, и разности не изменятся.

Поэтому фиксируем ноль:

Φ(u0) = 0

или

Σ_u Φ(u) = 0

Без этого решение не считается завершённым.

6) “Ускорение” или “сила” на ребре (простая формула)

На ребре (u,v) считаем уклон:

g(u→v) = −(Φ(v) − Φ(u)) / d(u,v)

Если Φ(v) меньше, чем Φ(u), тогда (Φ(v)−Φ(u)) отрицательно,

минус перед скобкой делает g положительным “в сторону v”.

То есть система тянется вниз по Φ.

7) Почему в 3D получается 1/r^2 (без мистики)

Ключевой принцип: “поток сохраняется”.

Есть область Ω (например, “шар” радиуса r вокруг источника).

Сумма источника внутри:

M_eff(Ω) = Σ_{u∈Ω} ρ_g(u)

Тогда поток через границу примерно постоянен:

Flux(∂Ω) = κ * M_eff(Ω)

Это дискретный аналог “теоремы Гаусса”.

Дальше простая геометрия:

в 3D “площадь границы шара” растёт как

Area(∂Ω(r)) ~ 4π r^2

Если общий поток постоянный, а площадь растёт как r^2,

то “средняя сила на единицу площади” убывает как 1/r^2.

Отсюда:

|grad Φ|(r) ~ (κ * M_eff) / (4π r^2)

А гравитация — это как раз “вниз по Φ”, то есть:

|g(r)| ~ (κ * M_eff) / (4π r^2)

Это и есть ньютоновская форма: 1/r^2.

8) Как выбирать ограничения C(u), чтобы источник был «точечным»

Чтобы было “как масса”, нужно:

• вне объекта: ρ_g(u)=0

• внутри объекта: ρ_g(u) > 0

То есть:

если u не в объекте O → C(u)=∅ → ρ_g(u)=0

если u в объекте O → задаём несколько ограничений c и делаем их невыполненными → sat=0 → ρ_g растёт.

Тогда суммарная “масса” объекта:

M_eff = Σ_{u∈O} ρ_g(u)

9) Когда 1/r^2 не получится (и это нормально)

1/r^2 получается, только если:

• граф на больших масштабах ведёт себя как 3D (граница ~ r^2),

• источник локален (ρ_g сосредоточена),

• веса w и лапласиан согласованы с расстояниями.

Если граф “плоский” (2D), будет не 1/r^2.

Если граф “сверхсвязный”, спад будет другой.

Это не ошибка — это диагностика геометрии.

Короткий итог (в 6 строк)

Источник:

ρ_g(u) = Σ α(c) * (1 − sat)

Уравнение потенциала в узле u:

Deg(u)*Φ(u) − Σ w(u,v)*Φ(v) = κ ρ_g(u)

Вес ребра:

w(u,v)=1/d(u,v)^2

Гравитация на ребре:

g(u→v)=−(Φ(v)−Φ(u))/d(u,v)

Направление падения:

идём туда, где Φ меньше

Ньютоновский предел в 3D:

|g(r)| ~ (κ M_eff)/(4π r^2)

Если есть вопросы, просто загрузите архив и вставьте в чат ChatGPT. Далее достаточно написать: «Архив во вложении. Старт: следуй NAVIGATOR_NEXTCHAT_NETWORK_THINKING_iter355.md »

Читать далее:

Как из двухполярности естественно получается «энтропийная стрела времени» и почему превращение шкалы в сущность рождает ложные парадоксы

Что такое время в двухполярной (обыденной) модели и почему это определение выигрывает у «метафизических» теорий

Природа времени и гравитации. Простая и ясная теория

Троица в христианстве: как L3-логика снимает видимость противоречий

Что такое разум с позиции L3-логики, или как «Алмазная сутра» учит нас разуму

Ноль и единица в трёхполярной логике: почему бинарность недостаточна и как работает трёхполярный гиперграф

Трёхполярный гиперграф L3 v0.1.0: нелинейная многополярная система, которая объясняет всё — от ИИ до солнечных циклов

то получаю двухполярное время как частичный или линейный порядок на множестве состояний. Числа (F) при этом вторичны: они просто удобный способ стабилизировать сравнения.

Дальше важен выбор (F). Если я выбираю (F = t), я получаю «часы». Если я выбираю (F = \Phi), получаю «вверх/вниз по потенциалу». Если я выбираю (F = S), получаю «энтропийную стрелу».

2) Энтропия как частный случай шкалы F

Пусть система имеет множество микросостояний (\Omega), а то, что мы в опыте называем «состоянием», часто является макросостоянием (M), то есть классом микросостояний, неразличимых на уровне наблюдения.

Классическая формула Больцмана:

S(M) = k * ln W(M),

где (W(M)) — число микросостояний (кратность) внутри макросостояния (M), а (k) — постоянная Больцмана.

Вот здесь и появляется точное совпадение с моей двухполярной схемой. Беру

F = S.

Тогда двухполярный знак на паре макросостояний:

pol(M1, M2; S) = sign(S(M2) − S(M1)).

И «энтропийная стрела времени» в самой строгой форме — это правило ориентации:

M1 <_S M2 ⇔ S(M1) < S(M2).

То есть «вперёд» по энтропийной стреле означает «в сторону большего числа совместимых микросостояний».

На пальцах: система почти всегда “перетекает” туда, где вариантов больше.

3) Почему эта стрела «естественна»: вероятностная причина в двухполярном виде

Ключевой факт статистической физики можно выразить без сложной физики, просто через кратности.

Если я ничего «волшебного» не делаю, а только допускаю случайную эволюцию микросостояния, то вероятность попасть в макросостояние пропорциональна числу микросостояний в нём:

P(M) ∝ W(M).

А значит, если есть два макросостояния M_low и M_high, такие что

W(M_high) >> W(M_low),

то “типичная” траектория почти неизбежно чаще будет попадать в M_high.

Перепишем через энтропию:

W(M_high) >> W(M_low) ⇔ ln W(M_high) >> ln W(M_low) ⇔ S(M_high) >> S(M_low).

И вот уже готова «двухполярная причинность» энтропийной стрелы:

если S растёт, то “направление типичных переходов” совпадает с полярностью “+” по шкале S.

Можно даже написать «локальное правило шага» как у нас для гравитации, только без геометрии:

M_{n+1} выбирается так, чтобы S(M_{n+1}) − S(M_n) было, как правило, ≥ 0.

Это не абсолютный закон (флуктуации возможны), но это устойчивое правило направленности. В двухполярном языке:

ожидаемое значение E[ pol(M_n, M_{n+1}; S) ] положительно.

4) Как энтропийная стрела становится «временем» (и в каком смысле)

Теперь я связываю это с нашим определением времени как порядка.

Двухполярное время — это (E,<). Здесь вместо событий можно взять «состояния на шагах протокола» или «макросостояния системы». Тогда:

время по энтропии = порядок <_S, заданный шкалой S.

Это означает, что «прошлое/будущее» в энтропийной стрелке определяется относительно выбранного now (опорного состояния):

Past(now) = { M | S(M) < S(now) } Future(now) = { M | S(M) > S(now) }.

И важное: это не “второе время”, не «сущность времени», а частный способ упорядочить состояния по шкале.

5) Почему попытка сделать шкалу сущностью рождает ложные парадоксы

Вот тонкое место. Энтропия как шкала (F) — это функция, зависящая от уровня описания. Она определена на макросостояниях, а макросостояния зависят от того, какие различения мы считаем существенными.

Если я превращаю шкалу в сущность, я совершаю типичную ошибку: реификацию.

5.1. Парадокс «энтропия всегда должна расти» (как логическая ошибка)

Если считать S сущностью-двигателем, возникает ложное требование:

S всегда строго растёт на любой траектории.

Но в реальности:

• есть флуктуации;

• есть локальные уменьшения энтропии;

• есть системы с внешним потоком энергии, где локальная «энтропия подсистемы» может уменьшаться при росте энтропии окружения.

Парадокс появляется не потому, что физика противоречива, а потому что «шкалу типичности» сделали «онтологическим законом без условий».

В двухполярной грамотной форме правильно так:

S — это F, по которому мы ориентируем типичное направление в данном режиме и при данных границах системы.

5.2. Парадокс «время = энтропия» (смешение типов)

Когда шкалу превращают в сущность, появляется ещё более грубая подмена:

“время и есть энтропия”.

Но время в нашей двухполярной логике — это структура порядка (E,<), а энтропия — один из возможных (F), задающих ориентацию в частном классе систем и режимов описания.

То есть корректно:

энтропийная стрела задаёт частичный порядок <_S на состояниях,

а некорректно:

S является временем как сущностью.

Отсюда рождаются типичные псевдоспоры: «а как же системы с убывающей энтропией — там время назад?» Это не физический парадокс, это следствие подмены «ориентации по шкале» на «тождество сущности».

5.3. Парадокс «а почему прошлое не такое же вероятное, как будущее»

Шкала S объясняет асимметрию типичных траекторий при условии, что стартовое состояние было низкоэнтропийным. Но если сделать S сущностью, хочется «доказать», что S сама принуждает мир начинаться с низкой энтропии. Это классическая ловушка: пытаются извлечь из шкалы не только направление, но и начальные условия.

В корректной форме:

S задаёт вероятностную направленность переходов, но не обязана порождать низкоэнтропийный старт.

Если сделать шкалу сущностью, возникает псевдо-парадокс: «энтропия говорит, что всё должно быть высокоэнтропийно всегда, но мы видим низкоэнтропийные структуры». На деле это вопрос о граничных условиях и об открытых системах, а не «противоречие энтропии».

5.4. Парадокс «энтропия объективна как число, значит она независима от описания»

Ещё одна типичная реификация: считать, что S — абсолютная сущность, не зависящая от coarse-graining (уровня усреднения).

Но формула Больцмана прямо показывает зависимость от макроразбиения: (W(M)) определяется тем, какие микросостояния мы считаем «одним и тем же» макросостоянием. При другом разбиении другое (W), другая S.

Поэтому корректно:

S — объективна внутри выбранного режима описания (что считаем макросостоянием), но не обязана быть “абсолютной сущностью без режима”.

6) На пальцах: как держать всё правильно

Правильная картина:

• Есть система, есть множество микровариантов.

• Мы выбираем уровень описания (что считаем макросостоянием).

• Энтропия S — шкала, которая измеряет «сколько микровариантов соответствует этому макроописанию».

• Двухполярный знак “+ / −” по S даёт направление: “скорее туда, где вариантов больше”.

• Если вы делаете S сущностью, вы начинаете требовать от мира невозможное: абсолютного роста, независимости от режима, и объяснения начальных условий. Так рождаются ложные парадоксы.

7) Итог в формуле

Энтропийная стрела времени — это частный случай нашей общей двухполярной схемы:

F = S, pol(x,y;S) = sign(S(y) − S(x)), x <_S y ⇔ S(x) < S(y).

А ложные парадоксы возникают, когда делают запрещённый переход:

“F как шкала сравнения” -> “F как сущность мира”.

То есть когда функцию оценки начинают трактовать как самостоятельный объект, который «двигает» реальность, вместо того чтобы понимать её как инструмент упорядочивания и объяснения типичности в выбранном режиме.

Инженерная вставка: как хранить шкалу (F=S) в машинном контуре, отличать «энтропийную стрелу» от «клея» и гейтить фразу «энтропия есть время»

Ниже я описываю минимальный машинный слой так, чтобы энтропийная стрела времени была корректной проекцией (шкалой (F)), а попытка превратить шкалу в сущность автоматически давала BLOCK/FAIL с понятным диагнозом и рецептом переписывания.

1) Базовые типы: время как порядок, энтропия как шкала

В машинном контуре фиксируется типовая дисциплина.

Время (двухполярное) хранится как порядок на событиях/состояниях:

(T2 = (E,\ <)).

Шкала хранится как функция оценки:

(F: X \to R).

Энтропия — это конкретная шкала:

(F = S), где (S(M)=k\ln W(M)).

Энтропийная стрела — это ориентирование порядка через (S):

(x <_S y \Leftrightarrow S(x) < S(y)).

Критически важно для валидатора: “время” и “шкала” — разные типы сущностей в данных. Никаких «тождеств» между ними в одном типе предикации быть не должно.

2) Как представить шкалу, порядок и полярность в данных

Минимальная структура данных должна уметь выразить три вещи: шкала, сравнение, ориентация.

Шкала:

(F = \langle id,\ domain,\ codomain,\ definition,\ assumptions \rangle).

Ориентация пары по шкале:

(\mathrm{pol}(x,y;F)=\mathrm{sign}(F(y)-F(x)) \in {+1,-1}).

Порядок, индуцированный шкалой:

(x <_F y \Leftrightarrow F(x) < F(y)).

Этого достаточно, чтобы энтропийная стрела была машинно проверяемой как частный случай общей двухполярной схемы.

3) Роли анализатора и валидатора

Вариант B, который вы зафиксировали, здесь идеален.

Анализатор — «следователь». Он извлекает из текста утверждения (claims) и связывает их с объектами графа.

Валидатор — «судья». Он ничего не «понимает по-человечески», он проверяет строгие контракты типов и гейты, выдавая PASS/BLOCK/FAIL и минимальные требования к переписыванию.

4) Какие claims извлекать из текста про энтропию и время

Чтобы контур работал, анализатор извлекает атомарные утверждения в стандартизованном виде.

Минимальный набор claim-типов:

CLAIM_SCALE_DEFINED: “(S) определена как (k\ln W) при данном coarse-graining”. CLAIM_ORDER_BY_SCALE: “стрела/порядок задан через (S): (x<_S y)”. CLAIM_TYPICALITY: “рост (S) описывает типичность, а не логическую необходимость на каждой траектории”. CLAIM_IDENTITY: “(S) есть время” или “время = энтропия”. CLAIM_AGENT: “энтропия заставляет/двигает/принуждает” (реификация шкалы как агента). CLAIM_ABSOLUTE: “(S) всегда строго растёт” без условий. CLAIM_BOUNDARY: “стрела зависит от граничных условий/низкоэнтропийного старта” или, наоборот, “объясняет старт сама”.

Этого набора уже достаточно, чтобы отлавливать основной класс ложных парадоксов.

5) Как отличить корректную «энтропийную стрелу» от «клея»

Различение делается не «по вкусу», а по формальным признакам.

Корректная формулировка всегда имеет вид:

“(S) — шкала (F), которая задаёт ориентацию порядка или статистическую направленность переходов в выбранном режиме описания”.

Машинный критерий корректности:

Есть объект SCALE_ENTROPY (S). Есть объект ORDER (или порядок на событиях) и ссылка, что он индуцирован шкалой. Есть оговорка о режиме описания (coarse-graining) и о вероятностной природе (типичность), если обсуждается «всегда растёт».

Некорректная формулировка всегда имеет вид:

“(S) — сущность/агент/двигатель, который сам по себе является временем или заставляет мир идти”.

Машинный критерий некорректности:

Появляется CLAIM_IDENTITY (тождество типов). Появляется CLAIM_AGENT (шкала действует как агент). Появляется CLAIM_ABSOLUTE без ссылок на условия режима.

6) Гейты: что именно должно давать BLOCK/FAIL

Я предлагаю три обязательных гейта для этого участка теории.

GATE_TYPE_MIXING_TIME_SCALE. Срабатывает, если в claims присутствует тождество между объектами разных типов: TIME_ORDER и SCALE. Триггер: CLAIM_IDENTITY или эквивалентная связка “X = Y”, где X.type=TIME, Y.type=SCALE. Решение: BLOCK и требование переписать как “(S) индуцирует порядок/ориентацию”, а не “есть время”.

GATE_SCALE_REIFICATION. Срабатывает, если шкала используется как агент или субстанция. Триггер: CLAIM_AGENT или паттерны “энтропия заставляет”, “энтропия движет”, “энтропия хочет”, “энтропия является причиной как вещь”. Решение: BLOCK и требование заменить агентность на предикаты типичности и ограничения режима.

GATE_ABSOLUTE_MONOTONICITY. Срабатывает, если утверждается строгая монотонность (S) “всегда и везде” без условий. Триггер: CLAIM_ABSOLUTE при отсутствии CLAIM_TYPICALITY и CLAIM_BOUNDARY. Решение: FAIL, если контекст явно претендует на универсальный закон; иначе BLOCK и требование добавить условия: закрытая система, coarse-graining, статистическая типичность, оговорка о флуктуациях и о подсистемах.

7) Механика валидатора: краткий алгоритм проверки

Валидатор на вход получает claims, привязанные к графу, и контекст режима.

Шаг 1. Проверить типы: TIME — это порядок, SCALE — это функция. Шаг 2. Проверить, нет ли CLAIM_IDENTITY. Если есть, включить GATE_TYPE_MIXING_TIME_SCALE. Шаг 3. Проверить, нет ли CLAIM_AGENT. Если есть, включить GATE_SCALE_REIFICATION. Шаг 4. Если есть CLAIM_ABSOLUTE, потребовать CLAIM_TYPICALITY и CLAIM_BOUNDARY. Иначе включить GATE_ABSOLUTE_MONOTONICITY. Шаг 5. Сформировать минимальный план переписывания: какие claims надо добавить, какие переформулировать.

Это превращает «парадокс» в машинно-фиксируемое состояние BLOCK/FAIL с конкретной причиной.

8) Минимальные JSON-объекты для реализации

Ниже — минимально достаточные формы. Они не претендуют на ваш полный стандарт, но совместимы с логикой «следователь/судья».

Пример шкалы энтропии:

{ "scale_id": "SCALE_ENTROPY_BOLTZMANN_V1", "type": "SCALE", "domain_type": "MACROSTATE", "codomain_type": "REAL", "definition": "S(M)=k*ln(W(M))", "assumptions": [ "macrostate_partition_fixed", "W_defined_as_multiplicity" ], "notes": "Entropy as evaluation scale; not an agent." }

Пример claim «энтропийная стрела задаёт порядок»:

{ "claim_id": "CLAIM_ORDER_BY_SCALE_0001", "type": "CLAIM_ORDER_BY_SCALE", "subject": {"type": "ORDER", "id": "ORDER_TIME_T2"}, "predicate": "INDUCED_BY", "object": {"type": "SCALE", "id": "SCALE_ENTROPY_BOLTZMANN_V1"}, "formula": "x<_S y <=> S(x)<S(y)", "mode": "OIK", "confidence": 0.8, "evidence_refs": ["TEXT_SPAN_12_34"] }

Пример claim-ошибки «энтропия есть время»:

{ "claim_id": "CLAIM_IDENTITY_0007", "type": "CLAIM_IDENTITY", "lhs": {"type": "SCALE", "id": "SCALE_ENTROPY_BOLTZMANN_V1"}, "rhs": {"type": "TIME_ORDER", "id": "ORDER_TIME_T2"}, "surface_text": "энтропия и есть время", "mode": "UNKNOWN", "confidence": 0.9, "evidence_refs": ["TEXT_SPAN_55_63"] }

Пример результата валидации гейта:

{ "validation_id": "VAL_2025_12_23_001", "status": "BLOCK", "gate_hits": [ { "gate_id": "GATE_TYPE_MIXING_TIME_SCALE", "severity": "BLOCK", "trigger_claims": ["CLAIM_IDENTITY_0007"], "message": "Type mixing: TIME_ORDER cannot be identical to SCALE." } ], "rewrite_requirements": [ "Replace identity with induced order: x<_S y <=> S(x)<S(y).", "Add typicality clause: increase is statistical, not absolute." ] }

9) Рецепт автоматического переписывания (как валидатор возвращает текст без потери смысла)

Чтобы «судья» не только запрещал, но и возвращал пользователя к корректной формуле, нужен минимальный набор шаблонов.

Шаблон замены тождества:

Вместо “(S) есть время” нужно “(S) — шкала, индуцирующая ориентацию времени в выбранном описании: (x<_S y \Leftrightarrow S(x)<S(y))”.

Шаблон снятия агентности:

Вместо “энтропия заставляет” нужно “переходы типично ориентированы в сторону большей кратности (W), что выражается ростом (S=k\ln W)”.

Шаблон снятия абсолютности:

Вместо “(S) всегда растёт” нужно “в закрытых системах при фиксированном coarse-graining рост (S) является статистически типичным; флуктуации возможны; у подсистем локальное уменьшение совместимо с ростом энтропии окружения”.

Итог

Так энтропийная стрела времени становится не философской метафорой, а процедурой в машинном контуре:

1. анализатор извлекает claims о шкале (S), порядке и типичности;

2. валидатор проверяет, что “время” остаётся порядком, а “энтропия” остаётся шкалой;

3. гейты блокируют реификацию шкалы и смешение типов;

4. система выдаёт минимальный план переписывания, сохраняя смысл и убирая ложные парадоксы.

Следующий логический шаг — связать этот блок с модулем «дискретного градиента (-\nabla J)»: энтропию можно подключить как частный вклад (J)-компоненты, где «гравитационность» становится не силой, а направлением уменьшения рассогласования, а энтропийная шкала — одним из допустимых (F) в двухполярной проекции.

Если есть вопросы, просто загрузите архив и вставьте в чат ChatGPT. Далее достаточно написать: «Архив во вложении. Старт: следуй NAVIGATOR_NEXTCHAT_NETWORK_THINKING_iter355.md »

Читать далее:

Что такое время в двухполярной (обыденной) модели и почему это определение выигрывает у «метафизических» теорий

Природа времени и гравитации. Простая и ясная теория

Троица в христианстве: как L3-логика снимает видимость противоречий

Что такое разум с позиции L3-логики, или как «Алмазная сутра» учит нас разуму

Ноль и единица в трёхполярной логике: почему бинарность недостаточна и как работает трёхполярный гиперграф

Трёхполярный гиперграф L3 v0.1.0: нелинейная многополярная система, которая объясняет всё — от ИИ до солнечных циклов

1. Минимальное определение двухполярного времени

Я начинаю с множества событий.

E — множество событий (в широком смысле: фактов, действий, состояний, актов фиксации).

Далее я ввожу бинарное отношение «раньше».

Обозначу его так: a < b, читается «a раньше b».

Двухполярное время — это структура (E, <), удовлетворяющая минимальным аксиомам упорядочивания.

А1. Антирефлексивность: не существует a, такого что a < a. А2. Транзитивность: если a < b и b < c, то a < c.

Если я хочу именно «обыденную ось», где любое два события сравнимы, я добавляю:

А3. Сравнимость: для любых a и b либо a < b, либо b < a, либо a = b.

Тогда < становится строгим линейным порядком, то есть формальной моделью привычной линии времени.

Смысл этого определения принципиален: я не утверждаю, что «время — вещь». Я утверждаю, что «время» в обыденном режиме — это правило сравнения событий по порядку.

2. Измерение времени как вторичная надстройка

Обыденное мышление обычно путает два слоя: порядок и измерение. Порядок отвечает на вопрос «что раньше?», а измерение — «на сколько раньше?».

Чтобы добавить измерение, я ввожу отображение:

t: E -> T,

где T — числовая шкала (обычно подмножество вещественных чисел), и требую монотонности:

если a < b, то t(a) < t(b).

Это ключевой момент: числовое время t не первично; оно является координатизацией уже заданного порядка. В повседневности роль t выполняют часы и календарь, но их смысл состоит в том, чтобы стабильно репрезентировать отношение <.

Таким образом, двухполярное время имеет два уровня:

Порядок: (E, <). Метрика-координата: t, согласованная с <.

3. «Настоящее», «прошлое», «будущее» как производные, а не сущности

Обыденное сознание склонно реифицировать «настоящее» как особый объект. Но в рамках двухполярного определения это всего лишь выделение точки отсчёта.

Пусть выбран опорный момент n (или событие now). Тогда:

Past(now) = { a из E | a < now } Future(now) = { b из E | now < b }.

То есть «прошлое» и «будущее» — это не царства бытия, а множества событий, определённые относительно выбранного now.

Это снимает значительную часть псевдо-мистики: прошлое и будущее не требуют отдельной онтологии, чтобы быть осмысленными в обыденном режиме. Их достаточно определить через <.

4. Чем это определение лучше распространённых теорий

Ниже я сравниваю не «истинность» теорий, а полезность определения как рабочего основания. Моя цель — показать преимущество минимальной двухполярной формализации как базовой дисциплины мысли.

4.1. Против времени как субстанции

В классическом ньютоновском воображении время нередко понимается как нечто абсолютное, существующее «само по себе». Это удобно риторически, но дорого онтологически: мы вводим сущность, которую невозможно наблюдать иначе как через процессы.

Двухполярное определение выигрывает тем, что не требует субстанции времени. Я могу иметь порядок событий и шкалу t как согласованную координатизацию, не принимая метафизического тезиса «время существует отдельно от событий». Если кому-то нужен ньютоновский смысл, он может интерпретировать < как проявление абсолютного времени, но определение от этого не зависит.

Преимущество: онтологическая экономия без потери операциональности.

4.2. Против времени как чистого отношения без формализации

Лейбницианский (реляционный) подход говорит: время — это порядок последовательностей изменений. Это близко к моей позиции, но часто остаётся на уровне слов. Моя версия делает реляционность строгой: отношение < — явный объект теории, с аксиомами и критериями корректности.

Преимущество: реляционизм становится исполняемым, проверяемым и пригодным для вычисления и протоколирования.

4.3. Против времени как исключительно субъективной длительности

Интуитивистские и феноменологические традиции (в предельной форме — «время как переживание длительности») важны для антропологии, но они плохо работают как основание для согласования разных наблюдателей и разных дисциплин. Переживание не даёт строгого критерия, что считать «раньше» в коллективной реконструкции.

Двухполярное определение не отрицает субъективный опыт; оно просто не делает его фундаментом. Оно задаёт межсубъектный каркас: порядок событий, который может быть разделён и проверен.

Преимущество: совместимость с коллективной рациональностью и научной процедурой.

4.4. Против метафизических конфликтов «становление/блок»

В философии времени известен раскол между трактовками «время как становление» и «время как статическая структура». Во многих вариантах этот спор зависит от того, смешиваются ли разные типы предикации: описываем ли мы порядок событий, или утверждаем особый онтологический статус «настоящего».

Моё определение выводит «настоящее» как производную от выбора now, а не как сущность. Поэтому значительная часть конфликта становится вопросом интерпретации, а не логической необходимости. Я сохраняю модель порядка и шкалы, а онтологические добавки оставляю факультативными.

Преимущество: спор переводится из области «обязательных сущностей» в область «дополнительных интерпретаций».

4.5. Согласование с физикой и ограничение «тотальности»

Важно честно сказать: в физике, особенно в релятивистской картине, глобальный тотальный порядок событий не всегда допустим. То есть аксиома А3 (сравнимость любых двух событий) может быть неверна глобально.

Но и здесь двухполярное определение выигрывает: я явно вижу, где именно я добавляю сильное предположение. Если А3 снимается, я получаю частичный порядок (E, <), и это всё равно остаётся двухполярной структурой в смысле «раньше/позже», просто без тотальности. Локально вдоль наблюдаемой последовательности (например, вдоль «траектории опыта» или вдоль согласованной процедуры измерения) тотальный порядок восстанавливается.

Преимущество: определение масштабируется от бытового времени к строгим частичным порядкам, не ломаясь и не требуя новой метафизики.

5. Главный выигрыш: время как дисциплина сравнения, а не как «вещь»

Я считаю главным достоинством моего определения следующее.

Двухполярное время — это минимальная дисциплина сравнения событий, задаваемая отношением < и, при необходимости, координатизацией t.

Эта дисциплина даёт сразу три практические выгоды.

Она делает время проверяемым: можно спорить о том, существует ли порядок < между двумя событиями и по каким источникам он устанавливается.

Она отделяет порядок от меры: можно иметь «что раньше» без «сколько прошло» и не смешивать эти уровни.

Она предотвращает «клей»: время перестаёт быть объяснительным магическим словом. Если мы не можем согласовать порядок, мы не обязаны прибегать к метафизике; мы обязаны признать, что данных недостаточно или что режим описания не определён.

6. Граница применимости двухполярного времени

Преимущество определения не означает универсальности. Двухполярное время специально хорошо там, где требуется линейная реконструкция и отчётность: быт, история, протоколы, алгоритмы, проектное управление.

Оно хуже схватывает то, что требует многомерной причинности, режимных переключений и триадных замыканий. Там уже уместна трёхполярная перспектива, где «время» становится производной режима. Но важно другое: двухполярное время остаётся базовой проекцией, которую можно честно включать и честно ограничивать.

Заключение

Я определяю двухполярное (обыденное) время как структуру упорядочивания событий (E, <) с возможной координатизацией t, согласованной с этим порядком. Это определение выигрывает у многих традиционных теорий тем, что оно минимально, операционально, межсубъектно и онтологически экономно. Оно позволяет работать с временем как с дисциплиной сравнения, а не как с загадочной сущностью, которая объясняет всё и потому не объясняет ничего.

Библиографические ориентиры

Ньютон И. Математические начала натуральной философии. Лейбниц Г. В. Переписка с Кларком о пространстве и времени. Кант И. Критика чистого разума (раздел о времени как форме созерцания). Бергсон А. Творческая эволюция; Материя и память (длительность). Эйнштейн А. Изложения специальной и общей теории относительности (о времени и одновременности). Мак-Таггарт Дж. Э. «Нереальность времени» (A- и B-серии).

Если есть вопросы, просто загрузите архив и вставьте в чат ChatGPT. Далее достаточно написать: «Архив во вложении. Старт: следуй NAVIGATOR_NEXTCHAT_NETWORK_THINKING_iter355.md »

Читать далее:

Природа времени и гравитации. Простая и ясная теория

Троица в христианстве: как L3-логика снимает видимость противоречий

Что такое разум с позиции L3-логики, или как «Алмазная сутра» учит нас разуму

Ноль и единица в трёхполярной логике: почему бинарность недостаточна и как работает трёхполярный гиперграф

Трёхполярный гиперграф L3 v0.1.0: нелинейная многополярная система, которая объясняет всё — от ИИ до солнечных циклов

Время - относительная скорость процессов. Только и всего. Откуда и куда там "перемещаться"?

Управлять временем, при этом, вполне возможно, влияя на скорость процессов. Если их затормозить, время будет идти медленнее, если ускорить - быстрее. Но обратно - никак. Хотя вернуть систему в то же состояние, в котором она была в прошлом, можно. Если воду разморозить, а потом снова разморозить, это не тот же кусок льда, который был.

Если человек прошёл по полю туда и обратно, то можно измерить расстояние, сопоставив с эталоном метра, и время, сопоставив с движением Солнца, но человек не перемещался в метрах и минутах. Потому что их нет.