Привет. С вами снова я, со своей низкочастотной приблудой. В прошлом посте я обещал рассказать о том, что я там напринимал.
Так вот, вынужден всех разочаровать, в этом посте не будет много крутой инфы и дешифровки военных сигналов. Скорее это будет обзор, что же все-таки приблуда может и, в основном, чего не может. Я хотел найти какую-нибудь прогу получше Audacity для анализа записанных сигналов, но че-то под венду ничего толкового не нашел, может быть, кто-то в комментах что-то посоветует, так что нам придется довольствоваться скринами с телефонного Spectroida`a. Я попробовал SDR#, но, блин, он какой-то кривой и покрашился у меня при попытке воспроизвести файл, так что я во гневе его сразу снес. Ну ладно, хватит отмазок, переходим к делу.
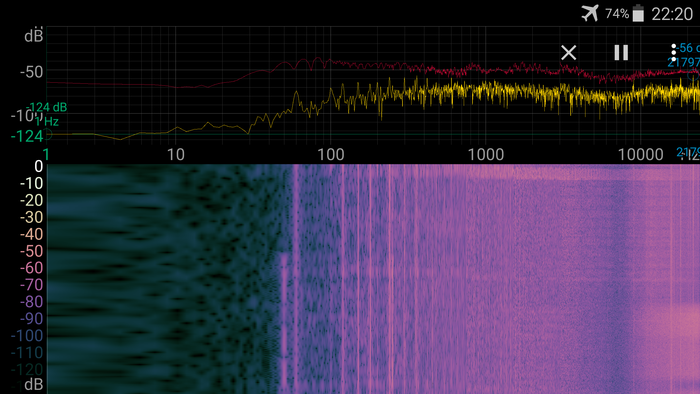
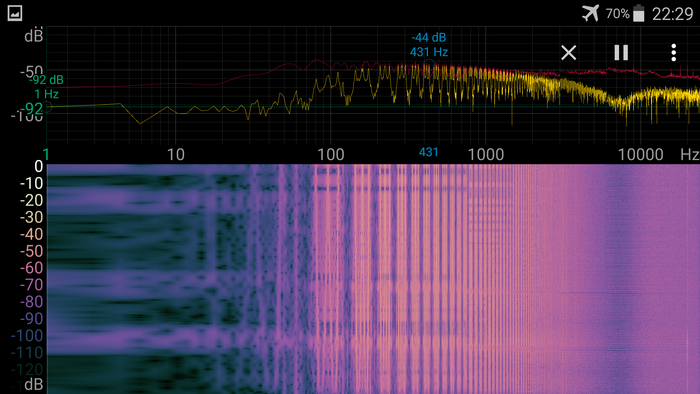
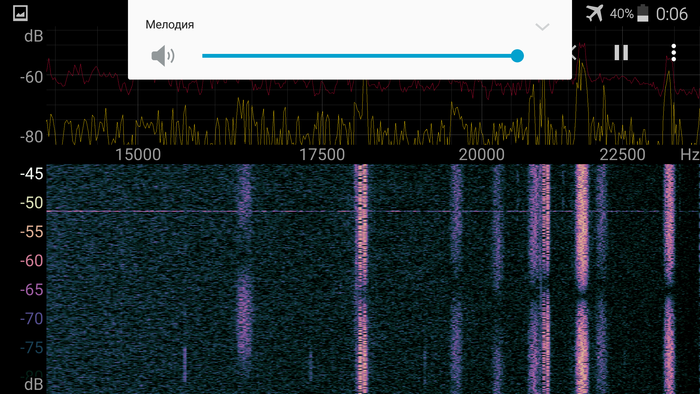
Вот это - общий обзор, так сказать, спектра. Ниже примерно 60 герц низкий уровень даже шума, потому что в приблуде стоит ФВЧ, кроме того, есть подозрение, что в мобиле тоже. Ничего ниже этого порога принять невозможно. Дальше можно видеть, что идут довольно яркие полосы с частотой, кратной 60Гц - это помехи от мобилы. Там что-то генерит, насколько я понял, 60-герцовый меандр, который, видимо, используется для работы экрана и тачскрина. При перевороте мобилы появляются дополнительные полосы, в некоторых случаях нажатие на экран так же заметно на спектре. Вот эта вот вся беда продолжается наверно килогерц до шести, так что этот дипазон моей приблуде так же недоступен - все забито помехами от мобилы. Вероятно, при более аккуратном изготовлении, при добавлении нормальных фильтров по питанию(и сигналу), при использовании более подходящего ОУ (или можно попробовать этот усилитель запитать более высоким напряжением, но мне страшно, что можно че-нето в мобилке пожечь) можно было бы избавиться от этих помех и расширить полезный диапазон. Кстати, вы можете видеть в правом нижнем углу картинки, что там шум на высоких частотах был несколько сильнее. Это так же шум от мобилы, но принимаемый, судя по всему, уже самой антенной, так как его можно снизить, просто подбирая положение и ориентацию телефона относительно антенны.
А вот это умиротворяющее зрелище с низким уровнем шума - это то, что получается, если отключить питание ОУ. Как можно видеть, помехи от мобилы все равно пробиваются.
Вот этот скрин без ничего, кроме телефонных помех - это я положил антенну горизонтально на капот машины. В таком положении антенна экранируется капотом, кроме того поляризация большинства сигналов в этом случае становится параллельной плоскости антенны, следовательно они перестают приниматься. Как известно, сигналы СДВ имеют в основном линейную вертикальную поляризацию по электрическому полю, так как горизонтальная компонента, если таковая есть, быстро поглощается земной поверхностью. Таким образом можно оценить уровень разнообразных шумов, который, как мы видим, просто ужасающий и ни о каком приеме слабых сигналов не может идти и речи.
А вот такое получается, если засунуть внутрь антенны включенную Glo. У меня версия, которая, как утверждает производитель, использует индукционный нагрев, ну и судя по тому, как она фонит, похоже, что производитель не врет.
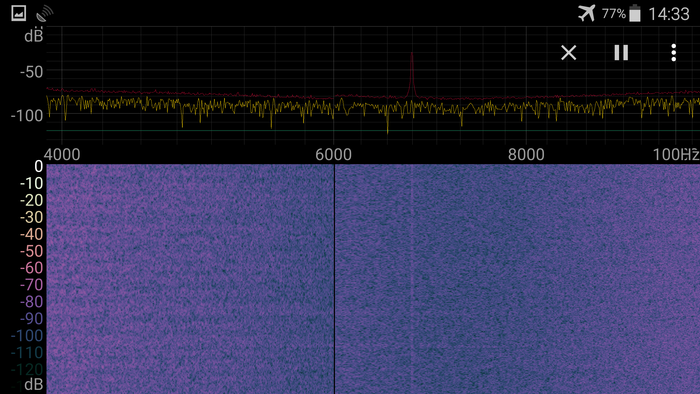
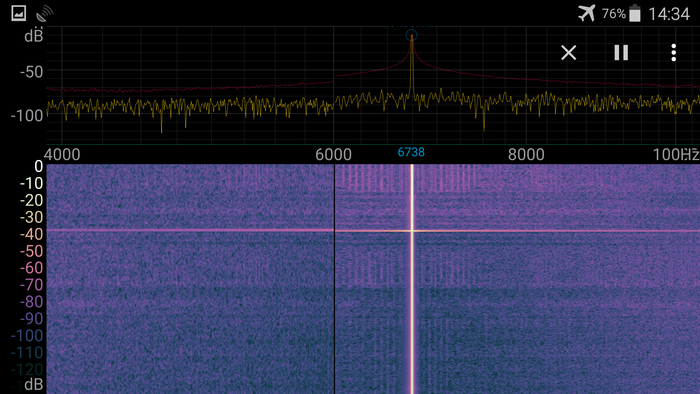
А вот эти два скрина как бе показывают нам, что будет, если отключить антенну. На верхнем антенна просто отключена, а на нижнем контакты антенны замкнуты накоротко.
У меня еще были скрины со сравнением шумов с питанием от батарейки и от USB, но они к сожалению, где-то потерялись. Так что придется вам поверить(или нет) мне на слово, что с питанием от батарейки шумы немного(но незначительно) пониже, а так же меньше влияние ориентации мобилы на антенну. Кроме того, батарейки выдают 6 вольт против 5 на USB, что, видимо, тоже немного улучшает общую картину.
Ну да ладно, шумы - это, конечно, очень интересно и весело, но, может быть, пора уже перейти к каким-нибудь сигналам?
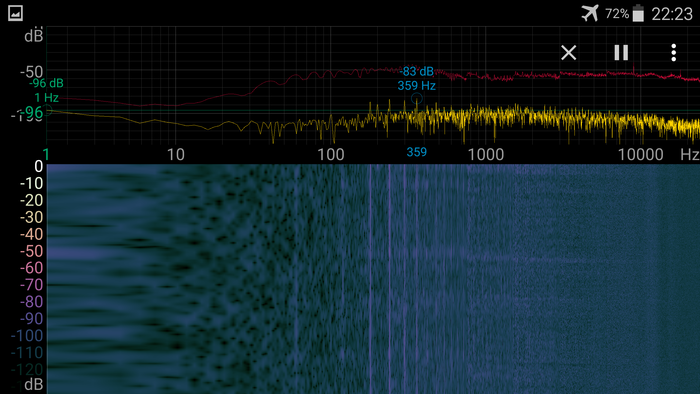
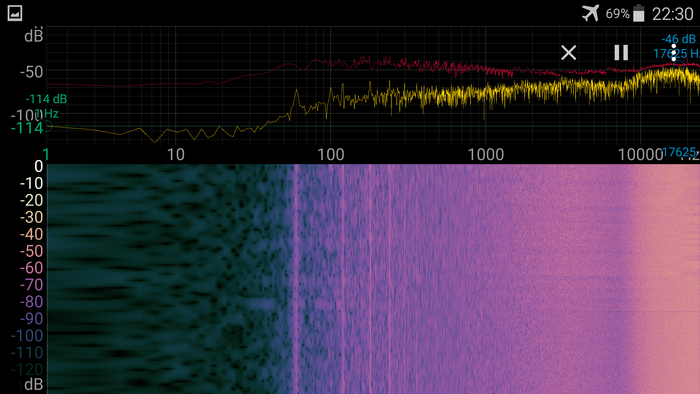
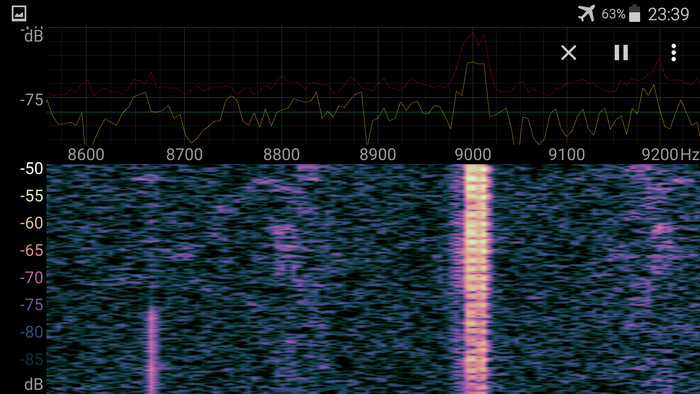
Вот эта картинка - характерный пример того, что приблуда все-таки принимает, и что не является совсем уж шумом.
На частоте ровно 9КГц (и, я подозреваю, на 18Кгц - его же обертон) находится ТАИНСТВЕННЫЙ сигнал!!!! Вы можете видеть его линию примерно по центру картинки. Я так и не понял, что это и откуда, и даже гугление не помогло. Запеленговать этот сигнал невозможно, он практически всегда есть, и на дачном участке, и в поле вдалеке от населенных пунктов, но его поляризация, как и у прочих сигналов, вертикальная, так как он пропадает, если держать антенну параллельно земле.
Дальше у нас огромный, мощный и страшный сигнал из множества линий с центром на 15,7 КГц. Это так в эфир(и в сеть) срёт светодиодный драйвер от фонаря уличного освещения. Сигнал хорошо слышно у самого фонаря, а так же при приближении к проводам.
Дальше у нас, начиная где-то с 18КГц идут настоящие сигналы радиостанций. Они, в смысле, радиостанции, расположены в разных местах и используют, судя по всему частотную манипуляцию для передачи данных, в эфире они практически постоянно. Возможно, это какие-то маяки.
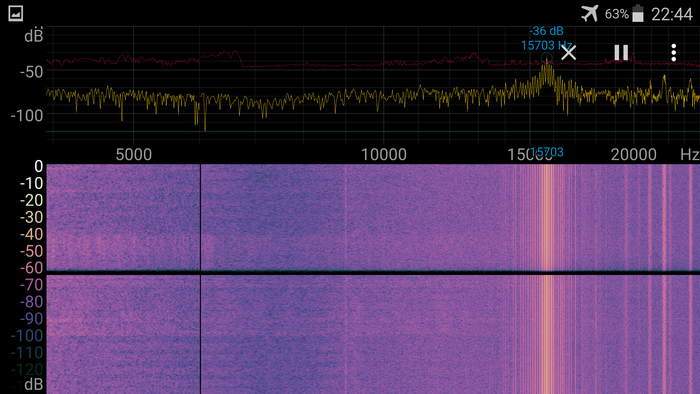
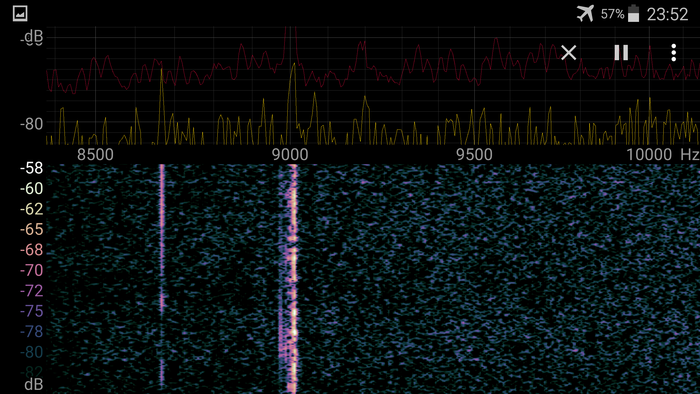
Вот пара картинок с таинственным сигналом, которые сделаны с более высоким спектральным разрешением. Мои лучшие предположения насчет этого сигнала - какие-нибудь маяки, а не пеленгуется, потому что их несколько и сигнал принимается одновременно с разных направлений.
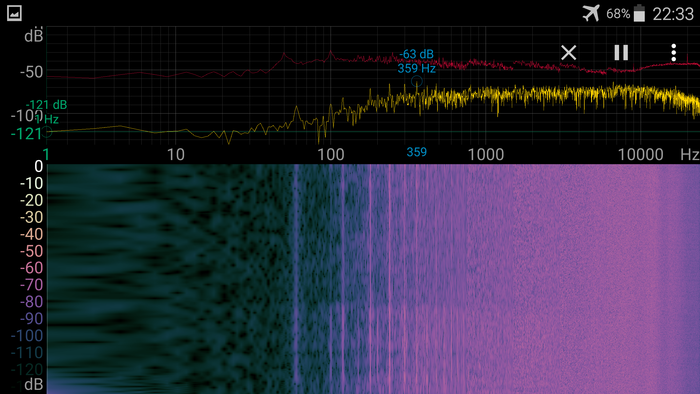
А вот здесь, помимо каких-то сигналов, в которых я не стал разбираться, так как они принимаются непонятно как - то есть, то нет, можно увидеть горизонтальные полосы. Есть мнение, что это всплески от далеких грозовых разрядов, хотя лично я лично не полностью в этом уверен, так как у меня возможно просто где-то провода питания на приблуде плохо контачат.
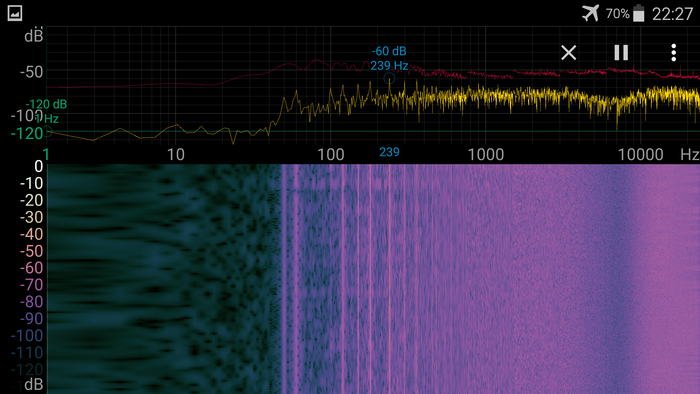
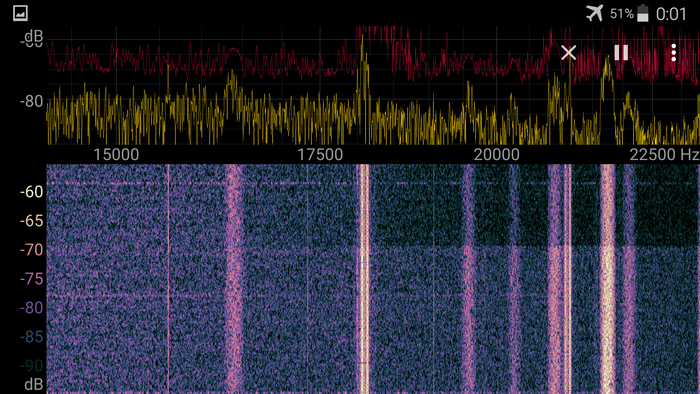
А вот тут у нас два самых ярких сигнала на 18.1КГц и 21.1 - это сигналы радиостанции RDL, про которую можно почитать в интернете. На 18 КГц она передает практически постоянно, у ней высокая мощность, ее можно хоть для навигации использовать, на 21 - намного реже. Она использует частотную манипуляцию, передает иногда азбукой морзе, иногда каким-то другим методом, есть мнение, что это радиостанция в Нижнем Новгороде. Что за остальные широкие полосы здесь - я при помощи интернетов не смог это выяснить, они, вероятно, используют квадратурную модуляцию или вообще что-то другое. Но я уверен, что это так же настоящие радиостанции, а не какие-то помехи, так как они хорошо пеленгуются.
А вот здесь можно видеть, как антенна пеленгует. "Водопад" охватывает интервал времени примерно 10 секунд. За это время я медленно поворачивал антенну. У антенны в диаграмме направленности есть два резких минимума, то-есть если она перестала принимать сигнал, значит, ее плоскость повернута практически точно перпендикулярно к направлению на сигнал. Можно видеть, что минимумы разных полос не совпадают, значит, они находятся в разных местах, Направление, вдоль которого большинство станций перестает слышаться - это направление Москва - Нижний Новгород, разброс составляет порядка 20-30 градусов. Так что вывод о координатах станций начинающие диванные шпиёны могут сделать сами.
А вот это - сигнал от металлоискателя. Снизу - прям рядом с прибором, а сверху - на расстоянии примерно 30 метров от него. Запеленговать металлоискатель при помощи моей приблуды невозможно, так как у него поляризация(если он, как и положено, направлен в землю) горизонтальная, так что для приема антенна должна быть направлена параллельно земле, ну и, соответственно, поворачивать ее не имеет смысла.
Вот вам еще архив записей, может, кто-то захочет сам поанализировать, че там да как. Можно их просто послушать, там среди помех иногда голоса слышно - не беспокойтесь, это не феномен электронного голоса, это принимаются какие-то то-ли китайцы, то-ли французы. Я, честно говоря, не понял, как они там оказались, буду благодарен, если кто-то подскажет, почему так и как от них избавиться.
Ну штош, на сегодня все.
P.S. Хочу извиниться перед всеми, кто мне задавал какие-то вопросы в комментах к предыдущему посту, а я не ответил - не было времени. В этот раз я постараюсь ответить на как можно большее число вопросов.
Кроме того, хочу поблагодарить всех, кто давал дельные советы. Я вас запомнил! Зачем, спросите вы? А дело в том, что я собираюсь запилить новую приблуду, но уже более толковую, на частоту от 0 до 1 МГц с отдельным АЦП, ибо как раз с 1 МГц начинаются многие SDR-свистки, которые можно купить. А меньший диапазон можно и самоделкой попробовать охватить. Так что дельные советы мне очень сильно пригодятся.
P.P.S. Хочу обратиться к админам лиги радиолюбителей. Посты на премодерации находятся сутки и больше - вы с правительством, что-ли, их содержание согласуете? Это же небольшое нишевое комьюнити, зачем вообще здесь премодерация? Отключите ее, и не морочьте голову ни себе, ни пользователям, пожалуйста.