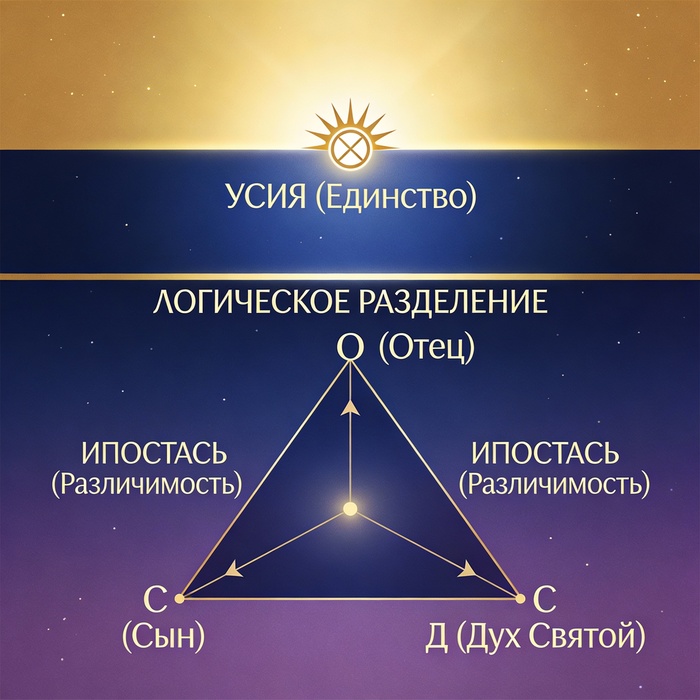
Почему трёхфазная система не является строгой трёхполярностью (L3): Z3-структура против трёхканальной L2-проекции
Введение. Почему трёхфазная система не является строгой трёхполярностью (L3)
В инженерной практике трёхфазная система выглядит как “естественная триада”: три обмотки, три токовых канала, сдвиг на 120°, симметрия перестановки фаз, устойчивое вращающееся поле. Поэтому соблазнительно сделать короткий вывод: раз в трёхфазке работает триада и поворот на 120°, значит она и есть “трёхполярность” (L3) в строгом смысле.
Я утверждаю обратное: трёхфазная система активно использует симметрию Z3 (перенумерацию фаз), но онтологически она не фиксирует трёхполярное состояние L3. Она реализует L2-наблюдаемое: набор измеримых чисел (амперы/вольты), из которых стандартной редукцией выделяется двухкомпонентное состояние (квадратурная плоскость, “пространственный вектор”), а триада остаётся способом организации каналов и симметрий, но не базовой алгеброй состояния.
Ключевой методологический разрыв здесь такой.
Z3 в трёхфазке — это симметрия перестановки меток, то есть допустимая перенумерация каналов (A,B,C) и поворот “на 120°” в модели. Это мощная и реальная инвариантность, она лежит в основе баланса, гармоник, расчётов вращающегося поля и устойчивости привода.
L3 в строгом смысле — это не “три канала” и не “три синуса”, а алгебра отношений на множестве полярностей P3 = {p0,p1,p2} с заданной бинарной операцией a ⊙ b ∈ P3, ковариантностью относительно Sym3 и, в физически-подобной постановке, с локальным носителем и операторами источниковости/контурности, где возникают проверяемые инварианты вида D * R^T = 0. То есть L3 — это структура состояния, а не форма представления сигналов.
Трёхфазка почти всегда “схлопывается” в двухмерное описание: либо явно (через базисные преобразования в двумерную плоскость), либо неявно (через энергетические/мощностные функционалы, которые чётны по знаку и фазе). Это принципиально: состояние трёхфазной машины живёт не в “чистой триаде”, а в пространстве, где естественно присутствует квадратура, а вместе с ней — ветвление ориентации и инволюции (то, что в моей дисциплине относится к L4-слою “состояние/наблюдаемое”).
Отсюда следует практический тезис, который и делает статью полезной инженеру, а не философу: трёхфазка использует триаду как симметрийный интерфейс, но строгая трёхполярность требует триады как онтологии и алгебры состояния. В реальной технике триадный интерфейс почти всегда измеряется и управляется через L2-проекцию; поэтому “три” там — не фундамент алгебры, а организация измерительных каналов.
Дальше я разверну это без метафор, через определения и инварианты.
Глава 1: я фиксирую, что именно означает “строгая трёхполярность” (L3): P3, Sym3/Z3, операция ⊙, ковариантность, и почему триада даёт механизм локального ремонта (а пара — нет) на уровне структурной достаточности.
Глава 2: я показываю, что трёхфазная система по своей математике является L2-наблюдаемой: токи i_a(t), i_b(t), i_c(t) — числа, а “существенное состояние” выделяется как двумерный объект; симметрия Z3 сохраняется, но она действует как перенумерация представления, а не как алгебра состояния.
Глава 3: я формулирую критерий различения “Z3-симметрии в сигнале” и “L3-онтологии поля” и показываю, почему строгость L3 не заменяется трёхфазкой, а трёхфазка, наоборот, естественно живёт в паре L3+L4: L3 как симметрийный каркас взаимодействий и L4 как слой ветви/инволюции и разделения “состояние/наблюдаемое”.
Глава 1. Что я называю строгой трёхполярностью (L3) — и почему “три канала” этим не становятся
1. Минимальная онтология L3: не три сигнала, а три полярности
Трёхполярность (L3) начинается не с синусов и не с проводов. Она начинается с факта:
есть множество полярностей P3 := {p0, p1, p2},
и существует правило отношения (бинарная операция) ⊙ : P3 x P3 -> P3,
которое считается первичным объектом теории.
Важно: p0, p1, p2 — не числа и не “фазы” в инженерном смысле. Это метки структурно различимых состояний/полюсов/полярностей. Числа появляются позже — как измерительная проекция (уровень L2).
Если дальше нет операции ⊙ (или её таблицы), то “три” остаётся косметикой: три канала, три датчика, три обмотки. L3 там не начиналась.
2. Симметрия L3: что считается допустимой перенумерацией
В L3 есть принципиальный класс преобразований: перенумерация полярностей, то есть действие группы симметрий на P3.
Полная группа переименований: Sym3 = S3 (все перестановки трёх меток).
Частный и наиболее часто встречающийся подслучай: Z3 (циклический поворот) p0 -> p1 -> p2 -> p0.
Теперь центральный критерий.
Аксиома (ковариантность/инвариантность таблицы): если g — допустимая симметрия, то правило отношения должно “переживать” переименование:
g(a ⊙ b) = (g a) ⊙ (g b).
Это означает: симметрия действует не только на “ярлыки”, но и на сам закон.
В трёхфазке Z3 действительно присутствует — но чаще всего как симметрия представления сигналов (переставили фазы, переписали формулы). В строгой L3 Z3 — это симметрия, которая ограничивает, что вообще является допустимым взаимодействием.
3. Алгебра L3: почему “2×2≠4” — не шутка, а следствие типизации
В L2 “2×2=4” имеет смысл, потому что числа живут в поле/кольце, и умножение — операция в том же множестве чисел.
В L3 “2” и “4” как числа вообще не обязаны существовать. У нас есть только три полярности p0,p1,p2. Поэтому корректный вопрос звучит так:
чему равно p_i ⊙ p_j?
Если вы ради интуиции кодируете полярности числами 0,1,2, то это не делает L3 арифметикой целых. Например, вы можете задать операцию как сложение по модулю 3:
encode(p_k)=k,
p_i ⊙ p_j := decode((i+j) mod 3).
Тогда:
p_1 ⊙ p_1 = p_2, и в “числовой маске” это выглядит как “1+1=2”, но это не “арифметика натуральных”; это работа внутри трёх состояний.
В этом смысле фраза “в L3 дважды два не равно четыре” переводится на строгий язык так:
в L3 нет числа 4 как элемента P3,
а повторная композиция “двойки” — это не умножение натуральных, а применение ⊙ в конечной системе.
Если операция ⊙ у вас не задана, то вы не имеете права делать такие выводы вообще. Поэтому в моём подходе L3 начинается с янтры/таблицы.
4. Что такое “трёхполярное поле” и “трёхполярный ток” в строгом смысле
Чтобы не путаться с электротехникой, я фиксирую определения в структурной форме.
4.1. Трёхполярное поле (Field_L3)
Трёхполярное поле — это не функция R^3 -> R. Это:
носитель (граф/решётка/клеточный комплекс) X,
значение поля на элементах носителя (например, на рёбрах или вершинах) в множестве полярностей: F: X -> P3,
и закон композиции ⊙, который определяет, как локальные состояния “склеиваются” или “составляются” при обходе/сшивке (в зависимости от выбранного уровня локальности).
То есть поле хранит состояние в трёхполярной онтологии, а не вещественную амплитуду.
4.2. Трёхполярный ток (Current_L3)
Трёхполярный ток в моём смысле — это не амперметрическое число. Это:
локально определённый “поток изменения” состояния поля, который тоже живёт в P3 (или в типизированной структуре над P3, если вводится направленность/ориентация),
и который связан с дефектами/источниками через оператор источниковости (аналог D в дискретной схеме).
На этом уровне ток — это объект согласования: он фиксирует, как изменения распределяются по носителю так, чтобы не возникало фиктивных источников от контуров (идея, которая дальше оформляется через инварианты локальности).
Ключевое: в L3 “ток” — это элемент структурного языка, а амперы — это уже L2-проекция измерения.
5. Почему триада даёт “локальный ремонт”, а пара — нет
Разберем, почему триада принципиально сильнее пары именно как механизм ремонта и согласования.
5.1. Пара (L2) даёт только инволюцию
В L2 есть два состояния: “+/-”, “0/1”, “да/нет”. Единственная нетривиальная симметрия — инволюция (обмен местами). Это даёт резкие, но бедные возможности:
любая ошибка часто выглядит как “перевернул знак”,
исправление часто сводится к “верни знак”.
Этого достаточно для контроля, но недостаточно для локальной реконфигурации, потому что нет третьего состояния, куда можно “вынести” конфликт, не ломая остальное.
5.2. Триада (L3) вводит третий режим как буфер согласования
Третий полюс в L3 играет роль структурного буфера:
при конфликте двух полярностей можно перейти в третий режим, который не является ни одним из конфликтующих,
и затем вернуться в согласованное состояние без глобальной переклейки.
Это и есть логика “локального ремонта”: конфликт не требует тотального сброса или тотальной перекоммутации — он может быть локально “погашен” через третий полюс, сохранив симметрийные инварианты.
Физически-инженерная аналогия (осторожная, но полезная): в трёхфазной системе при симметрии и правильной топологии многие перекосы можно локально компенсировать перераспределением по трём каналам, не разрушая режим работы целиком. Но — и это важно — в трёхфазке это компенсация чисел в L2-модели, а в L3 это компенсация состояний.
6. Почему трёхфазка всё же не является L3: критерий “нет операции — нет алгебры”
Теперь я фиксирую тот критерий, который потом станет стержнем всей статьи.
Трёхфазная система в реальности задаётся:
тремя измеримыми сигналами i_a(t), i_b(t), i_c(t),
линейными связями (сумма токов, матрицы преобразований),
инвариантами мощности/энергии,
симметриями перестановки фаз и поворота на 120°.
Это всё прекрасно и строго — но это строгость L2 (строгость числовых моделей), усиленная симметрией Z3.
Чтобы это стало строгой L3, нужно предъявить другое:
P3 как состояние (а не как три канала измерения),
операцию ⊙ как закон взаимодействия полярностей,
ковариантность этого закона относительно Sym3/Z3,
локальный носитель и согласованность “контуров/источников” (если мы говорим о поле, а не о голой алгебре).
В обычной трёхфазке пункт (2) отсутствует: там нет трёхполярной операции на состояниях, потому что базовый объект — вещественный сигнал. Поэтому трёхфазка не L3, хотя активно использует Z3.
Дальше логика такая: в главе 2 я покажу на уровне формул и инженерных преобразований, где именно трёхфазка неизбежно сворачивается в двумерное состояние (и почему это уже не “чистая триада”), а затем в главе 3 дам практический тест: что нужно добавить к трёхфазной картине, чтобы получить строгое L3-поле и L3-ток в моём смысле (и почему без L4 слой “ветви/наблюдаемого” всё равно будет всплывать).
Глава 2. Где именно трёхфазка “сворачивается” в L2, даже если в ней есть Z3
В главе 1 я зафиксировал критерий: строгая L3 начинается там, где задана трёхполярная онтология P3 и операция ⊙ на состояниях. В этой главе я делаю следующий шаг: показываю на физике трёхфазных систем, почему наличие Z3 (поворота на 120°) ещё не означает L3, и где именно трёхфазка практически всегда реализует L2-слой с симметрией Z3.
1. Z3 в трёхфазке: это симметрия представления, а не онтология состояния
В идеальной симметричной трёхфазной системе есть естественная циклическая симметрия:
перестановка фаз a->b->c->a соответствует повороту на 120°,
уравнения и энергетические балансы в идеальном режиме инвариантны к такому переименованию.
Это действительно Z3 как группа преобразований. Но вопрос, который решает всё:
Z3 действует на ЧТО именно?
В инженерной трёхфазке Z3 действует на вектор измеримых величин (напряжения/токи трёх проводов, их комплексные амплитуды, фазоры и т.д.). Это действие на координаты описания режима.
В строгой L3 Z3 должно действовать на полярности P3 как на первичные состояния, и при этом закон взаимодействия ⊙ обязан быть ковариантным:
g(a ⊙ b) = (g a) ⊙ (g b).
В трёхфазке “закон взаимодействия” — это не операция на трёх состояниях, а линейная динамика/связи на непрерывных величинах (R, L, C, матрицы, операторы). Это другой тип объекта: L2-математика, не L3-алгебра полярностей.
2. Ключевой факт: симметричная трёхфазка живёт в двумерном подпространстве
Это центральный пункт, который обычно знают инженеры, но редко связывают с философией “полярностей”.
Если система сбалансирована (идеально или близко), то три фазных величины удовлетворяют соотношению:
i_a + i_b + i_c = 0 и аналогично для напряжений в зависимости от схемы.
Это означает: физически “рабочая” часть режима живёт не в 3D, а в 2D, потому что одна линейная комбинация фиксирована (равна нулю). Геометрически:
пространство (i_a, i_b, i_c) трёхмерно как координатное,
но балансный режим лежит в плоскости i_a+i_b+i_c=0 (двумерная плоскость).
То есть “три фазы” в симметричном режиме реализуют двухмерное представление. Именно поэтому:
существует стандартное преобразование Кларка (abc -> alpha-beta-0),
и нулевая компонента (0-sequence) в идеале равна нулю,
а вся динамика (в симметричном режиме) описывается двумя координатами (alpha, beta).
И вот здесь точка, где трёхфазка объективно “сворачивается” в L2:
базовый объект — двухмерный вектор (alpha, beta),
который можно эквивалентно представить как одну комплексную амплитуду.
Факт “трёх фаз” остаётся как удобное трёхканальное представление, но онтология режима в симметричном случае — двумерная.
3. “Комплексные числа” в трёхфазке — не L3, а удобная упаковка L2
Инженерный язык фазоров часто использует комплексную плоскость: это делает расчёты проще.
Но важно: здесь “i” (мнимая единица) — это координатный трюк для 2D-представления, возникающего из синуса и косинуса (двух ортогональных компонент). Это не “четырёхполярность” и не “трёхполярность” как онтология состояний.
Другими словами:
комплексное представление в трёхфазке — это упаковка двумерной физики;
трёхфазка не становится “трёхполярной” просто потому, что в ней есть поворот на 120°.
Поворот на 120° — это элемент группы вращений в плоскости (в соответствующем представлении), а не операция на трёх дискретных полярностях.
4. Три “фазы” ≠ три “полярности”: различие в объекте и в допусках
Я фиксирую различие в самом прямом виде.
4.1. В трёхфазке базовый объект — непрерывная величина
Токи/напряжения — это функции времени, действительные или комплексные, и их закон — это:
линейные дифференциальные уравнения,
матричные модели,
энергетические инварианты (мощность, потери),
условия симметрии.
Это L2-формализм: векторные пространства, линейность, метрики, нормы, квадраты.
4.2. В L3 базовый объект — состояние из P3 и операция ⊙
Если я утверждаю L3, то я обязан предъявить:
P3 = {p0,p1,p2},
бинарную операцию ⊙ на P3,
инварианты и правила допустимых перенумераций Sym3/Z3,
и далее — локальную структуру, если это поле/ток/ремонт на носителе.
В трёхфазке нет встроенной операции ⊙ на трёх состояниях, потому что “фазы” — не состояния, а каналы одной и той же непрерывной величины, разнесённые по времени/пространству.
5. Нулевая последовательность и нейтраль: “третье” появляется как дефект/условие, а не как полюс
Есть распространённая ошибка: “ну вот же, три провода, нейтраль, нулевая последовательность — значит трехполярность”.
Нет. Нейтраль и нулевая последовательность — это именно демонстрация того, что:
“три” раскладывается на (2D полезная часть) + (1D нулевая часть),
и третья компонента появляется как канал дефекта/несимметрии, а не как третий полюс L3.
В языке представлений это стандартная картинка:
у S3 есть тривиальное представление (сумма компонент) и двумерное стандартное представление,
симметричная трёхфазка живёт в стандартном 2D,
а “нулевая последовательность” — это тривиальная компонента, которая включается при небалансе/особых соединениях.
То есть трёхфазка сама показывает, что “три” — это часто 2 + 1, где “1” — не третий полюс онтологии, а отдельный режим согласования/нарушения.
6. Почему это принципиально: “локальный ремонт” в трёхфазке — числовой, а в L3 — структурный
Теперь я связываю это с моим любимым (в целях создания разумного ИИ) ключевым требованием: “почему триада даёт локальный ремонт, а пара — нет”.
6.1. В трёхфазке ремонт — это перераспределение амплитуд/фаз (L2)
В реальности “ремонт” трёхфазной системы делается так:
перераспределением нагрузок,
компенсацией реактивной мощности,
балансировкой фаз,
фильтрацией гармоник,
переключением схем соединения.
Всё это — операции над непрерывными величинами и их линейными инвариантами.
6.2. В L3 ремонт — это переназначение состояния через третью полярность при сохранении инвариантов ⊙
В строгой L3 “ремонт” означает:
конфликт между двумя полярностями локально переводится в третью полярность,
затем возвращается в согласованное состояние,
при этом симметрии и инварианты таблицы ⊙ остаются валидны.
Это другой тип ремонта: не баланс амплитуд, а перестройка дискретного состояния при удержании закона отношений.
7. Итог главы 2 в одном тезисе (и почему это важно для статьи)
Трёхфазка содержит Z3 и действительно “любит триаду”, но:
в симметричном режиме она редуцируется к двумерному (L2) представлению,
а “третья компонента” возникает как нулевая последовательность/дефектный канал,
поэтому трёхфазка по строгому определению — это L2-физика с симметрией Z3, а не L3-онтология.
Чтобы получить строгую трёхполярность, нужно другое: состояние в P3 и операция ⊙, а также локальные правила ремонта/согласования на носителе, которые не сводятся к линейной балансировке.
Глава 3. Строгий тест на L3: что должно быть задано, чтобы “три” стало трёхполярностью, и почему трёхфазка этому не удовлетворяет
В главе 2 я показал центральную редукцию: симметричная трёхфазка в рабочем режиме живёт в двумерном представлении (alpha-beta), а “третье” всплывает как нулевая последовательность/дефектный канал. Теперь я формализую то, что обычно оставляют на уровне интуиций: по каким критериям система является строго L3, и как в моей дисциплине выглядят трёхполярное поле и трёхполярный ток — так, чтобы разница с трёхфазкой читалась сразу, без “философии”.
1) Тест на L3: три условия, без которых “тройка” остаётся L2 с Z3
Я считаю систему строго трёхполярной (L3) только если выполнены все три условия.
Условие L3-1. Онтология: задано множество полярностей P3
Должно быть явно задано:
P3 := {p0, p1, p2},
где p0, p1, p2 — не координаты, не “каналы измерения”, не “фазы во времени”, а первичные состояния.
Это ключевой водораздел: в трёхфазке “a,b,c” — это координатные компоненты (или проводники/обмотки), а не состояния.
Условие L3-2. Алгебра: задан закон отношений ⊙ на P3
Должна быть задана бинарная операция:
⊙ : P3 x P3 -> P3,
заданная полностью (таблицей/правилом). И главное — эта операция является смысловым законом взаимодействия (а не удобным переобозначением).
Это означает: когда я “склеиваю” два локальных состояния, результатом является одно из трёх состояний. В трёхфазке нет такой операции: сумма токов, сдвиг фаз, наложение сигналов дают непрерывный результат в R или C, а не элемент P3.
Условие L3-3. Локальность и ремонт: триада должна решать локальный конфликт
Нужно явное правило локального ремонта, которое не редуцируется к балансировке амплитуд:
для пары (p_i, p_j) должен существовать “ремонтный” выход в p_k,
и этот ремонт должен быть воспроизводимым, протоколируемым и инвариантным относительно допустимых перенумераций.
Формально: должен существовать предикат Repair3, который, получив конфликт пары, возвращает третью полярность (или её форму), сохраняя инварианты.
В трёхфазке “ремонт” делается как регулировка величин: перераспределение мощности, компенсация реактивности, настройка регуляторов. Это L2-ремонт; он не требует трёхполярной операции ⊙.
Вывод теста: если “три” живёт как три координаты непрерывного вектора и не имеет закона ⊙ на P3, то это не L3, даже при наличии Z3-симметрии.
2) Что такое трёхполярное поле в строгом смысле
Теперь я даю “точное” определение в моём стиле (с теми же дисциплинами, что у L4: объект, носитель, инварианты, локальность).
2.1. Определение: трёхполярное поле
Трёхполярное поле — это отображение состояния на носителе, принимающее значения в P3, с заданным законом локальной композиции ⊙ и с допустимыми перенумерациями Sym3/Z3, которые ковариантны закону.
Минимальная формальная версия:
дан носитель (граф/решётка/комплекс) с локальной структурой смежности;
поле:
Phi: Cells -> P3,
где Cells — набор локальных ячеек/элементов носителя;
задана операция ⊙ на P3;
определены допустимые симметрии g ∈ Sym3 (или хотя бы Z3), и выполнено:
g(Phi(x) ⊙ Phi(y)) = (g Phi(x)) ⊙ (g Phi(y)).
Смысл: симметрия — не “красота”, а закон допустимых перенумераций, не меняющий вычислимую структуру взаимодействия.
2.2. Где появляется локальность
Чтобы поле было “полем”, а не набором меток, должна быть определена локальная процедура, которая связывает соседние состояния:
либо через локальные ограничения (constraints) на тройки/циклы,
либо через локальный оператор “границы/контура” (в духе клеточного комплекса),
либо через ремонтный механизм.
Я подчёркиваю: L3 не обязано быть линейным. L3 в строгом смысле — это алгебра состояний, а не векторное пространство. Если я “усредняю” и получаю непрерывные величины — это уже проекция в L2.
3) Что такое трёхполярный ток в строгом смысле
Слово “ток” здесь важно не путать с электрическим током I(t) в амперах. Я определяю “ток” как направленную локальную передачу состояния/дефекта в L3-логике.
3.1. Определение: трёхполярный ток
Трёхполярный ток — это ориентированное распределение на рёбрах носителя, принимающее значения в P3 (или в производном множестве событий), согласованное с локальным законом сохранения/замыкания, выраженным через ⊙.
Минимальная версия:
на ориентированных рёбрах e задан:
J3: Edges -> P3,
или более строго: J3(e) ∈ Events3, где Events3 типизированы полярностями;
существует локальное правило “баланса” в вершине v, которое выражается как композиция входящих/выходящих полярностей по ⊙ даёт нейтральный элемент (или фиксированный класс допустимости):
⊙{e in In(v)} J3(e) ⊙ ⊙{e in Out(v)} Inv(J3(e)) = p0,
где Inv — заданная инволюция/обращение в L3 (если оно предусмотрено), либо иной канонический механизм замыкания.
Ключ: закон замыкания здесь не линейный “сумма токов = 0”, а закон композиции полярностей ⊙.
3.2. Почему трёхфазка не является трёхполярным током
В трёхфазке ток — это физическая непрерывная величина I(t) в каждом проводнике/фазе. Узловой закон Кирхгофа:
i_a + i_b + i_c (+ i_n) = 0
— это линейная аддитивность в R. Это чистая L2-структура.
Даже если я в трёхфазке вижу Z3 (перестановки фаз) и поворот на 120°, базовый объект остаётся вектором непрерывных компонент, а не элементом P3. Следовательно, “ток” трёхфазки — это L2-ток с Z3-инвариантностью, но не L3-ток.
4) Главный пункт “почему триада даёт локальный ремонт, а пара — нет” (в строгом виде)
4.1. Пара в L2 даёт только величину, но не даёт третьего состояния
Если у меня есть только L2-пара знаков/полюсов, конфликт “+/-” ремонтируется либо:
уничтожением (аннигиляцией),
подавлением амплитуды,
усреднением,
или переносом в “внешний канал” (ввод дополнительных переменных).
Это ремонт через числовую регуляцию, а не через структурное состояние.
4.2. Триада в L3 даёт третий смысловой исход, который закрывает конфликт локально
Если задана тройка P3 и таблица ⊙, то конфликт между двумя полярностями может иметь канонический третий исход — не как “среднее значение”, а как новое состояние, которое:
совместимо с симметриями (перенумерациями),
проходит локальные ограничения,
и может быть обратно развернуто (или стабилизировано) без внешней склейки.
Именно поэтому я говорю: триада даёт локальный ремонт, если и только если в системе реально задана L3-алгебра состояний.
Трёхфазка “чинится” не так. Она чинится как L2-система: балансом, фильтрами, регуляторами, преобразованием координат. Это инженерно великолепно, но это не L3-онтология.
5) Инженерный чек-лист: как за 60 секунд отличить “трёхфазку” от “трёхполярности”
Чтобы это было практично, вот проверка “на бумажке”.
Если это трёхфазка (L2 с Z3), то верно:
можно перейти к (alpha, beta, 0) и увидеть редукцию в 2D при балансе;
закон узла — линейный: сумма токов/напряжений;
существует естественный комплексный фазор как упаковка 2D;
ремонт — регулировка величин (баланс/компенсация/фильтрация).
Если это строгая L3, то обязано быть:
P3 = {p0,p1,p2} как первичные состояния;
операция ⊙: P3xP3->P3 (таблица/правило);
локальный закон замыкания/сохранения через ⊙ (а не через сумму);
Repair3: правило локального ремонта “пара -> третий” без ухода в непрерывную компенсацию.
Если этих четырёх пунктов нет — это не L3.
6) Итог главы 3
Трёхфазная система действительно несёт Z3-симметрию (поворот 120° и перестановки фаз), но эта симметрия действует на координаты непрерывных величин и в рабочем режиме приводит к двумерной редукции (alpha-beta). Поэтому трёхфазка — это L2-физика с Z3-симметрией, а не строгая трёхполярность.
Строгая L3 требует другого типа объекта: трёхсостоянийного поля и трёхполярного тока, заданных через P3 и закон ⊙, где триада является не “три канала”, а “три состояния с собственным законом локального ремонта”.
Заключение
Я подвожу итог так: трёхфазная система переменного тока не является строгой трёхполярностью, потому что она реализует не Z3-алфавит состояний, а три временно сдвинутые копии одного и того же двухполярного измерительного канала.
Почему “три провода” в трёхфазке не делают её L3. В сбалансированном режиме три фазных тока имеют вид
I_a(t) = I0 cos(omega t) I_b(t) = I0 cos(omega t - 2pi/3) I_c(t) = I0 cos(omega t + 2pi/3)
и связаны ограничением
I_a(t) + I_b(t) + I_c(t) = 0 .
Это означает, что в каждый момент времени существует только две независимые степени свободы: третья восстанавливается из суммы. Поэтому “три фазы” в классической трёхфазке — это не три независимые полярности, а избыточное представление двухмерного измерительного объекта (что и проявляется в стандартных преобразованиях к двухкомпонентному представлению типа α–β). Следовательно, трёхфазка по своей математической сути остаётся L2-конструкцией, даже если инженерно она разведена на три жилы.
Что я называю строгим трёхполярным током. Строгая трёхполярность для меня — это ситуация, когда ток несёт дискретную метку из тройки, и допустимая симметрия — это циклическая перенумерация:
A -> B -> C -> A
то есть действие Z3 (поворот на 120° как операциональный смысл). В таком токе принципиально важно, что переносится не “три синуса”, а элемент алфавита состояния. Именно поэтому я в статье настаиваю на различении:
электрический ток в проводнике как L2-наблюдаемая величина (скалярный канал с инволюцией знака в измерениях), и
трёхполярный ток как ток трёхполярного состояния (перенос/переключение Z3-метки на носителе).
В этом смысле трёхполярный ток ближе по логике не к “передаче мощности”, а к переносу доменного/подрешёточного/модового индекса, который может иметь электрические проявления, но не обязан сводиться к ним.
Нужно ли для L3 “строго три провода”. Я фиксирую следующее: утверждение “трёхполярный ток движется строго по трём проводам” — слишком жёсткое в физическом смысле.
Инженерно три отдельных проводника — это самый простой способ реализовать три канала, которые не смешиваются “по умолчанию”. В этом смысле “три провода” являются удобным (и часто единственным практичным) способом разведения каналов.
Структурно же трёхполярность задаётся не количеством жил, а тем, что у носителя есть три устойчивых различимых состояния и допустимые операции их циклически переставляют. Поэтому трёхполярный ток может быть реализован и в одном физическом теле, если внутри него существуют три внутренние подсистемы/моды, которые ведут себя как Z3-алфавит.
Именно так я снимаю ложную связку “полярность = число проводов”: в моей дисциплине полярность — это внутренний алфавит состояния носителя, а провод — лишь геометрия и технология разведения каналов.
Разберем предполагаемые L3-проводники:
(а) Тримеризованные гексагональные манганиты как Z3-носитель доменной метки. В гексагональных манганитах (типичные примеры: YMnO3, ErMnO3) структурная тримеризация даёт вырождение, описываемое как разрыв Z3, а полярное искажение добавляет Z2, что совместно приводит к Z6-доменной структуре и устойчивым топологическим дефектам. Это ровно тот класс систем, где Z3-метка не является “рисунком”, а является строгим состоянием носителя, допускающим топологически защищённые доменные конфигурации. В таких средах я трактую кандидат трёхполярного тока так: перенос/дрейф доменных границ и переключение тримеризационной метки является переносом Z3-информации, причём электрическая проводимость может локализоваться на доменных стенках (что делает связь с измерительным L2-каналом операциональной, а не риторической) (Nature).
(б) Минерал молибденит (MoS2) и родственные слоистые халькогениды как носители “тройки эквивалентных мод” при повороте на 120°. Это пример того, как в одном кристалле возникает тройка эквивалентных состояний, связанных поворотами на 120°, то есть появляется естественный кандидат на Z3-индекс (внутренний “канал”, отличимый структурно). В работах по монолайерным дихалькогенидам переходных металлов (MoS2 и др.) обсуждаются эквивалентные точки/минимумы зоны проводимости, связанные симметрией решётки под поворотами на 120°, и соответствующие кратности вырождения (Biblos-e Archive). В таком классе носителей я считаю принципиально возможным режим, где перенос заряда сопровождается переносом трёхзначной модовой метки (по сути — “какой из трёх эквивалентных каналов занят/возмущён”), то есть появляется содержательное приближение к трёхполярному току внутри одного тела, без трёх проводов как обязательного условия.
(в) Z3-упорядочения типа “Z3 charge density wave” как прямой прототип трёхполярной метки в одном носителе. Существуют экспериментально обсуждаемые системы, где коллективное электронно-структурное упорядочение имеет Z3-характер (в частности, в работах по атомным цепочкам кремния на поверхности Si(111) прямо вводится Z3-зарядово-плотностное упорядочение) (ResearchGate). Ток трёхполярного типа здесь естественно трактуется как перенос/переключение Z3-фазы/метки упорядочения (а не как сумма трёх синусов в трёх жилах).
Отсюда я делаю прямой, утвердительный вывод: строгий трёхполярный ток не обязан “идти по трём проводам”, но обязан иметь три независимых структурных состояния, и потому в обычной металлической проволоке, где носитель по умолчанию L2-типа, он не реализуется как строгий объект.
Читайте также: