Как решить гаальскую икебану
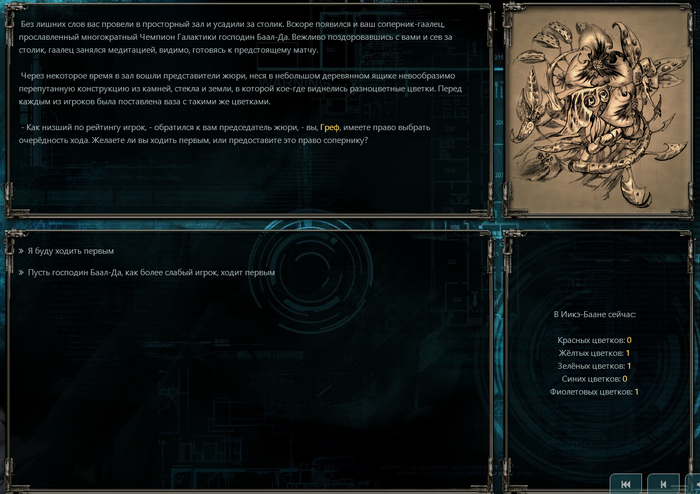
Для тех, кто читал Гарднера, квест «Иикэ-баана» из «Космических рейнджеров» очень прост. Я решил и забыл, но много лет спустя вынужден был снова исследовать этот квест — просто потому, что за ним лежит кое-какая математика. (Извините, что привожу скриншот из онлайн-плеера, а не живой игры.)
Правила игры.
В полной иикэ-баане 15 цветков — по три красных, зелёных, синих, фиолетовых и жёлтых (эти цвета символизируют пять рас Коалиции; люди, если что, синие).
Игрок кладёт в иикэ-баану один, два или три цветка одного цвета — но так, чтобы суммарно с имеющимися всё равно не превышало три.
Выигрывает тот, кто дополнит иикэ-баану до полной.
Кто начинает — выбираем мы. Соперник играет идеально, и если дашь слабину, он выигрывает.
Исходная ситуация случайная: вот что делать, если попалось 0-0-0-1-3?
Большинство авторов пишут какие-то сложные таблицы. А ведь стратегия простая и легко запоминающаяся.
Ответ для Лиги лени
Вычёркиваем цифры 3, а также пары одинаковых.
Ничего не осталось: ситуация проигранная, отдаём ход сопернику.
Остался один цвет: дополняем его до 3.
Остались два цвета: дополняем меньший до большего.
Остались три цвета 0, 1 и 2 — ситуация проигранная, отдаём ход сопернику.
Если можно повторить ход соперника (например, дополнить 0 до 2) — делаем это!
В нашей ситуации 0-0-0-1-3 вычёркиваем 3 и 0-0, и получаем 0-1, два цвета. Наш ход — дополнить 0 до 1.
Ним
Корявое «чтобы суммарно с имеющимися не превышало три» уже говорит, что иикэ-баана сделана из какой-то известной математической игры, где мы не докладываем цветы, а убираем предметы из кучек. Эта игра называется ним.
Есть N кучек. Игрок может убрать сколько угодно предметов из любой кучки. Выигрывает тот, кто заберёт последний.
Так что наша иикэ-баана — это перелицованный ним: позиция 0-0-0-1-3 иикэ-бааны соответствует позиции 3+3+3+2+0 нима. Ну или 3+3+3+2 — нулевые кучки не играют роли. В дальнейшем будем работать именно с нимом, и чтобы отличать ним от иикэ-бааны, в нём будут плюсы.
Немного определений
Игра называется беспристрастной, если у обоих игроков один и тот же набор действий, с одинаковыми результатами.
Игра называется игрой до последнего хода, если любая партия конечна, и проигрывает тот, у кого не осталось ходов.
Ним относится и к тем, и к другим. Будем писать БИдПХ — беспристрастная игра до последнего хода.
Если в БИдПХ в проигранной ситуации отдать ход сопернику, соперник сам будет в проигранной ситуации. Другими словами, там нет ситуаций «выигрывают белые» и «выигрывают чёрные», есть «выигрывает первый» и «выигрывает второй». А вот кто выигрывает — за это отвечает любопытная функция.
Любая БИдПХ обладает функцией Шпрага-Гранди (ФШГ), которая определяется просто: для ситуаций, когда некуда ходить, она равна 0. У нас такая ситуация одна (не осталось ни одного предмета), то есть F(0) = 0. А если есть куда ходить — перебираем все производные позиции, и находим самое маленькое число, которого нет среди них.
Другими словами, у позиции 1 единственная производная 0, чья ФШГ равна 0. А наименьшее отсутствующее — понятно, 1. У позиции 2 производные 0 и 1, а наименьшее отсутствующее — 2. И так далее. Так что заметим: F(n)=n.
ФШГ равна нулю, если все производные позиции имеют ненулевую ФШГ. А те ненулевые, потому что хоть одна производная позиция нулевая. Получаем чеканное правило:
Если ФШГ равняется нулю — позиция проигранная.
А если нет — оставляем сопернику нулевую позицию.
ФШГ нима
Пока мы работали с одной кучкой — ежу понятно, что она всегда выигрышная. Добавим вторую и выясним, чему равняется F(m+n).
F(1+1) = 0, ведь это явно проигранная позиция: ты берёшь один предмет, соперник второй.
Теперь посмотрим, чему равняется F(2+1): можно получить 2+0 (F=2), 0+1 (F=1) и 1+1 (F=0). Первый отсутствующий — 3. Итого F(2+1)=3.
Считаем F(3+1): F(3+0)=3, F(2+1)=3, F(1+1)=0, F(0+1)=1. Первый отсутствующий — 2. Итого F(3+1)=2.
Дальше F(4+1)=5, F(5+1)=4, F(6+1)=7, F(7+1)=6 (можете посчитать сами). Компьютéрик уже в предвкушении потирает руки. F(2+2)=0, F(3+2)=1, F(4+2)=6!!, F(5+2)=7, и почему-то F(6+2)=4. Компьютéрик говорит: да, оно!
Раскрою, что это за компьютерная функция — побитовое исключающее ИЛИ. Устроено оно так: допустим, нам надо вычислить 5⊕3 — переводим их в двоичную систему, 101₂⊕011₂. А теперь поразрядно складываем эти двоичные числа, отбрасывая перенос: 1+0=1, 0+1=1, 1+1=10₂, но мы условились не переносить в высшие разряды, и 1⊕1=0. Итого 5⊕3=101₂⊕011₂=110₂=6.
Теорема. F(m+n)=m⊕n.
Очень нестрогое доказательство. Нам нужно доказать два факта.
Любое меньшее число получить можно.
А m⊕n нельзя.
Начнём со второго пункта. Допустим, мы вытянули что-то из кучки m так, что осталось p<m, и p⊕n=m⊕n. «Прибавив» к обеим частям n и воспользовавшись тождеством n⊕n=0, получаем p⊕n⊕n=m⊕n⊕n, или p=m. Противоречие.
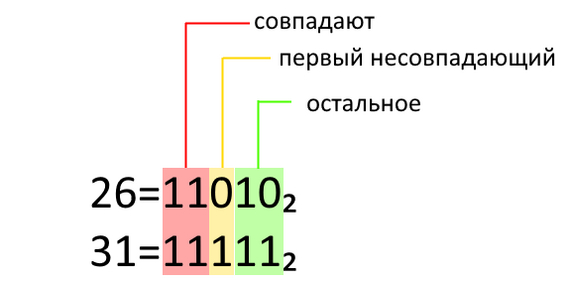
Теперь первый пункт. Допустим, что m=26 и n=31; 26⊕31=5. Делим их двоичную запись на три участка.
Если урезать 26 или 31 настолько, что перещёлкнется один из красных разрядов — например, 26 и 19=10011₂ — в сумме 26⊕19=9 появится разряд 2³=8. Так меньшего не добьёмся.
А меньшего можно добиться, занулив в числе 31 жёлтый разряд. Зелёные разряды могут быть какие угодно, и любых сумм от 0 до 3 мы точно добьёмся.
Если менять только зелёные разряды — возможна ситуация и красная, и жёлтая. Задев второй разряд (например, превратив 26 в 25=11001₂), мы получим 6 или 7, что тоже больше 5. А вот превратив 31 в 30=11110₂, получим 4, которого нам не хватало.
На самом деле теорема верна для любого N кучек. Как расширить — оставляю домашним заданием.
Побитовое исключающее ИЛИ даже получило особое название в математике — ним-сумма.
Стратегия
Считать в уме ним-сумму не любит даже компьютéрик. Но у нас много кучек и мало предметов, и потому можно подключить два тождества: x⊕x=0; x⊕0=x. Первое — это правило «вычеркнуть одинаковые», второе — «вычеркнуть тройки» (напомним, 3 цветка в иикэ-баане — это 0 предметов в ниме). А для того, что осталось, придумываем умные рекомендации.
Наконец, откуда правило «повторяй ход соперника». Пусть у нас есть две одинаковых кучки, и соперник урезал одну из них x→y. Поскольку и x⊕x=0, и y⊕y=0, то имеет место тождество x⊕x⊕a⊕…=y⊕y⊕a⊕… Вот и всё.


Уголок ретрогеймера
4.1K постов13.4K подписчиков
Правила сообщества
Регистрационный номер: № 5416719577
Правила сообщества:
1. Игры вне религии и политики
2. Уважайте игровые предпочтения других пользователей
3. Любые оскорбления других пользователей запрещены
4. Пустые и бессмысленные посты запрещены и кидаются в общую ленту
5. Игры, которые не относятся к категории ретро будут переносится в Лигу Геймеров или общую ленту Пикабу
6. Реклама любой продукции и сервисов без согласования запрещена
7. Любой поиск игр происходит в Лиге Потерянных Игр:
9. Все договоренности игры по сети происходят в сообществе Онлайн ретро-игр: