С понятием «несколько» мы сталкиваемся ежедневно и повсеместно, но его метрические (количественные) свойства не определены. Для примера зададим вынесенный в заголовок вопрос самому себе, своим знакомым и получим очень интересные результаты. Так, например, на вопрос ««несколько» - это сколько?», мы почти наверняка получим ответ, что «несколько» лежит в диапазоне [(2 - 3), (10 - 15)], т.е. нижняя граница интервала лежит на отметке 2 или 3, а верхняя на отметках от 10 до 15.
Если задать этот же вопрос в несколько другой форме: ««несколько сот» - это сколько?», мы с удивлением обнаружим, что верхняя граница интервала значительно сместиться вниз и ответ будет: [(2 - 3), (6 - 7)].
Если ещё более усугубить вопрос и задать его в следующей форме: ««несколько тысяч» - это сколько?», то верхняя граница интервала сместиться ещё больше и ответ будет выглядеть так: [(2 - 3), (4 - 5)].
Пойдём дальше и зададим вопрос: ««несколько миллионов» - это сколько?» и вопреки ожиданиям верхняя граница интервала в ответах сместиться в большую сторону и ответ будет примерно такой: [(2 - 3), (5 - 6)]. Пока не будем останавливаться на этом феномене в определении верхней границы интервала, а зададимся вопросом: Можно ли математически точно определить интервал для понятия «несколько»?
Для начала отметим, что понятие «несколько» применяется к величинам, имеющим очень большой разброс по абсолютной величине. Это могут быть единицы, десятки, тысячи, миллионы штук, или метры, километры, килограммы, тонны. Это могут быть и дробные величины, такие как сантиметры, миллиметры, литры, миллилитры, граммы, миллиграммы и т. д. Поскольку мы пользуемся позиционной системой счисления, то порядок величины может быть вынесен за скобки рассмотрения и служить простым размерным множителем для того отрезка, который мы оцениваем как «несколько». В этом случае удобно воспользоваться логарифмическими представлениями, т. е. использовать логарифмическую шкалу для представления величин. С учётом сказанного, приведём все величины к единому интервалу, базовую величину которого выберем равной основанию (M) используемой позиционной системы счисления. В привычной для нас десятичной системе счисления длина базового интервала будет равна 10 единицам. Он и будет служить нам осью х (смотри рисунок).
Отметим, что в начале оси стоит не 0, а 1, а в конце оси 10, но ось при необходимости может быть продолжена и за эту отметку. К данному интервалу может быть применён любой масштабный коэффициент, это не меняет сути этого интервала и свойств отложенных на нем величин. Например, в системе СИ, если масштабный коэффициент имеет значение 100 - то это могут быть метры, тогда 10-3 - миллиметры, 103 - километры, 10-10 - ангстремы, или если 100 - кубические метры, тогда 10-3 - литры, 10-2 - декалитры, 10-6 - миллилитры и т.д. В результате всё сопоставление будет вестись в пределах единого базового интервала, равного основанию системы счисления.
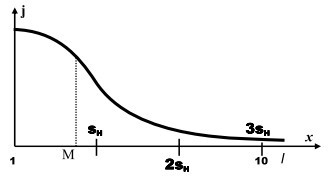
С другой стороны, поскольку понятие «несколько» используется очень широко и в различных контекстах, то можно ожидать, что оно, как случайная величина, должно иметь нормальный закон распределения. Отметим также, что данное понятие не чувствительно к знаку, и мы вправе считать, что оно одинаково применимо как к тому, что идёт со знаком «плюс», так и к тому, что оценивается со знаком «минус». Поэтому в нашем случае будет правомерным взять в качестве функции распределения случайной величины «несколько» распределение модуля случайной величины, распределённой по нормальному закону [Справочник по вероятностным расчётам, М.: Воениздат, 1970, с.85 - 87]. Данное распределение характеризуется двумя параметрами: центром рассеяния (х0) и средним квадратичным отклонением (sн). Для нашего случая зададим эти величины равными х0 = 1, sн = 3, тогда функция плотности вероятности (j) будет иметь вид, показанный на рисунке. Её математическое ожидание (MO) равно 0,798sн = 2,39, дисперсия равна 0,3634(sн)2 = 3,270, s = 0,6028sн = 1,808. В результате, переходя на базовом интервале от логарифмического масштаба (log(M)) к линейному, получим, что математическое ожидание понятие «несколько» близко к 2 (100,239 = 1,7), а согласно «правилу двух сигм» в 95% случаев понятие «несколько» не превысит величину, равную 4 (100,239+0,362 = 3,99). Таким образом, понятие «несколько» лежит в диапазоне от 2 до 4.
Теперь рассмотрим отмеченный выше феномен с инверсией направления изменения верхней границы интервала «несколько» при переходе к миллиону. Человек практически ежедневно и широко пользуется деньгами для покупки товаров и услуг. Наиболее часто он пользуется такими единицами как рубли, десятки и сотни рублей, реже тысячами. Количество людей, пользующихся в своей повседневной практике десятками тысяч рублей и более достаточно мало. Тогда можно проследить следующую тенденцию. Чем выше повседневная потребительская значимость денежной купюры для человека, тем ближе для неё устанавливаются границы значения «несколько» к их математически точному значению. Поскольку миллион для обычного потребителя не является повседневной купюрой, то его повседневная потребительская значимость для человека более абстракция, чем реальность. В этом случаи и границы понятия «несколько» для миллиона устанавливаются скорее как для абстрактного, чем реального объекта, поэтому и оказываются завышенными. А мы-то считали, что ведём опрос на отвлечённых, абстрактных числах и понятиях, а всё свелось подспудно к обыденным денежным знакам, с которыми мы оперируем повседневно. Это следует учитывать при проведении опросов и, особенно, при интерпретации полученных результатов.
Приведённые выше рассуждения о границах понятия «несколько» можно применить к позиционным системам счисления с произвольным основанием. Воспользуемся широко распространённой в вычислительной технике 16-ричной системой счисления. В этом случае длина базового интервала будет равна 16 единицам (от 1 до 16) и поэтому в рассуждениях необходимо использовать логарифмические представления так же по основанию 16. Для функции распределения исходными параметрами будут х0 = 1, sн = 5, тогда математическое ожидание величины «несколько» равно 0,7979sн = 3,9895; дисперсия равна 0,3634(sн)2 = 9,0850; s = 0,6028sн = 3,0140. При переходе от логарифмического к обычному представлению (не забудем, что логарифм берётся по основанию 16), ответ на поставленный в заголовке материала вопрос будет следующим: понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6. Для системы счисления по основанию 8 (ещё одна система счисления, применяемая в вычислительной технике) получим следующий ответ: от 2 до 3.
Таким образом, можно сказать, что понятие «несколько» для:
16-ричной системы счисления лежит в диапазоне от 2 до 6;
10-тичной системы счисления в диапазоне от 2 до 4;
8-ричной системы счисления - от 2 до 3.
Журнал "Современные наукоемкие технологии" 2009. №4
https://www.top-technologies.ru/ru/article/view?id=26312