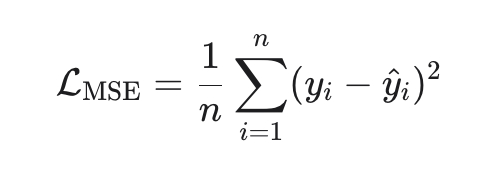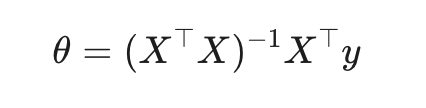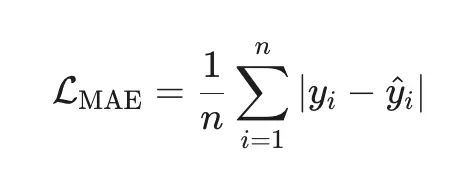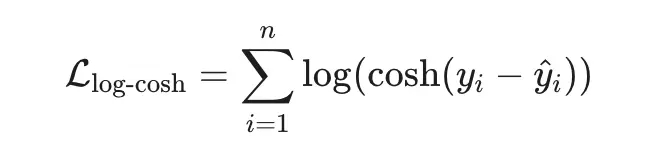Мне сегодня 7 годиков! (^o^)1
В честь ДР ловите мой музыкальный ремикс клипа из поста Ответ на пост «Функции потерь и алгоритмы оптимизации в линейной регрессии: обзор основных подходов» в сообществе Наука | Научпоп
Объясню, откуда в клипе взялись иностранные языки)
В конце прошлой и начале этой неделе взлетел мой Инстаграм (ссылку не дам), менее чем за неделю вырос с 200 подписчиков до 2200. Начал делать клиповый курс «Что такое...», где за 20 секунд объясняю термины из машинного обучения и разработки нейросетей. За неделю в Instagram набрал 1,7 млн просмотров, топовый рилс про Оптимизатор Adam (второй в посте по ссылке выше) забрал половину из них - 825к просмотров. Лайки, шэры, репосты и сохранения в избранное там бьют рекорды, с них и завирусился мой контент.
Клипы делаю на русском, но теперь добавляю ещё английский и испанский переводы в комментариях или субтитрах, т.к. Инстаграм очень активно рекомендует мои рилсы в т.ч. иноязычной аудитории.
Футажи от Wan, голосовой движок Google TTS.
Ответ на пост «Функции потерь и алгоритмы оптимизации в линейной регрессии: обзор основных подходов»1
Что такое функция потерь?
Что такое оптимизатор Adam?
Делаю такой клиповый курс «Что такое», где за 20 секунд объясняю термины по разработке нейросетей и искусственному интеллекту.
Если пост наберёт 30 плюсов, продолжу выкладывать другие клипы в сообществе «Наука | Научпоп».
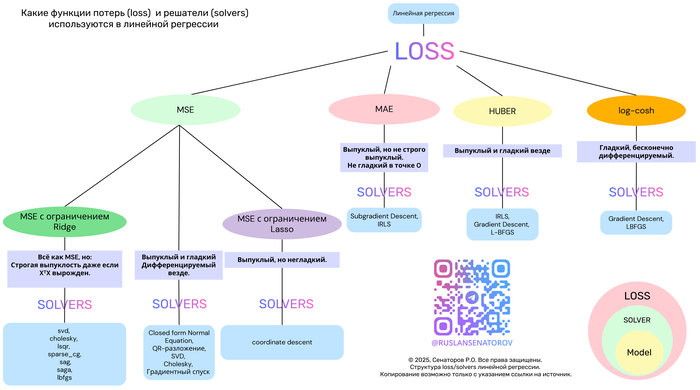
Функции потерь и алгоритмы оптимизации в линейной регрессии: обзор основных подходов1
Линейная регрессия — один из самых фундаментальных и широко применяемых методов в машинном обучении. Несмотря на простоту, её эффективность сильно зависит от двух ключевых компонентов:
Функции потерь (loss function) — что именно мы минимизируем?
Метода оптимизации (solver) — как мы ищем решение?
В этой статье мы разберём популярные функции потерь — MSE, MAE, Huber и Log-Cosh — их свойства, плюсы и минусы. А также покажем, как выбор функции потерь определяет выбор алгоритма оптимизации.
Почему функция потерь так важна?
Функция потерь измеряет, насколько предсказания модели отличаются от реальных значений. От её формы зависят:
Чувствительность к выбросам
Наличие замкнутого решения
Выпуклость задачи
Скорость и стабильность обучения
Давайте сравним четыре ключевые функции потерь в контексте линейной регрессии.
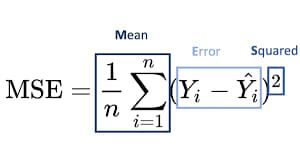
1. MSE (Mean Squared Error) — стандарт по умолчанию
Эквивалентна максимуму правдоподобия при нормальном шуме.
Замкнутое решение (метод наименьших квадратов):
Плюсы:
Выпуклая, гладкая, дифференцируемая → легко оптимизировать
Минусы:
Чувствительна к выбросам (ошибки возводятся в квадрат).
Solver:
Normal Equation (аналитическое решение)
SGD, SAG, LBFGS (в scikit-learn: solver='auto', 'svd', 'cholesky' и др.)
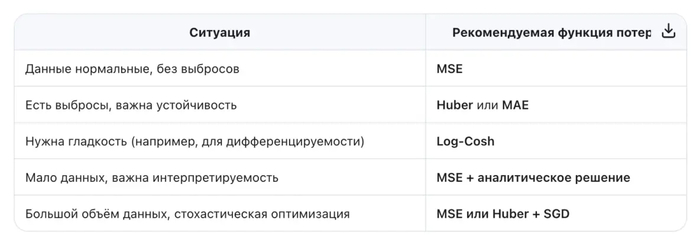
Когда использовать: когда данные «чистые», ошибки гауссовские, и важна интерпретируемость.
2. MAE (Mean Absolute Error) — робастная альтернатива
Плюсы:
Робастна к выбросам (ошибки в первой степени).
Минимизирует медиану ошибок (а не среднее).
Минусы:
Недифференцируема в нуле → нет аналитического решения.
Требует итеративных методов.
Solver:
Linear Programming (например, через симплекс-метод)
Subgradient Descent (в scikit-learn: QuantileRegressor с quantile=0.5)
Когда использовать: когда в данных есть аномалии или тяжёлые хвосты (например, цены, доходы).
3. Huber Loss — лучшее из двух миров
Плюсы:
Гладкая и дифференцируемая.
Робастна к выбросам (линейная штраф за большие ошибки).
Гибкость через параметр δδ.
Минусы:
Нужно настраивать δδ (часто выбирают как процентиль ошибок).
Нет замкнутого решения.
Solver:
Gradient Descent, LBFGS, Newton-CG(в scikit-learn: HuberRegressor с fit_intercept=True)
Когда использовать: когда вы подозреваете наличие выбросов, но хотите сохранить гладкость оптимизации.
4. Log-Cosh Loss — гладкая робастность
Плюсы:
Гладкая везде (бесконечно дифференцируема).
Ведёт себя как MSE при малых ошибках и как MAE при больших.
Устойчива к выбросам, но без «изломов».
Минусы:
Вычислительно дороже (логарифм и гиперболический косинус).
Не так распространена в классических библиотеках.
Solver:
Gradient-based методы: SGD, Adam, LBFGS(в TensorFlow/PyTorch легко реализуется; в scikit-learn — через кастомный регрессор)
Когда использовать:
когда вы ищете баланс между робастностью MSE и гладкостью MAE.
Вы хотите избежать чувствительности MSE к выбросам, но сохранить дифференцируемость.
Вы строите гибридную модель, где loss должен быть всюду гладким (например, для вторых производных).
Правило:
Если loss квадратичен → можно решить напрямую.
Если loss неквадратичен → нужен итеративный численный метод.
И помните: нет универсально «лучшей» функции потерь — только та, что лучше всего подходит вашим данным и задаче.
Как понять всё машинное обучение через линейную регрессию?
Сердце всех ML алгоритмов это функция потерь, научившись её оптимизировать мы поймём как обучаются машины.
Дальше в посте, я опишу свойства функции среднеквадратичной ошибки (MSE), затем методы её оптимизации (аналитические, численные, стохастические и гибридные), укажу важные формулы, поведение градиента/Гессиана, оценки сходимости и практические рекомендации.
Основные свойства MSE
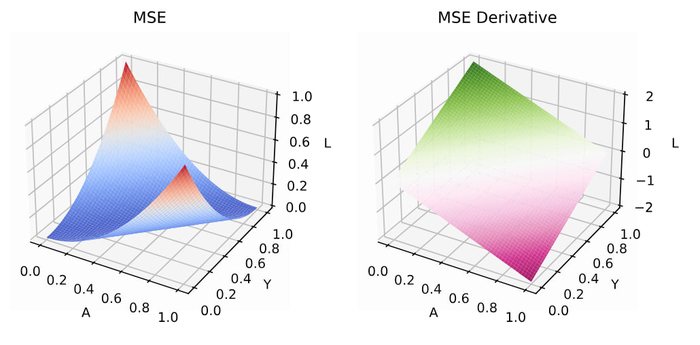
1. Дифференцируемость
MSE — гладкая (бесконечно дифференцируема) функция параметров для линейной модели она квадратичная — что сильно упрощает анализ.
2 Квадратичность и выпуклость
MSE — квадратичная функция, такая функция выпукла (всегда), а если X⊤X положительно определена (то есть признаки линейно независимы и строго выпукла и имеет единственный глобальный минимум.
Для нелинейных параметрических моделей выпуклость обычно не выполняется — могут быть локальные минимума.
3. Градиент и Гессиан
Гессиан положительно полуопределён. Его собственные значения управляют «кривизной» функции (вдоль направлений с большими э-величинами функция круто меняется).
4 Шкала, чувствительность к выбросам и статистическая интерпретация
MSE сильно чувствительна к выбросам (квадратичная зависимость даёт большим ошибкам непропорционально большой вклад).
Если ошибки в модели нормальны, то MSE (максимизация правдоподобия) соответствует MLE — минимизация MSE = максимизация нормального правдоподобия.
5. Аналитическое решение
Закрытая форма (normal equations).
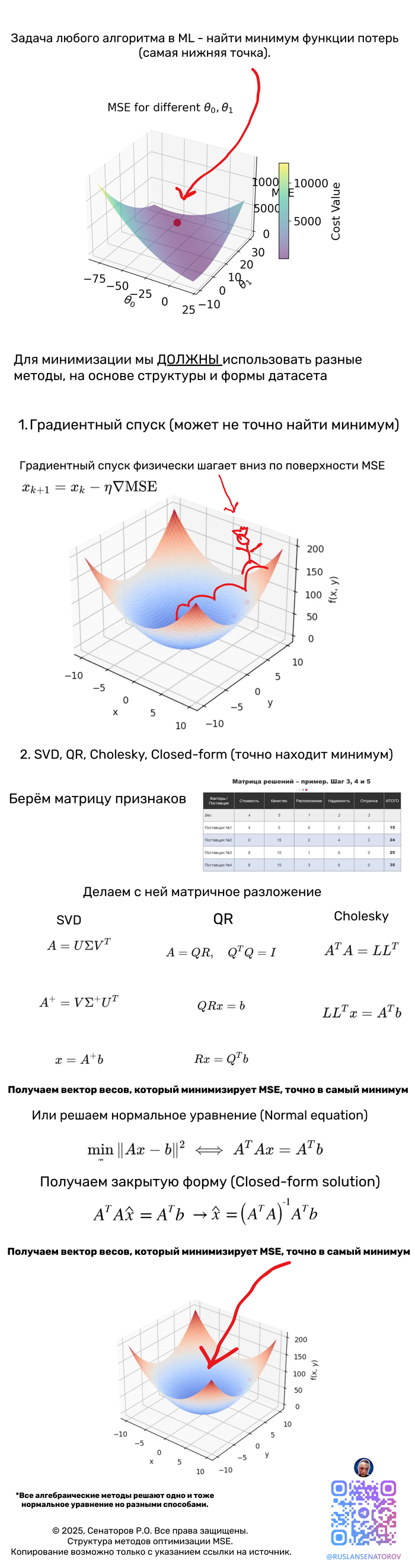
6. Алгоритмы численной оптимизации
Градиентный спуск (Batch Gradient Descent)
7. Стохастический градиентный спуск (SGD) и мини-батчи
Стохастичность даёт возможность выйти из плохих локальных минимумов (для нелинейных задач).
8. Ускоренные и адаптивные методы
Momentum (classical momentum) — ускоряет спуск по узким долинам.
Nesterov Accelerated Gradient (NAG) — улучшенный momentum с теоретическими гарантиями.
Адаптивные алгоритмы: Adagrad, RMSProp, Adam, AdamW. Они подбирают адаптивный шаг для каждого параметра.
9. Второго порядка и квазиньютоновские методы
Newton’s method (использует Гессиан) Kвазиньютоновские: BFGS, L-BFGS Conjugate Gradient (CG) часто используют для ridge регрессии
10. Проксимальные и координатные методы (для регуляризации)
Coordinate Descent — особенно эффективен для L1-регуляризованных задач (LASSO), когда функция частично сепарабельна.
11. Прямые методы оптимизации
SVD, cholesky, QR
Обратите внимание что в посте вы не увидите саму модель линейной регресии, где мы точки прямой аппроксимируем, потому что это вообще неинтересно с точки зрения понимания моделей машинного обучения, интересно только сердце ML моделей - функция потерь.
ViRush 2030
Я, Владислав, рассказывал на ViRush 2030 о том, как ArLift управляет 2000+ единицами техники в 22+ регионах с помощью Data-Driven подхода 🚀
Когда у тебя есть операции в Москве, Питере, Владивостоке и ещё 19+ регионах — ты не можешь позволить себе роскошь решать на интуиции. Главный вызов:
✅ Владивосток работает, Санкт-Петербург спит — а ты должен принимать решения круглосуточно
✅ 2000 единиц разной техники — каждая со своей спецификой, нужен единый стандарт анализа
✅ Отчеты идут 3-5 дней вместо того, чтобы быть моментально под рукой
✅ Данные раздроблены по 10+ источникам — нет единой картины бизнеса
Результат? CIO вынужден был выбирать: либо иметь быстрые решения, либо иметь достоверные данные.
И вот здесь вмешался управление данными как ключ к успеху.
🎯 О чем я с Анастасией говорили:
1️⃣ Оптимизация процессов
Вместо того, чтобы ждать 80% времени на сборку отчетов — Visiology свел это к нескольким часам. Автоматизация интеграции 10+ источников данных, и команда работает с анализом, а не с Excel 📊
2️⃣ Прозрачность данных — для всех 🔍
Когда в нескольких регионах случаются проблемы с техникой, руководитель видит это в реальном времени. Интуитивные дашборды Visiology — не для ИТ специалистов, а для всех сотрудников, от менеджера до директора.
3️⃣ Качество аналитики + быстрота решений ⚡
95% точность данных (ноль ручного ввода = ноль ошибок). Критичные сигналы идут не через СМС, а через систему — моментальное реагирование на алармы.
4️⃣ Масштабируемость без боли 📈
Модель работает одинаково, приходишь в новый регион — присоединяешь его к шине данных. Гибридное облачное+локальное решение = безопасность, гибкость, скорость.
🏆 Что получилось:
📌 80% экономия времени на подготовку показателей
📌 95% точность данных вместо ошибок вручную
📌 Еженедельные дашборды вместо месячных отчетов
📌 Единая корпоративная модель данных для всех 22+ регионов и 2000+ машин
Короче: не нужна суперсложная система — нужна система, которая работает как часы и дает ответы в момент, когда они нужны.
🔥 Главная идея:
CIO, который управляет данными как Visiology, становится не "блокером инфраструктуры", а стратегом, который держит руку на пульсе бизнеса. Пока конкуренты гадают — ты уже понял, где прибыль, где кровотечение, где возможность.
Управляйте данными — управляйте будущим!
На ViRush 2030 это было не про PowerBI vs Visiology, и не про облако vs локальное. Это было про то, что в эпоху ИИ компания без real-time аналитики будет отстающей. И CIO, который это понимает и внедряет, — уже выигрывает.
🎯 Хотели услышать нас? Следующий ViRush ждёт вас в 2026.
#ViRush2030 #CIOлогия #DataDriven #BusinessIntelligence #Аналитика
P.S. Всем CIO, кто ещё думает, сколько недель уходит на подготовку квартального отчета — вам срочно на ViRush 😎🚀
1 источник
Теперь подготовь большей развернутый пост на habr
5 шагов выполнено
[CIO] Как мы управляем 2000+ единицами техники в 22 регионах через единую аналитическую платформу
Владислав, CIO ArLift
На ViRush 2030 мы с коллегой Анастасией поделились кейсом, как трансформировать операционное управление в условиях географически распределенного бизнеса. В этом посте — детали внедрения, цифры и уроки, которые могут быть полезны CIO, CTO и руководителям digital-направлений.
Проблематика: почему старые подходы не работают
У ArLift 22+ региональных представительств от Владивостока до Санкт-Петербурга, более 2000 единиц разнородной техники и 10+ автономных IT-систем на периметре. Классическая модель управления — централизованный сбор отчетности, ручная консолидация в Excel, недельный цикл подготовки данных для принятия решений.
Ключевые боли до трансформации:
1. Время реакции
Отчет из регионов шел 3-5 дней. За это время ситуация успевала измениться. Владивосток работает, когда Питер спит — а управленческая команда не имела инструментов для круглосуточного мониторинга.
2. Раздробленность данных
Каждый регион использовал свои инструменты: 1С, Bitrix, разные CRM, Excel-файлы на сетевых дисках. Единой модели данных не существовало — каждый отчет был «истиной в последней инстанции» для своего владельца.
3. Качество и достоверность
Ручной ввод, копирование из системы в систему, отсутствие единых стандартов — ошибки достигали 15-20% в критичных показателях (загрузка техники, простои, доходность на единицу).
4. Масштабирование
При открытии нового представительства внедрение аналитики занимало 3-4 месяца. Каждый раз — заново настраивать коннекторы, дашборды, процессы.
5. Управленческая слепота
Руководитель не мог в моменте ответить: «Какая техника сейчас простаивает?», «Где мы теряем маржу?», «Какой регион не выполняет KPI?». Для ответа требовался запрос в IT, ручной сбор данных, подготовка презентации.
Цели проекта: от «иметь отчеты» к «управлять в реальном времени»
Мы сформулировали 4 стратегических приоритета:
Оптимизация процессов — сократить время на сбор показателей с 3-5 дней до нескольких часов, устранить ручные операции
Прозрачность данных — обеспечить доступность и понятность данных для всех подразделений
Качество аналитики — повысить достоверность и глубину анализа для стратегических решений
Единая модель — создать корпоративную модель данных с визуализацией и мониторингом в реальном времени
Выбор платформы: почему Visiology
Мы рассматривали несколько вариантов: Power BI, Qlik, Tableau, собственная разработка. Visiology выбрали по 4 критериям:
Экспертиза и репутация
Лидер российского рынка enterprise BI с кейсами у «Газпромбанка», «Магнита», «Леруа Мерлен» и других крупных игроков. Это не поставщик, а партнер, который понимает специфику российского бизнеса и готов к глубокой интеграции.
Гибкая архитектура
Поддержка гибридных развертываний (облако + локальная инфраструктура) — критично для compliance и требований InfoSec. Возможность подключения разнородных источников: от 1С до IoT-датчиков на технике.
Интерфейс и юзабилити
Для конечных пользователей (менеджеров, руководителей регионов) интерфейс оказался проще и интуитивнее альтернатив. Это снизило барьер внедрения и затраты на обучение.
Сообщество и поддержка
Большое комьюнити, доступное обучение, быстрая экспертная поддержка. Важно: легче найти специалистов, чем на экзотических платформах.
Архитектура решения: корпоративная шина данных
Мы не просто «подключили дашборды». Построили корпоративную шину данных на базе Visiology:
text
Источники данных → ETL/ELT → Единое хранилище → Витрины данных → Дашборды/Аналитика ↓ ↓ Контроль качества Мобильное приложение ↓ ↓ Метаданные и линейность Алармы и оповещения
Технические компоненты:
10+ источников: 1С (бухгалтерия, управленческий учет), Bitrix (CRM), телематика (GPS/датчики техники), системы учета рабочего времени, Excel-файлы
Корпоративная модель данных: единая терминология, мастер-данные (техника, клиенты, сотрудники), линейность данных (от источника до дашборда)
Витрины данных: специализированные наборы для разных бизнес-направлений (операционная эффективность, финансы, продажи, техническое обслуживание)
Визуализация: еженедельные дашборды для оперативного управления, стратегические дашборды для C-level, мобильные дашборды для руководителей в полях
Мониторинг и алармы: мгновенные уведомления о критических отклонениях (простой техники, провала KPI, рисков безопасности)
Цифры и результаты: что изменилось за 12 месяцев
МетрикаБылоСталоИзменениеВремя подготовки отчетности3-5 дней2-3 часа-80%Достоверность данных80-85%95%+15%Количество источников данных10+ изолированных10+ интегрированныхЕдиная модельЧастота обновления данныхЕженедельноЕжедневно/в реальном времени+700%Время внедрения нового региона3-4 месяца2-3 недели-85%Процент ручных операций60%<10%-85%
Качественные изменения:
Руководители регионов получили доступ к своим дашбордам в реальном времени через мобильное приложение. Меньше вопросов к центральному офису — больше фокуса на клиентах.
Операционная эффективность: выявили 15% техники с низкой загрузкой, перераспределили между регионами, повысили доходность на 8%.
Стратегическое планирование: теперь видим не только историю, но и прогнозы на основе ML-моделей (Visiology встроенные алгоритмы).
Ключевые уроки для CIO
1. Начинайте с проблемы бизнеса, не с технологии
Мы не выбирали «BI-систему». Мы решали задачу: «Как управлять 2000 единицами техники в 22 регионах эффективно». Технология — это инструмент, а не цель.
2. Стройте корпоративную шину данных, а не просто дашборды
Дашборды без единой модели данных — это красивые картинки. Инвестируйте в построение единой терминологии, мастер-данных и линейности данных с первого дня.
3. Автоматизация > Визуализация
Визуализация важна, но главное — устранить ручные операции. 80% времени экономим не за счет «красивых графиков», а за счет автоматической интеграции и валидации данных.
4. Юзабилити для бизнеса — критичный фактор успеха
Если система требует 40 часов обучения — это провал. Выбирайте платформы, которые интуитивны для конечных пользователей. Иначе внедрение не взлетит.
5. Гибридная архитектура — не компромисс, а необходимость
Облако — быстрее, локально — безопаснее. Современные платформы должны поддерживать оба сценария. InfoSec и compliance не должны блокировать digital.
6. Масштабируемость — это не про «много серверов», а про «быстрое подключение новых бизнес-единиц»
Наша метрика: 2-3 недели на полное подключение нового региона. Если у вас это занимает месяцы — архитектура не готова к росту.
Что дальше: план на 2025-2026
Мы уже работаем над следующим этапом:
IoT-интеграция: подключение телематики напрямую к Visiology для предиктивного обслуживания техники
AI-ассистент для руководителей: нативная интеграция с мессенджерами для быстрых ответов «Почему падает выручка в регионе X?»
Расширение на экосистему: подключаем партнеров и поставщиков к нашей шине данных для end-to-end видимости цепочки
Заключение: почему это важно для CIO
В эпоху ИИ мир никого не ждет. Компании, которые продолжают решать «на глаз», уходят на обочину. А CIO, которые не могут предоставить бизнесу real-time аналитику, рискуют стать владельцами инфраструктуры, а не драйверами стратегии.visiology
ArLift — это не уникальный кейс. Это типовая ситуация для любой распределенной компании: розница, логистика, производство, сервис. Разница только в том, кто первым построит корпоративную шину данных и получит конкурентное преимущество.
Ваши действия сегодня:
Посмотрите, сколько временя уходит на сбор отчетности в вашей компании
Посчитайте, сколько ошибок в данных из-за ручного ввода
Оцените, сколько дней уходит на подключение нового бизнес-подразделения к аналитике
Если сумма больше 5 дней и 10% ошибок — вам нужно срочно менять подход.
Вопросы CIO в комментариях — отвечу, чем смогу. А на ViRush 2026 будем говорить про IoT и AI-ассистентов для управления техникой.
#CIO #BusinessIntelligence #DataDriven #Visiology #DigitalTransformation #EnterpriseBI
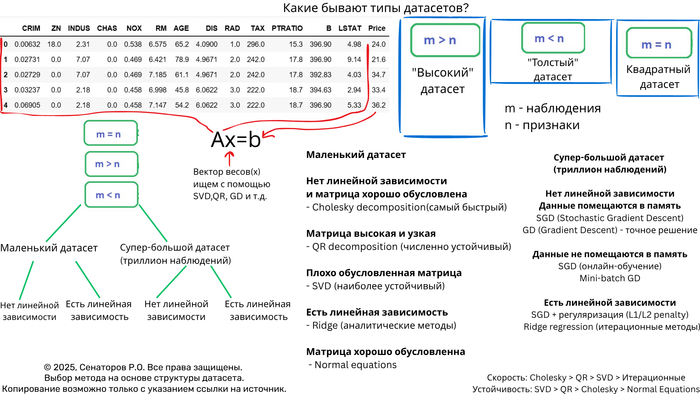
Выбор оптимального метода решения СЛАУ на основе анализа датасета
Полное руководство по выбору алгоритма для систем линейных уравнений
Меня зовут Руслан Сенаторов, я занимаюсь математическим обоснованием машинного обучения.
В этой статье, я расскажу как выбрать метод для определённого типа датасета, чтобы ваш код работал быстро, точно и без ошибок? И вы получили премию от руководства!
Введение
Решение систем линейных уравнений (СЛАУ) вида Ax = b — фундаментальная задача вычислительной математики и машинного обучения. Однако универсального метода не существует — выбор алгоритма критически зависит от характеристик датасета. Неправильный выбор может привести к катастрофическому замедлению вычислений или полной потере точности.
Ключевые характеристики датасета
1. Размер и структура матрицы
n_samples × n_features — соотношение наблюдений и признаков
Плотность/разреженность — процент ненулевых элементов
Обусловленность — число обусловленности матрицы
2. Вычислительные ограничения
Объем оперативной памяти
Требования к точности
Время вычислений
Дерево решений для выбора метода
Маленькие датасеты (n < 1000)
Плотные хорошо обусловленные матрицы
# Холецкий — самый быстрый для POSDEF матриц
if np.all(np.linalg.eigvals(A) > 0):
L = np.linalg.cholesky(A)
x = solve_triangular(L.T, solve_triangular(L, b, lower=True))
Матрицы общего вида
# QR-разложение — золотой стандарт
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
Плохо обусловленные системы
# SVD — максимальная устойчивость
U, s, Vt = np.linalg.svd(A, full_matrices=False)
x = Vt.T @ np.diag(1/s) @ U.T @ b
***
Средние датасеты (1000 < n < 10,000)
"Высокие" матрицы (n_samples >> n_features)
# QR остается оптимальным
# Сложность O(mn²) эффективна при m >> n
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
"Широкие" матрицы (n_samples << n_features)
# Итерационные методы или регуляризация
from sklearn.linear_model import Ridge
model = Ridge(alpha=1e-6, solver='lsqr')
model.fit(A, b)
x = model.coef_
***
Большие датасеты (n > 10,000)
Разреженные матрицы
# Итерационные методы
from scipy.sparse.linalg import lsqr
x = lsqr(A, b, iter_lim=1000)[0]
***
Огромные датасеты (n > 1,000,000)
Стохастические методы
from sklearn.linear_model import SGDRegressor
model = SGDRegressor(max_iter=1000, tol=1e-3)
model.fit(A_batches, b_batches) # Мини-батчи
Когда использовать нормальные уравнения?
"Высокие" матрицы (m >> n)
# Решение через нормальные уравнения
x = np.linalg.inv(A.T @ A) @ A.T @ b
# Или более устойчивый вариант
x = np.linalg.solve(A.T @ A, A.T @ b)
10000 наблюдений и 50 фитч - Идеально для нормальных уравнений
cond_number = np.linalg.cond(A.T @ A) # < 10^8 Хорошо обусловленная
Детальный анализ методов
Точные методы (прямые)
Итерационные методы
SGD | Подходит для огромных данных | Медленная сходимость
Заключение
Выбор оптимального метода решения СЛАУ — это искусство баланса между точностью, скоростью и требованиями к памяти. Ключевые рекомендации:
Маленькие матрицы → Прямые методы (QR/SVD)
Большие разреженные → Специализированные разреженные решатели
Огромные плотные → Итерационные методы с предобуславливанием
Экстремальные размеры → Стохастическая оптимизация
Главное правило: Всегда начинайте с анализа структуры и свойств вашей матрицы — это сэкономит часы вычислений и предотвратит численные катастрофы.
Используйте это руководство как отправную точку для выбора оптимального стратегии решения ваших задач линейной алгебры.
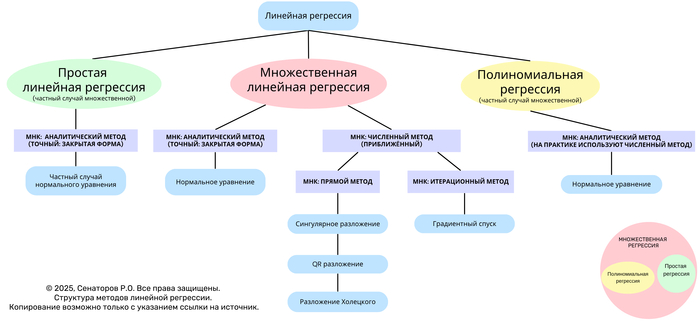
Roadmap linear regression (Структура методов линейной регрессии)1
Линейная регрессия — один из базовых методов статистического анализа и машинного обучения, предназначенный для моделирования зависимости отклика (зависимой переменной) от одной или нескольких независимых переменных.
Данное дерево отражает иерархическую структуру основных видов линейной регрессии и методов решения задачи наименьших квадратов (МНК) — от аналитических к численным и итерационным.
Общая структура
На верхнем уровне различают три формы линейной регрессии:
Простая линейная регрессия — частный случай множественной, когда используется одна независимая переменная.
Множественная линейная регрессия — базовая форма, включающая несколько независимых переменных.
Полиномиальная регрессия — частный случай множественной, в которой вектор признаков дополнен степенными преобразованиями исходных переменных.
Методы наименьших квадратов (МНК)
Решение задачи линейной регрессии сводится к минимизации функции ошибок (суммы квадратов отклонений между наблюдаемыми и предсказанными значениями).
В зависимости от подхода различают аналитические, численные и итерационные методы.
1. Аналитический метод (закрытая форма)
Применяется, когда матрица признаков имеет полную ранговую структуру и система допускает точное решение.
Решение выражается формулой:
normal equation
Используется в простой и множественной линейной регрессии.
Базируется на нормальном уравнении.
2. Численные методы (приближённые)
Используются при больших объёмах данных или плохо обусловленных матрицах.
Основаны на разложениях матриц:
Сингулярное разложение (SVD)
QR-разложение
Разложение Холецкого
Обеспечивают численную устойчивость и более эффективные вычисления.
3. Итерационные методы
Применяются при очень больших данных, когда аналитическое решение невозможно вычислить напрямую.
Основной подход — градиентный спуск, при котором веса обновляются пошагово:
Особенности полиномиальной регрессии
Полиномиальная регрессия представляет собой множительную регрессию, где вектор признаков дополнен степенными функциями исходных переменных.
Хотя аналитическая форма возможна, на практике применяются численные методы, обеспечивающие стабильность и точность вычислений при высоких степенях полинома.
Взаимосвязь моделей
На схеме представлена визуальная взаимосвязь:
Простая регрессия — частный случай множественной.
Полиномиальная — частный случай множественной с расширенным базисом признаков.
Все три формы объединяются через метод наименьших квадратов.
Значимость статьи и вклад в Data Science
Представленный древовидный роадмап методов линейной регрессии является первой в истории попыткой системно и визуально объединить все формы линейной регрессии — простую, множественную и полиномиальную — через призму методов наименьших квадратов (МНК), включая аналитические, численные и итерационные подходы.
Традиционно в учебной и академической литературе методы линейной регрессии рассматриваются фрагментарно:
отдельно описываются простая и множественная регрессии,
разрозненно излагаются методы решения (нормальное уравнение, QR, SVD, градиентный спуск),
редко подчеркивается иерархическая связь между ними.
Разработанная структура впервые:
Объединяет все виды линейной регрессии в едином древовидном представлении, где показаны отношения "частный случай – обобщение".
Классифицирует методы МНК по принципу:
аналитические (точные, закрытая форма)
численные (разложения матриц)
итерационные (оптимизационные процедуры)
Визуализирует связь между теориями линейной алгебры и машинного обучения, показывая, как фундаментальные методы (SVD, QR, Холецкий, градиентный спуск) вписываются в единую систему.
Формирует когнитивную карту обучения — от интуитивных понятий к вычислительным и теоретическим аспектам, что делает её удобной как для студентов, так и для исследователей.
Научная и практическая новизна
Впервые создана иерархическая модель линейной регрессии, отражающая связи между всеми основными вариантами и методами решения.
Предложен универсальный визуальный формат (древовидный роадмап), который объединяет как статистическую, так и вычислительную перспективы анализа.
Показано, что полиномиальная и простая регрессии являются не отдельными методами, а вложенными случаями множественной регрессии.
Дана структурная типология МНК, которая ранее отсутствовала в учебных материалах и научных публикациях в таком виде.
Работа имеет прикладную значимость для Data Science, так как облегчает построение ментальной модели всех алгоритмов регрессии и их реализации в библиотечных инструментах (NumPy, SciPy, scikit-learn).
Вклад в Data Science
Для практиков Data Science роадмап служит навигационной схемой:
он показывает, какой метод выбрать в зависимости от типа задачи, объёма данных и требований к точности.Для преподавателей и студентов он обеспечивает структурную основу обучения, позволяя переходить от интуитивного понимания к строгим математическим методам.
Для исследователей — даёт целостное представление об эволюции МНК и связи между аналитическими и численными методами, что важно при разработке новых алгоритмов оптимизации и регуляризации.
До момента публикации не существовало единой визуальной структуры, описывающей всю иерархию методов линейной регрессии в рамках одной системы координат