Добрый день. Не очень силен в математике, но интересует такой вопрос:
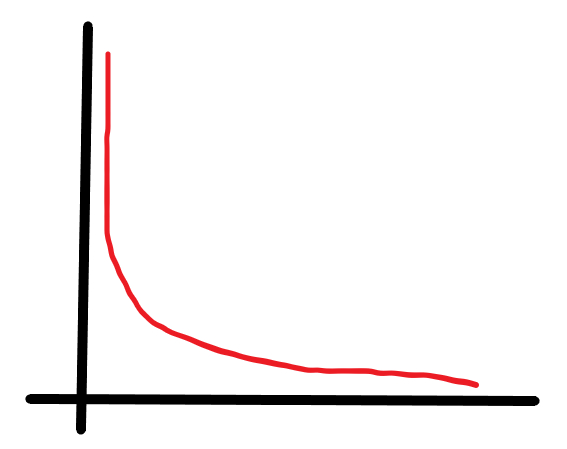
Как определить гиперболу, вписанную в определенный угол, например так:
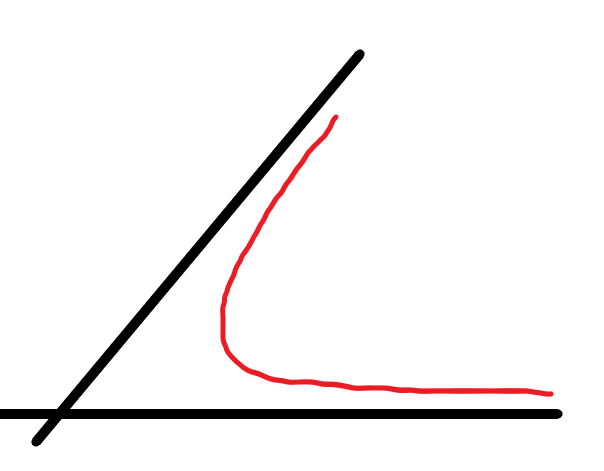
или вот так:
интересует для произвольного угла, и вообще существует ли решение?
от чего будет в данном случае зависеть формула кривой, если известен угол наклона (диапазон 0-90 градусов к примеру).
Вопрос сугубо практический, делаю игру, и не пойму, как строить алгоритм в данном случае.
такой алгоритмЭто какой? Зависимость радиуса от скорости для варианта с нормалью? Можно либо добавить константу, чтобы всегда был минимальный "радиус", либо сделать минимальную скорость змейки.
ну построю алгоритм, и дальше останется записать его на паскале
делов то
меня задерживает только алгоритм
такой алгоритмЭто какой? Зависимость радиуса от скорости для варианта с нормалью? Можно либо добавить константу, чтобы всегда был минимальный "радиус", либо сделать минимальную скорость змейки.
Можно и так, только радиус скругления тогда должен быть функцией от скорости (больше скорость - больше радиус), а в предложенном мной варианте это вытекает само собой =)
как мог реализовал такой алгоритм - он неплохо ведет себя при отклонении на небольшие углы, и позволяет рисовать достаточно плавные кривые
но есть проблема при резком изменении вектора направления - получается острый пик, не знаю, как это исправить пока:
Можно и так, только радиус скругления тогда должен быть функцией от скорости (больше скорость - больше радиус), а в предложенном мной варианте это вытекает само собой =)
А тебе точно нужно траекторию вычислять? Если нужен именно рисунок траектории в каких-то модельных ситуациях, то это, может, и хороший подход. Если же хочется сделать именно движение змейки в динамике, то предложенный JohnD03 вариант выглядит наиболее интуитивным и наименее мудреным. Все равно игра будет работать тактами, и от честной гладкой окружности толку не будет, ее все равно придется дискретизировать. И поэтому вычисление окружностей в итоге, скорее всего, окажется эквивалентным шагом, но более сложным. При этом все равно придется вводить проверку, произошло ли отклонение от прямой траектории достаточно сильное, чтобы уже выходить на окружность, или нет, а в предложенном варианте эта проверка уже встроена в сам метод.
щас обдумываю промежуточный вариант, где главной будет процедура поворота по радиусу в зависимости от колебаний вектора направления
Ну и так, у нас сегодня вышла прям идеальная иллюстрация - https://ru.wikipedia.org/wiki/Проблема_XY
http://mathprofi.ru/giperbola_i_parabola.html
Берём формулу гиперболы, берём формулу её асимптот, через кручу-верчу-запутать-хочу тригонометрические функции высчитываем соотношение b/a, потом константой "натягиваем" до нужного графика. На каком этапе проблема?
Ну и так, у нас сегодня вышла прям идеальная иллюстрация - https://ru.wikipedia.org/wiki/Проблема_XY
посидел и осенило:
в точке поворота делаем нормаль, высотой, равной радиусу скругления
и она уже будет считаться центром круга
и делаем поворот на нужный угол, так, чтобы все точки ложились на траекторию круга
все гениальное просто
Дискретизацию змейки увеличить, разрешенный угол/фрейм уменьшить.
Имхо, лучше сделать хоть какой-то прототип из говна и палок, и потом уже допиливать детали, если что-то не устраивает, чем долго и нудно убивать всё желание избыточно сложными формулами пока их даже не на чем проверить.
Имхо, мысль в первую минуту и явно может быть оптимизирована -
1) регистрируется вектор движения (скорость и направление) и все "точки" змейки.
2) направление вектора не может изменяться быстрее чем Х градусов/единица времени (фрейм, скорее всего).
Это же и обеспечивает закруглённость, т.е. если надо повернуть на 170 градусов, а можно не более чем на 10 за фрейм - то будет 17 фреймов на "поворот", где каждая точка будет смещена на длину сегмента и угол в 10 градусов в сторону точки назначения
3) "точки" змейки удаляются под хвостом и появляются перед мордой в процессе движения, при этом сами не двигаются (либо двигаются первые несколько, но это излишнее усложнение)
тоже думал за временной лаг перед поворотом, но не знаю, будет ли достаточно этого для гладкости
Так а как тебе тут гиперболы помогут? При наличии ломаной с более чем двумя звеньями уже не получится гладкой кривой.
Сглаживание ломаных уже давно придумано, вот примеры. Советую изучить уже наработанную теорию, чтобы не изобретать велосипед.
https://ru.wikipedia.org/wiki/Кривая_Безье
https://en.wikipedia.org/wiki/B-spline
ок, спасибо, попробую копнуть в этом направлении
если совсем закапаюсь, придется какой-нибудь движок учить
А траектория чего именно, вообще говоря, и почему с современными игровыми движками нужно прописывать такой "низкий" уровень, а не отдать на откуп, например, простой физике, с инерцией и всяким таким?
хочу сделать вот такое:
https://vseigru.net/igry-zmejka/25998-igra-gulper-io.html
но не на готовом движке, а чисто программно, например на дельфи
Ну и да, если нужен угол между асимптотами - проще всего "располовинить" угол из расчётов выше, поделив на два.
т.е. tan(60deg/2) = tan(30deg), ну и дальше по тексту.
Тогда рисуется такое:
https://www.wolframalpha.com/input/?i=(x^2+/+sqrt(3)^2)+-+(y^2+/+1^2)+=+1
я тут подумал, что может быть сильно все усложняю, и задачу можно решить проще?
суть предполагаемого алгоритма заключается в том, чтобы обеспечить сглаживание траектории при изменении направления, например, чтобы было
вместо аналогичной траектории но с ломанными отрезками?
Наклона относительно чего? относительно оси абсцисс?
Школьная геометрия же.
y = tan(60deg)*x
y = sqrt(3)*x - формула одной из асимптот
при этом же, из формулы асимптот:
y = (b/a)*x
(b/a)*x = tan(60deg)*x
(b/a) = tan(60deg)
b/a = sqrt(3)
Дальше умножьте на нужную вам константу чтобы смасштабировать куда вам надо, подставьте в каноническое уравнение и рисуйте.
Какие проблемы?
Пример при a=1:
https://www.wolframalpha.com/input/?i=(x^2+/+1^2)+-+(y^2+/+sqrt(3)^2)+=+1
Наклона относительно чего? относительно оси абсцисс?
Школьная геометрия же.
y = tan(60deg)*x
y = sqrt(3)*x - формула одной из асимптот
при этом же, из формулы асимптот:
y = (b/a)*x
(b/a)*x = tan(60deg)*x
(b/a) = tan(60deg)
b/a = sqrt(3)
Дальше умножьте на нужную вам константу чтобы смасштабировать куда вам надо, подставьте в каноническое уравнение и рисуйте.
Какие проблемы?
Пример при a=1:
https://www.wolframalpha.com/input/?i=(x^2+/+1^2)+-+(y^2+/+sqrt(3)^2)+=+1
Лига математиков
958 постов2.5K подписчик