Трение
Показать полностью
0 просмотренных постов скрыто
Основные силы в настройке пианино: трение, обмотка струны вокруг колка и вызовы точной работы
Настройка пианино — это не только искусство, но и сложный инженерный процесс, в котором участвуют десятки механических факторов. В старых моделях, таких как Steinway Model 45 (1977 года), этот процесс особенно осложняется высокими силами трения, сопротивлением пружинящих обмоток и взаимодействием струн с пинблоком. Советы профессионалов, таких как Бекет, помогают разобраться с этой сложной задачей и предлагают решения, основанные на многолетнем опыте. https://forum.pianoworld.com//ubbthreads.php/topics/3594341.html#Post3594341
1. Почему трение создаёт проблему?
Конструкция пианино с высоким V-баром создаёт резкий угол перелома струны, что значительно увеличивает трение в точке контакта. Это трение усугубляется за счёт:
Эластичной деформации струны, когда она изгибается вокруг V-бара.
Сопротивления обмоток струны на пинблоке, особенно если витки обмотки плохо выровнены или недостаточно плотно прижаты.
Хотя под струнами установлен фетр, чтобы немного облегчить скольжение, он не в состоянии полностью компенсировать высокое трение и сильное натяжение струны. Это создаёт ситуации, когда настройка требует чрезмерных усилий, а точные микрошаги становятся почти невозможными.
2. Законы Ньютона в настройке пианино
Первый закон Ньютона (инерция): Статическое трение в точках контакта струны с V-баром и пином сопротивляется её движению. Для преодоления этого трения требуется приложить значительное усилие, что приводит к резким и неконтролируемым изменениям при настройке.
Второй закон Ньютона (сила и ускорение): Усилие настройщика должно не только преодолевать сопротивление трения, но и работать против дополнительного сопротивления плохо сжатых обмоток. Это приводит к нестабильной настройке, где струна "скачет" между состояниями статического и динамического трения.
Третий закон Ньютона (действие и противодействие): Каждое усилие настройщика — будь то вращение пина или работа с обмотками — вызывает реактивную силу со стороны струны и пинблока. Эти силы усиливают "пружинящий эффект," усложняя тонкую настройку.
3. Струна как защемлённая балка
С точки зрения механики, струна пианино ведёт себя как защемлённая балка с закреплением в двух точках — мостике и пинблоке. Эта система включает:
Упругую деформацию: Струна изгибается под натяжением, что создаёт локальные концентрации напряжений на V-баре и пинблоке.
Вибрационные силы: Струна вибрирует как два сегмента — между мостиком и V-баром, а также между V-баром и пинблоком. Любое неправильное натяжение или смещение нарушает эти вибрации, что влияет на стабильность настройки и качество звука.
Перераспределение натяжения: Каждое движение пина перераспределяет нагрузку, создавая дополнительное сопротивление в местах контакта.
4. Что советует Бекет? Правильная настройка обмоток
Бекет подчёркивает, что состояние обмоток струны на пинблоке является ключевым фактором успешной настройки. Он предлагает:
Уменьшить натяжение струны с обеих сторон, чтобы ослабить напряжение в точке перелома.
Выравнивание обмоток: Потянуть струну вверх с обратной стороны пина и постучать по обмоткам с передней стороны, чтобы добиться плотного прилегания витков.
Обеспечение плотности: Тесно прижатые обмотки снижают скольжение и обеспечивают равномерное сопротивление при настройке.
Правильное выравнивание обмоток уменьшает общее трение и делает струну более отзывчивой, что позволяет добиться высокой точности настройки.
5. Механические расчёты: почему настройка требует усилий?
Силы, действующие при настройке пианино, включают:
Крутящий момент натяжения струны: Постоянное усилие, с которым струна тянет пин назад.
Крутящий момент трения: Сопротивление между пином и пинблоком.
Крутящий момент обмоток: Пружинящее сопротивление витков струны.
Общая сумма этих моментов составляет около:
M total = M tension + M friction + M spring
Based on empirical data, the total resistive torque is approximately:
M total ≈ 4.82 N·m
However, the actual torque required to achieve effective and precise adjustments of the tuning pin typically exceeds this value:
M required = 13 N·m
This implies that the tuner must provide an additional torque to compensate for the difference:
M shortfall = M required – M total ≈ 8.18 N·m
6. Вывод: почему фетр не спасёт?
Хотя фетр помогает немного снизить трение, основная проблема заключается в конструкции струны и её взаимодействии с пином и V-баром. Высокое трение, упругость струны и плохо настроенные обмотки создают систему, где значительная часть усилий тратится на компенсацию механических потерь.
Советы Бекета по правильной компрессии обмоток струны дают практическое решение этой проблемы. Правильно выровненные витки уменьшают трение, повышают отзывчивость струны и делают настройку более стабильной. Это показывает, что даже небольшие исправления механики могут существенно повлиять на результат.
Настройка пианино — это искусство, требующее точности и понимания сложной механики инструмента. Работая с такими нюансами, как обмотки и трение, вы добиваетесь идеального звучания — каждая нота становится результатом упорного труда и знаний. 😊
Показать полностью
Спор с коллегами
Сегодня после обеда идя на курилку я прокатился пару раз по льду в своей обуви, а коллега постарше - сказал этого не делать тк если кататься в обуви по льду(ну все возможно немножко разбегались и проезжали по скользкому месту) то она становится более скользкой, и у нас как бы состоялся спор- я ему сказал, что если и есть какое то влияние льда на подошвы моей обуви при скольжении, то им вполне себе можно пренебречь, и более скользкими от такого действия они не станут, а чтобы это как то повлияло на подошву- так мне нужно годами кататься по льду. И вот мы никак это разрешить не смогли. Может кто-то может посчитать))? Или сказать мне , что я не прав)? Или наоборот прав, с какими то док-вами. Я ссылался на то, что коэффициент трения у льда крайне мал. И как бы вот)?
Хороший урок моей жизни
Я после слов учителя физики о том, что силой трения можно пренебречь
Воздух охлаждает/нагревает
Вентилятор разгоняет воздух, по сути просто ускоряя конвекцию тела. Метеор же сгорает в плотных слоях атмосферы из-за трения. Вопрос: с какой скоростью нужно двигаться в атмосфере, чтобы воздух начал нагревать, а не остужать? Где эта точка перехода?
Сгибание пачки пластиковых листов помогло разобраться с трением
Физики теоретически и экспериментально изучили процесс сгибания пачки пластиковых листов, чтобы понять какую роль в этом процессе играет трение между слоями. Для этого они разработали модель пачки, в которой трение выступает в роли малого возмущения. Построенная модель полностью описала реальное поведение листов и помогла понять, как происходит рассеяние энергии в такой системе. Исследование опубликовано в Physical Review Letters.
Человечество имеет дело со слоистыми структурами в различных отраслях науки и техники и на разных масштабах, начиная от многослойного графена и заканчивая слоями горных пород. Во всех случаях взаимодействие между слоями влияет на свойства структуры как целого. С точки зрения прикладной механики слоистые структуры обладают свойством рассеивать энергию, что используется, например, в рессорах.
Такая практическая польза служит мотивацией к теоретическому и экспериментальному исследованию деформаций в многослойных объектах. К настоящему моменту физики уже научились моделировать процессы в системах с небольшим числом слоев, либо там, где эффекты трения преобладают над всеми остальными эффектами, однако полноценной модели, связывающей микроскопические свойства системы с ее макроскопическим механическим откликом для деформаций произвольной амплитуды, так построено и не было.
В новой работе группа физиков из Швейцарии и Франции под руководством Педро Рейса (Pedro Reis) из Федеральной политехнической школы Лозанны продвинулась на шаг в этом направлении, исследовав процессы деформации толстой пачки эластичных листов. Листы были изготовлены из полиэтилентерефталата с длинной 220 миллиметров, шириной 30 миллиметров и толщиной 0,286 миллиметров. Число листов в пачке варьировалось от 1 до 70, а сами они были отшлифованы с обеих сторон наждачной бумагой, чтобы избежать адгезии и обеспечить сухое трение.
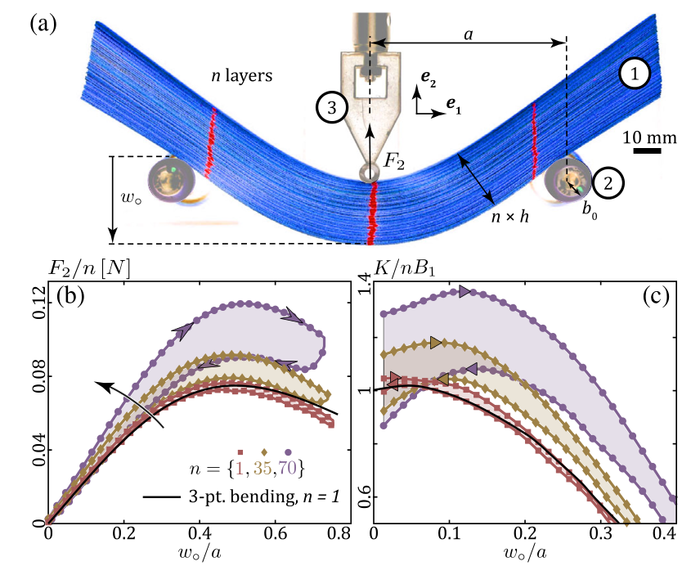
Пачка подвергалась испытанию на трехточечный изгиб. Нижние опоры представляли собой два валика, покрытых тонким слоем винил-полисилоксана для борьбы со скольжением и установленных на воздушные подшипники. Сверху на пачку давил идентор, который обеспечивал измерение силы реакции опоры от пачки. Для каждого эксперимента измерение проводилось путем подвода и отвода идентора, двигающегося с постоянной скоростью один миллиметр в секунду.
(a) Фотография экспериментальной установки. (b) Кривые подвода-отвода, показывающие зависимость силы, приходящейся на один лист, от глубины прогиба для 1 (квадраты), 35 (ромбы) и 70 (кружки) листов в пачке. Сплошной черной линией показана зависимость для простой однолистовой модели. (c) То же, что и (b), но для нормированной инкрементальной жесткости.
В результате серии экспериментов физики установили зависимость силы, приходящейся на один лист, от глубины прогиба пачки. Для одного листа эта зависимость хорошо описывается классической линейной моделью, разработанной ранее. Однако для большего числа листов авторы обнаружили, что результирующая сила, с которой пачка действует на индентор, больше, чем просто алгебраическая сумма сил от каждого листа по отдельности, что свидетельствует о нелинейном режиме отклика. Более того, строя кривые подвода-отвода они обнаружили гистерезис, что свидетельствует о диссипации энергии, то есть ее рассеянии в тепло в результате трения, причем диссипация была тем сильнее, чем больше было листов в пачке. Для описания нелинейного поведения системы физиками была введена и исследована инкрементальная жесткость пачки, которая в пределе малых отклонений равнялась сумме жесткостей отдельных листов.
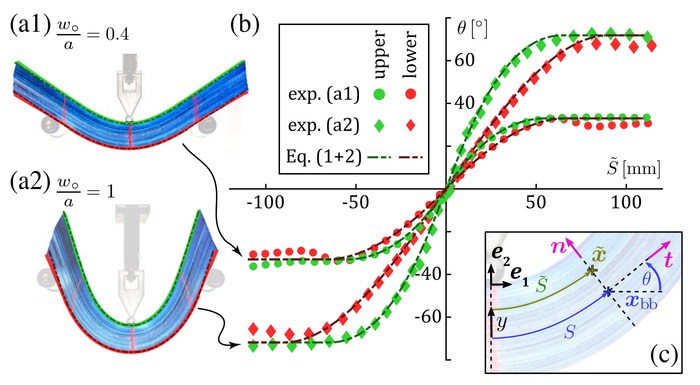
Помимо общего отклика физиков заинтересовало поведение отдельных листов. Для этого они нанесли сбоку пачки вертикальные отметки, чтобы следить, как эти точки будут смещаться в результате сгиба для каждого отдельного листа. Физики исследовали средний и сильный изгиб пачки из 70 листов и для каждого случая построили диаграммы, связывающие угол наклона листов с расстоянием между отметками на верхнем и нижнем листах. С ростом давления линии боковых отметок начали изгибаться, что свидетельствует о нарастании поперечного сдвига, точное описание которого, однако, в литературе отсутствовало.
(a) Фотографии пачки в режиме среднего (a1) и сильного (a2) изгиба. (b) Диаграммы, связывающие угол наклона листов с расстоянием между отметками на верхнем (зеленый) и нижнем (красный) листах в режиме среднего (кружки) и сильного (ромбы) изгиба. Пунктирными линиями показаны предсказания модели. (c) Рисунок с обозначениями, используемый авторами для вывода уравнений.
По этой причине физики построили новую модель, которая описывает толстые одномерные многослойные структуры с учетом трения. В ее рамках среди всех листов был выделен центральный лист с нулевым растяжением. Его авторы назвали «хребтом» пачки. Решив уравнение, описывающее этот слой, они смогли из геометрических соображений восстановить решения для всех остальных листов. Наконец, чтобы описать рассеяние энергии в системе и, соответственно, наблюдавшийся гистерезис, физики внесли в модель межслоевое трение как малое возмущение. Полученные решения продемонстрировали хорошее согласие с экспериментом.
Авторы подчеркивают, что развитая ими методология может быть применена к другим сложным системам, в которых трение играет важную роль. В частности, это может быть полезно при разработке устройств, предназначенных для рассеивания энергии, например, амортизаторов, гасителей, рессор и так далее. Физики отмечают также, что представленная модель сделана в квазистатическом приближении, при котором скорость изменения внешних сил много меньше, чем типичные времена процессов на микроуровне. Вместе с тем, они надеются построить в будущем такие модели, которые смогут учесть динамические и ударные условия.
Исследование механических процессов, происходящих при контакте разных материалов, представляет большой интерес для ученых. Ранее мы рассказывали, как физики обнаружили необычное поведение двух упругих тел, когда их сдавливают вместе, и предсказали эффект «сверхскользкости».
Показать полностью
2
О, сколько нам открытий чудных...
Показать полностью
3