Ответ на пост «Я гений или просто математику в школе не учил?»
Что-то навеяло и молодость вспомнил. Математику в школе особо не любил, да и вообще школу. Однако получал 4-5 особо не напрягаясь, и зачастую успевал решить контрольную и себе и соседу по парте. Т.е. склонность к этому была.
А любил я читать научную фантастику, и там регулярно встречались всякие многомерные пространства и их искривления. Правда, я как-то открыл учебник по топологии и там самые примитивные задачки показали, что вся эта фантастика сосет и причмокивает.
Но вот как-то обнаружил одно свойство пространств. И вот хотелось бы узнать как это в математике называется и когда это придумали.
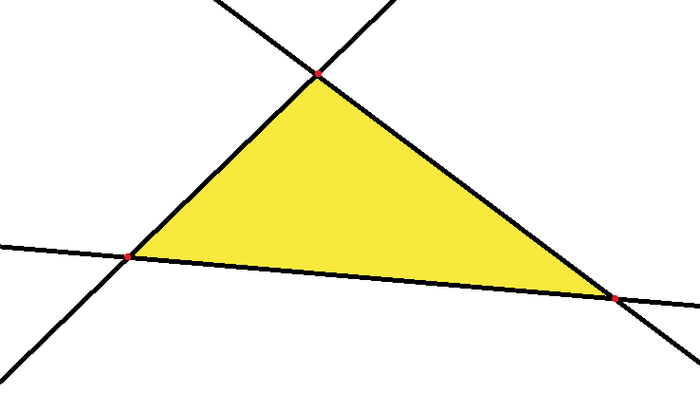
Начнем с простой задачи. Вот есть плоскость (двумерное пространство), и есть линии (одномерное пространства). Вопрос: сколько минимально нужно линий чтобы ограничить часть плоскости. Как нетрудно догадаться ответ: три.
А теперь поставим вопрос по другому: а сколько нужно пространств для ограничения N-мерного пространства.
Я думаю очевидно, что сколько точек не рисуй на плоскости, часть плоскости ты не ограничишь, а трехмерного пространства в двумерном вообще не может быть.
Т.е. для ограничения N-мерного пространства, нужны N-1 пространства.
Например для ограничения линии (одномерного пространства) нужны точки (т.е. точка это 0мерное пространство).
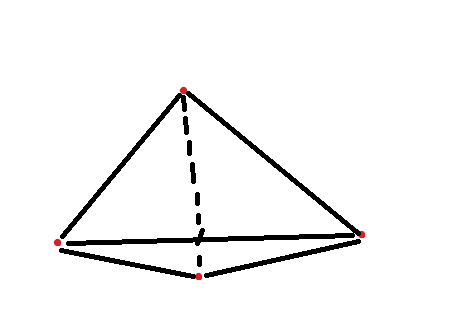
Для ограничения 3-хмерного пространства. Нужны четыре плоскости, т.е. пирамида.
И так первый и главный вывод.
Для ограничения 3-мерного пространства нужно 2-мерных пространств в количестве 4.
Для ограничения 2-мерного пространства нужно 1-мерных пространств в количестве 3.
Для ограничения 1-мерного пространства нужно 0-мерных пространств в количестве 2.
Для ограничения 0-мерного пространства нужно -1-мерных пространств в количестве 1.
Ну последний пункт это юмор такой. Однако тенденция на лицо.
Для ограничения N-мерного пространства нужно N-1-мерных пространств в количестве N+1.
Второй вывод:
Для ограничения 3-мерного пространства нужно 4 точки каждая из которых соединенна с другой точкой.
Для ограничения 2-мерного пространства нужно 3 точки каждая из которых соединенна с другой точкой.
Для ограничения 1-мерного пространства нужно 2 точки каждая из которых соединенна с другой точкой.
Для ограничения 0-мерного пространства нужна 1 точка (любопытный момент, обычно когда речь идет про пространства то они безграничны, а 0-мерное пространство получается ограниченным).На основании этого можно представить как выглядит часть четырехмерного пространства это 5 пирамид соединенные между собой всеми гранями.
Другой любопытный момент как выглядит проекция ограничения четрехмерного пространства на плоскости. Т.е. это 5 точек которые соединены между собой.
Свят-свят-свят
Еще раз повторю вопрос: как это называется в математике и когда это изобрели?