МатОлимп #11
Сегодня мы с вами попытаемся решить сложную задачку, которая предлагалась на Московской олимпиаде 1998 года.
Твой взгляд, когда кофе ещё не готов, а работать уже надо
Итак, все, кто хотел решить сам,наверняка уже решают, а мы продолжим.
Давайте посмотрим, какие остатки дают левая и правая часть при делении на 3 для этого составим табличку.
Тут можно сказать, что я пытаюсь схитрить. Ведь не факт, что любые степени будут давать такие же остатки. Ну хорошо. Разберёмся подробнее! Остатки от деления числа на 3 я буду обозначать как это же число с чертой сверху. Таким образом
А теперь заметим важное свойство! Остаток от произведения двух чисел есть остаток от произведения двух остатков.
Докажем этот факт и будем иметь все необходимое для доказательства задачи!
Если число a даёт остаток n при делении на 3, то его можно записать в виде a=3q+n. Аналогично, если b даёт остаток m, то b=3r+m. Перемножим a и b!
Итак, утверждение доказано. Тогда подтвердим нашу табличку!
Получается, что слева у нас всегда остаток 0+1=1, а справа либо 1 , либо 2. Но так как выражения равны, справа должен быть остаток 1. Следовательно, z - четное число.
Теперь разберёмся с остатками на 4!
Отсюда следует,что x тоже четное. Обозначим z=2n, x=2m. Наше уравнение можно переписать в следующем виде.
Таким образом, левая часть разлагается на множители. Но правая часть может делится только на числа вида 2^k. Значит, получаем следующее выражение
Но погодите! 3^m всегда нечетно, а правая часть четная, кроме случая, когда k=1. Значит, обязательно k=1. Отсюда получаем, что
Аналогично, правая часть - делители левой. Но у левой части у нас делители -степени тройки. Но в правой части два сомножителя различаются на 2. Это возможно только тогда, когда меньший из сомножителей - 1. Значить 2^(y-1)-1=1. Следовательно, y=2. Подставляя эти значения в решение системы уравнений, получаем, что n=1 и m=1. Значит z=x=2. Т.е. решениями являются Пифагоровы тройки и других решений нет! Задача решена и можно пить кофе!


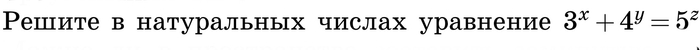


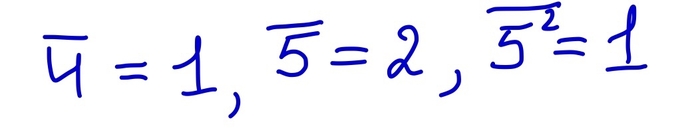
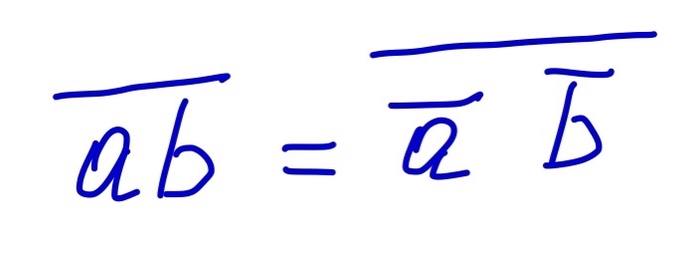
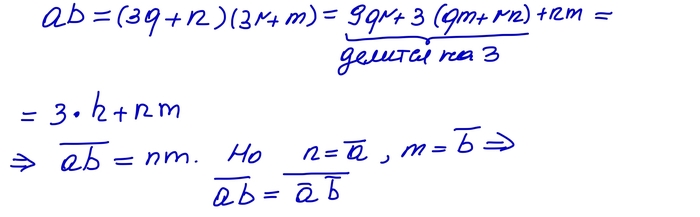
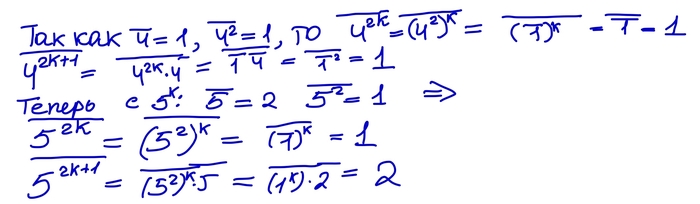
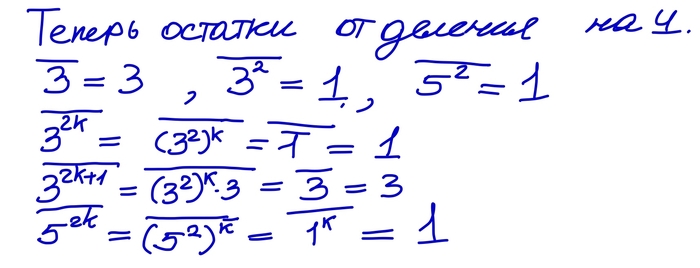
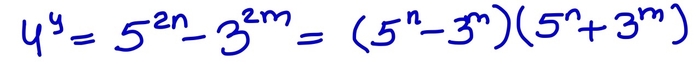
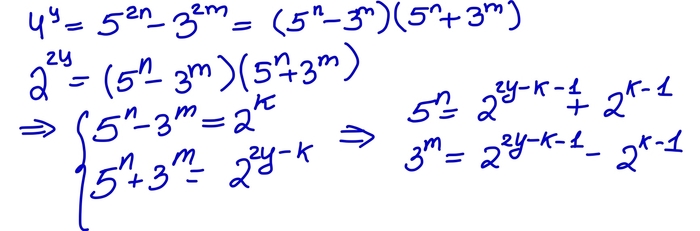
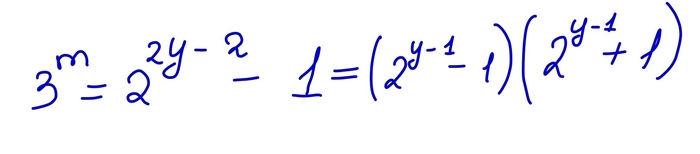
Лига математиков
914 постов2.5K подписчика