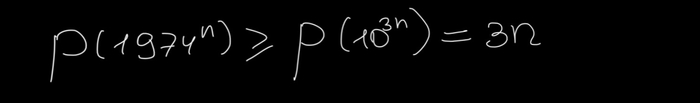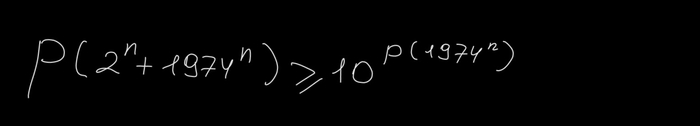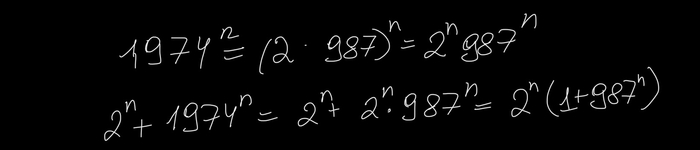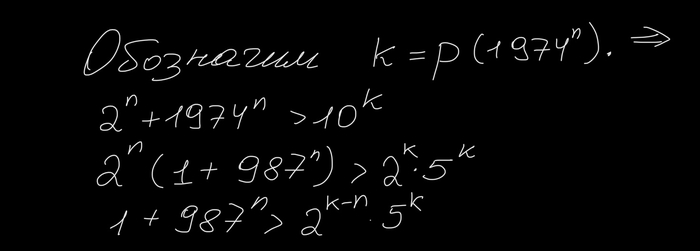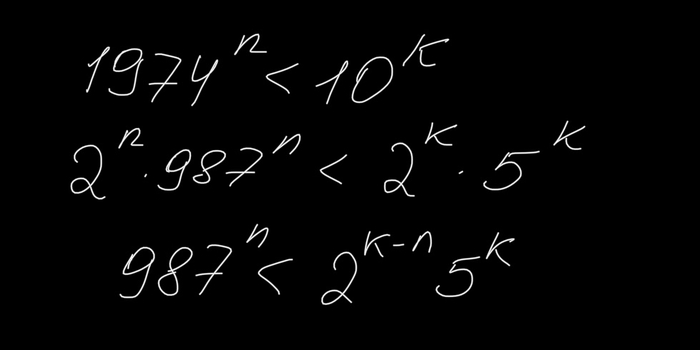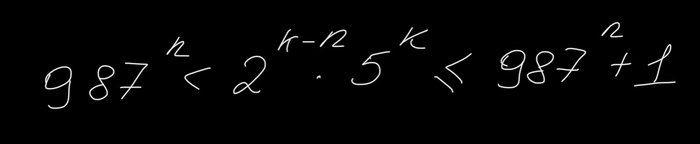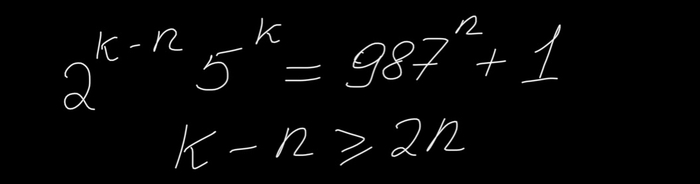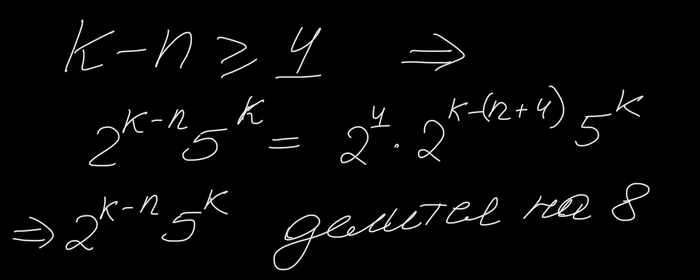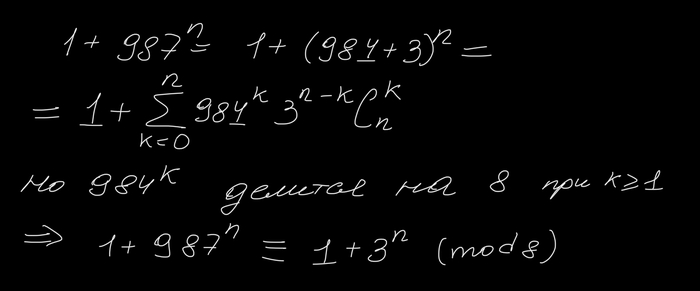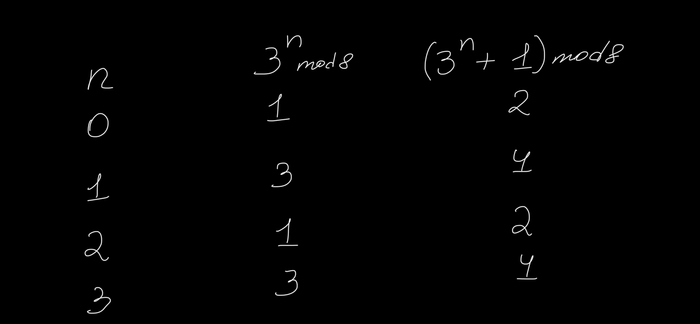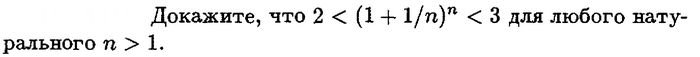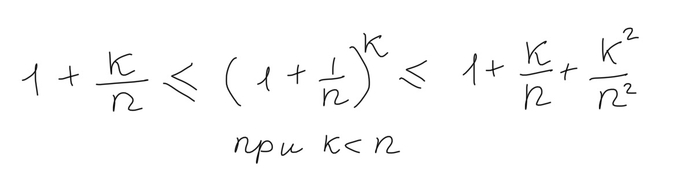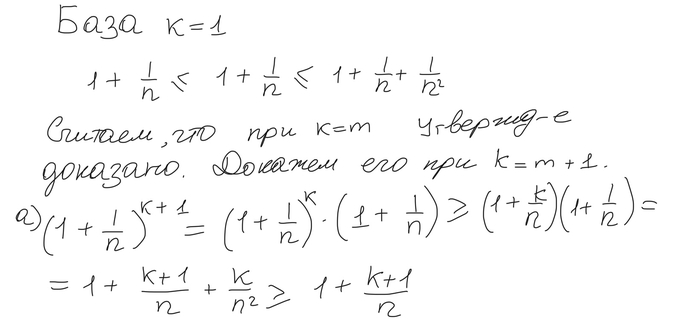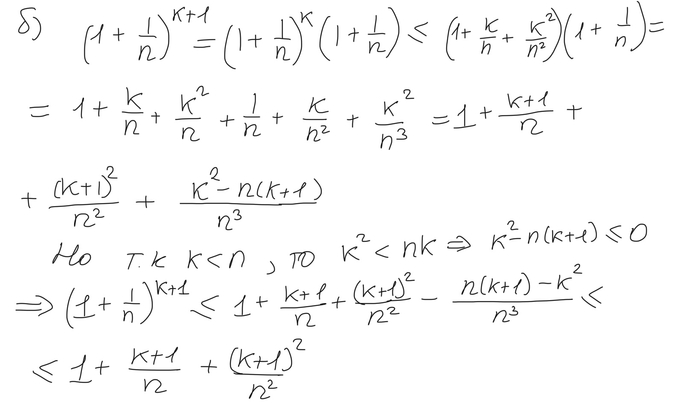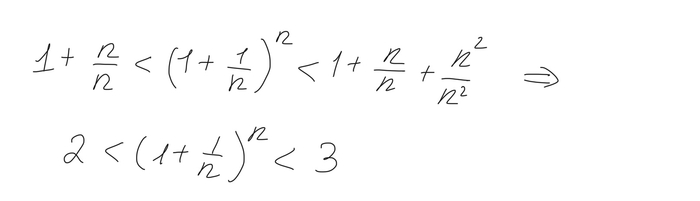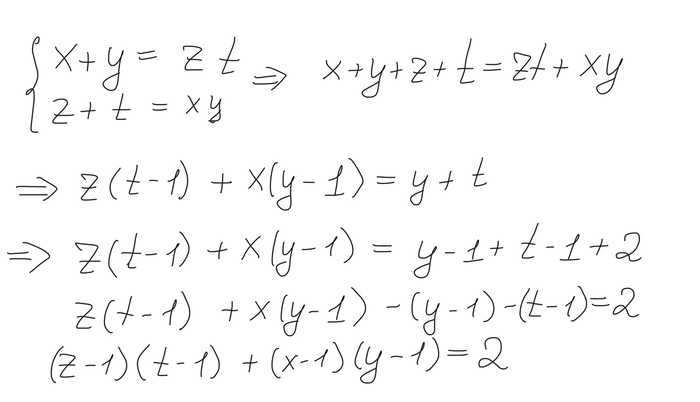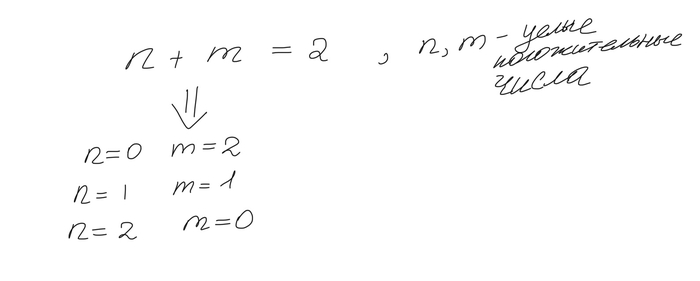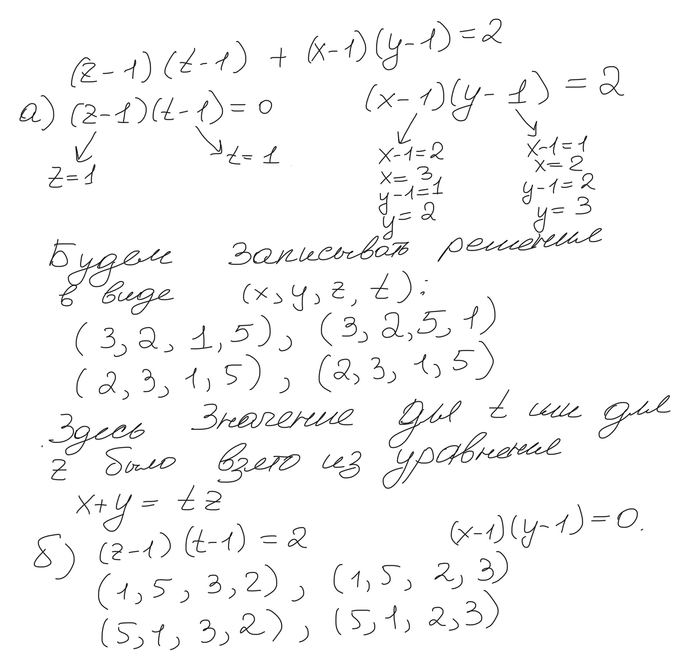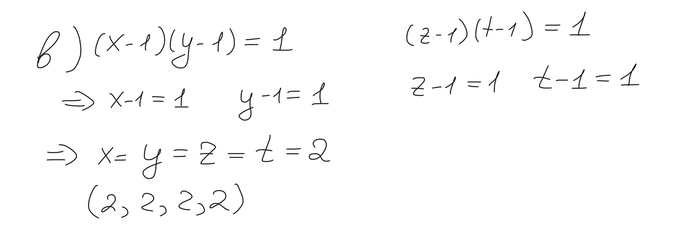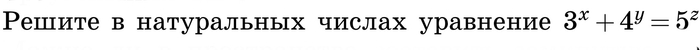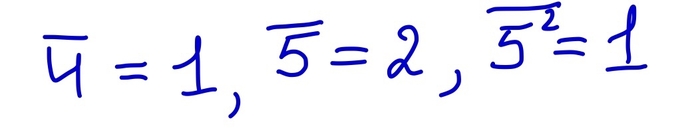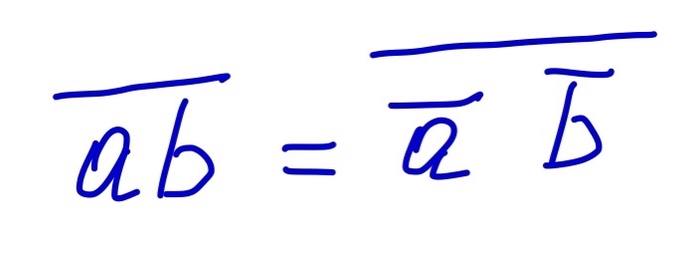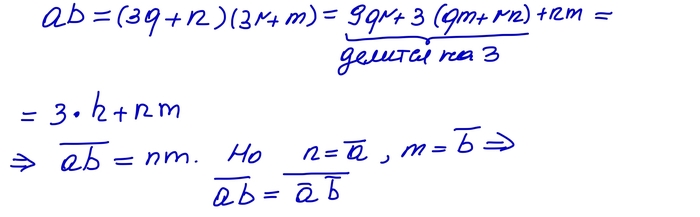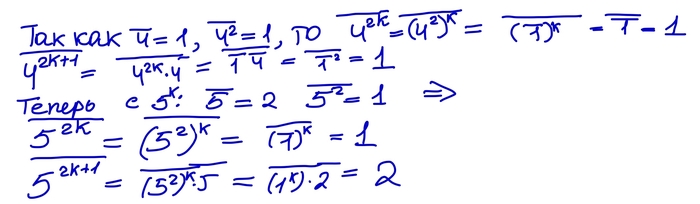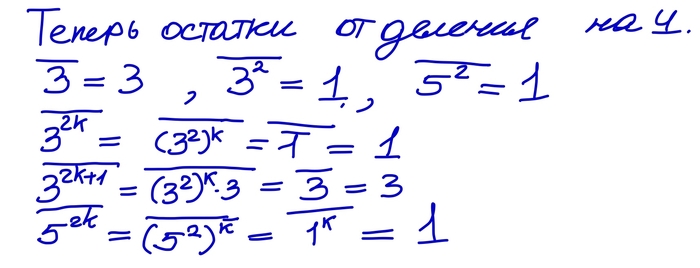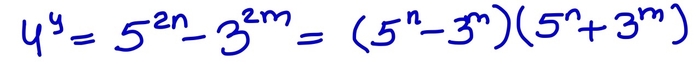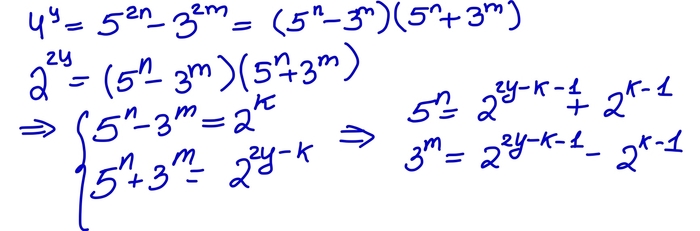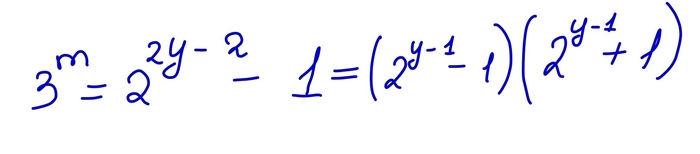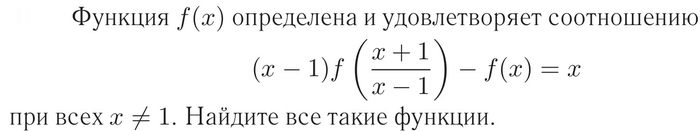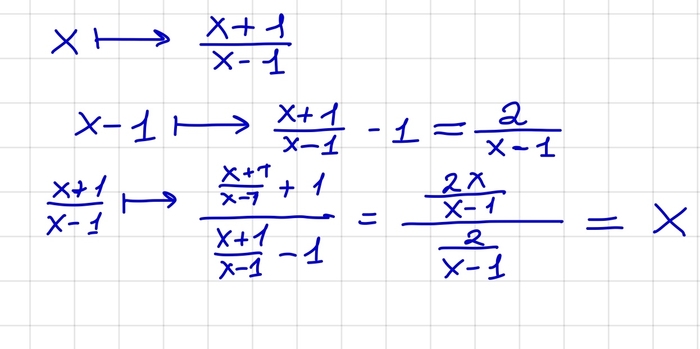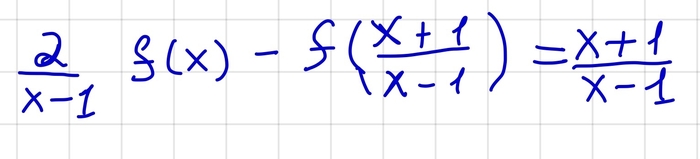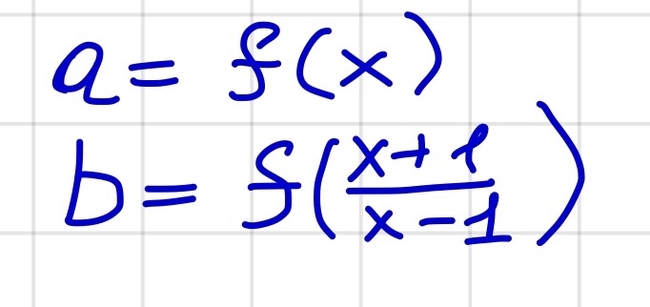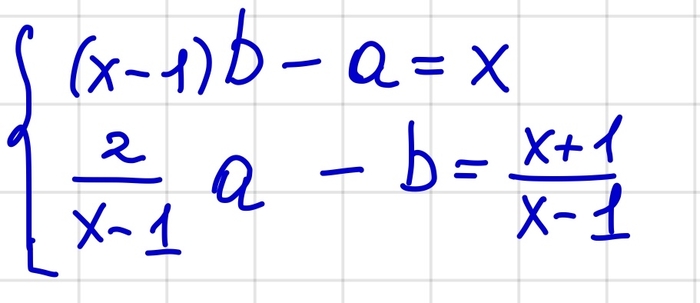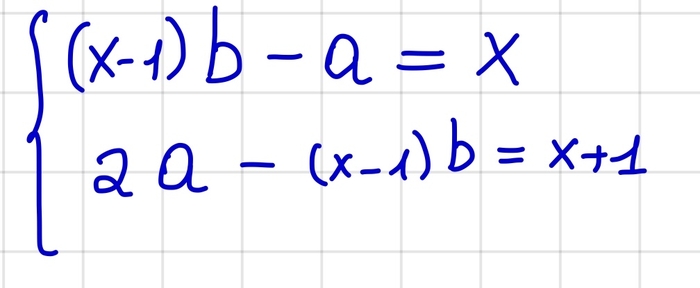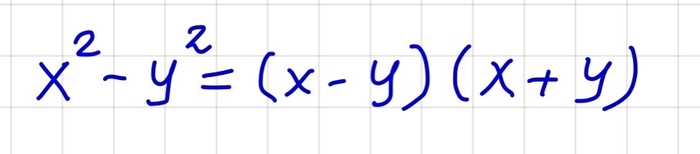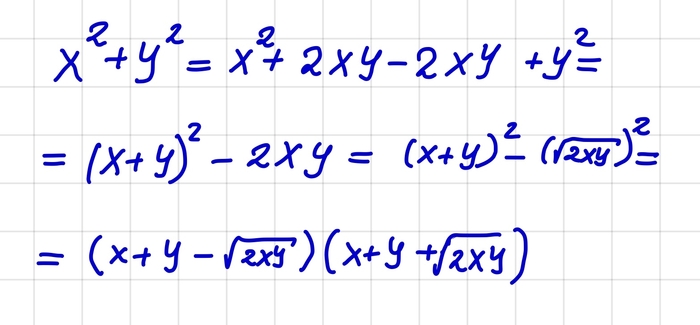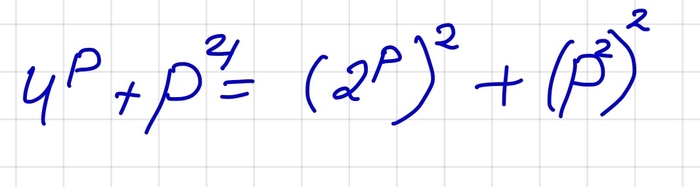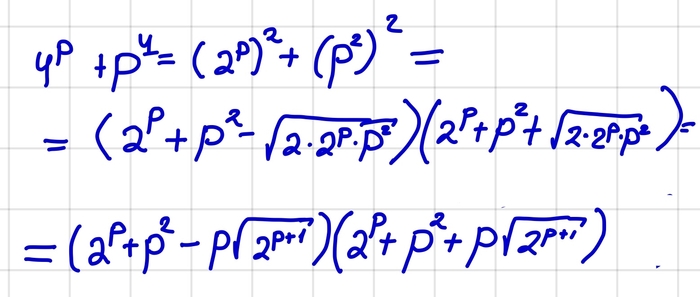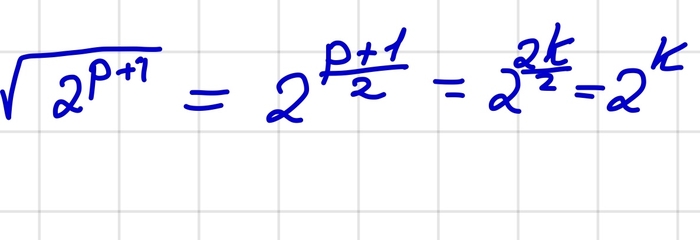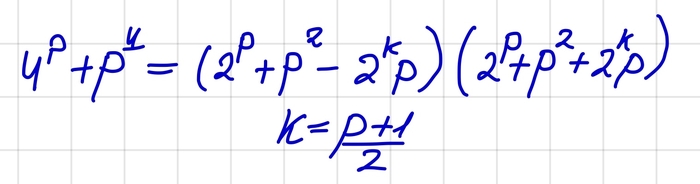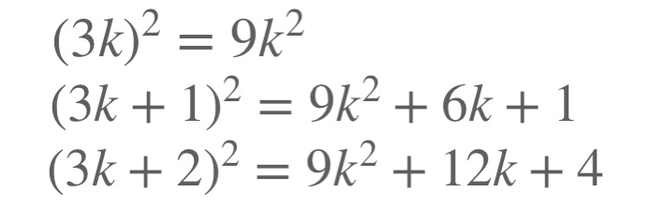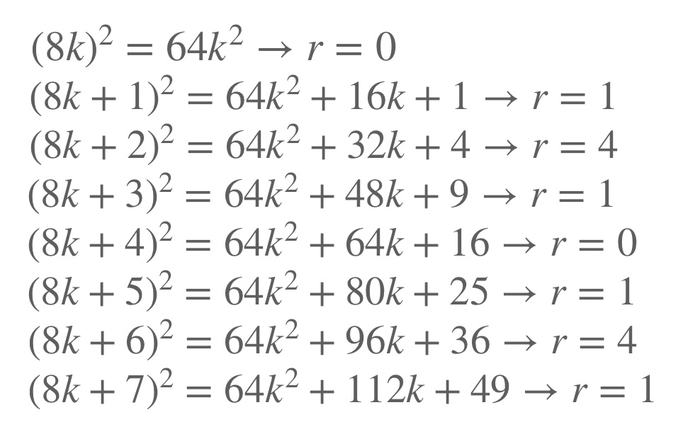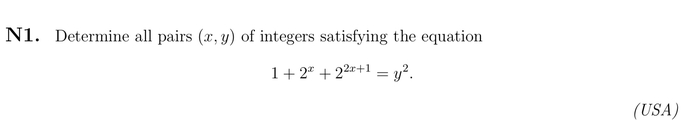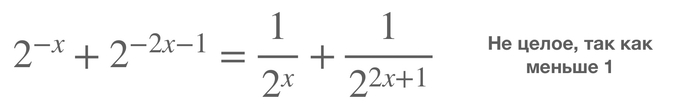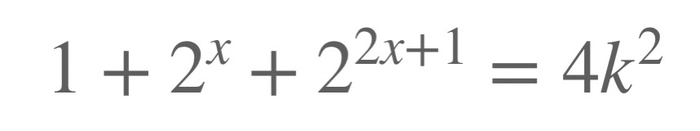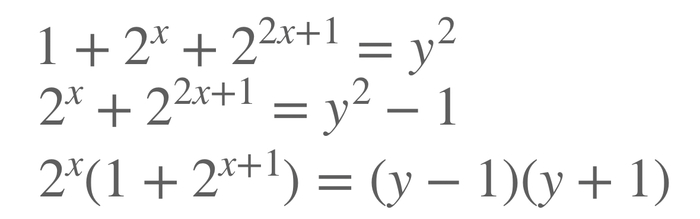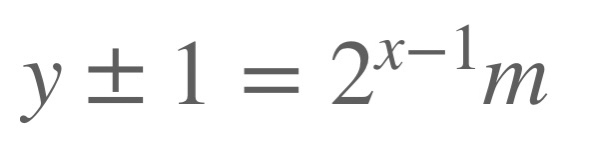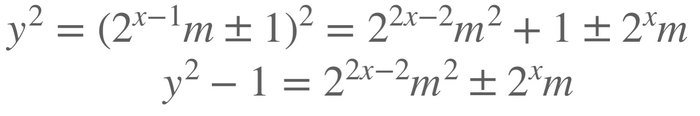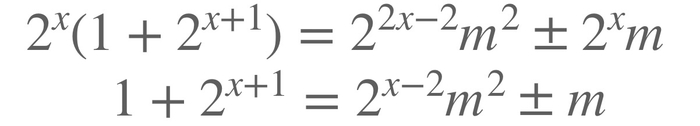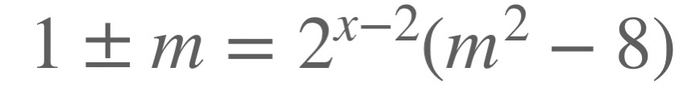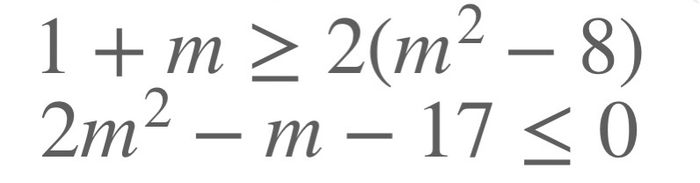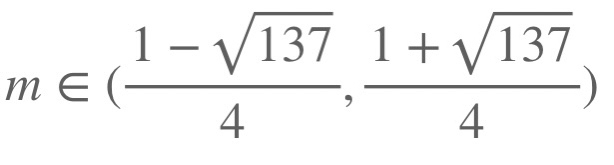ovavis19

Сегодня рассмотрим задачу интереснее и сложнее предыдущей. Условие выглядит так :

Дадим подумать некоторое время тем, кто сам хочет прорешать задачку!

А теперь начнем решать. Для начала заметим, что

Обозначим число цифр у числа n как p(n). Тогда из нашего неравенства мы сразу замечаем, что

Дальше будем решать от противного. Предположим, что у первого числа в условии цифр больше, чем у второго. Но максимальное число, у которого ровно m, цифр есть 10^(m)-1. Таким образом мы получаем следующее:

Также легко увидеть следующее:

Отсюда мы получаем

С другой стороны

Итак, мы получили двойное неравенство.

Так как k>3n, число посередине явно натуральное. Отсюда сразу же следует

Итак, мы вышли на финишную прямую. Если n=0 или n=1, то наши числа содержат одинаковое число цифр. Если же n>1, то

Но с другой стороны

Во второй строчке я воспользовался биномом Ньютона. Заметим, что 1+3^n не делится на 8 для всех n>0.

Итак, мы пришли к противоречию, которое и завершает наше доказательство от противного! Теперь можно идти пить кофе!

Разберем еще одну легкую задачу. Итак, вот условия.

Перед тем как перейти к решению, сделаем небольшую паузу. Мем посвящается моему коту.

Итак, перейдем теперь к решению! Для начала докажем следующее неравенство:

Будем доказывать его с помощью индукции.

В одну сторону мы доказали, теперь в другую.

Итак, мы доказали наше неравенство по индукции. Заметим, что наше доказательство также остается верным и при k=n. Ну а раз так, то подставим это значение в наше неравенство!

Задача доказана, пора пить кофе!

Разберем сегодня довольно простую задачку. Ее условия вы можете видеть ниже.

Выдержим небольшую паузу для тех, кто хочет сам решить задачу.

Итак, давайте теперь разберем эту задачу. Начнем с того, что сложим эти два уравнения и преобразуем их.

В одной из строчек я прибавил двойку и вычел двойку, что сохраняет исходное уравнение.
Последнее уравнение выглядит очень интересно. Так как все переменные в уравнении у нас натуральные числа, то вычитание из них единицы либо оставляет их натуральным, либо превращает их в ноль. Произведение таких же чисел также оставляет их либо натуральными, либо превращает их в ноль. Значит, у нас уравнение следующего вида:

На картинке приведено сразу и решение такого уравнения, которое очевидно ( так как мы ищем решение в целых положительных числах + ноль). Разберем, что означают эти решения для нашего уравнения

Здесь для пункта б) я сразу выписал ответ, так как он отличается от пункта а) просто заменой пары (x,y) на (z,t).
Ну и последний случай оказывается очень простым.

Ну а на сегодня все! Задача решена, идеи пить кофе со спокойной душой.

Сегодня мы с вами попытаемся решить сложную задачку, которая предлагалась на Московской олимпиаде 1998 года.

Твой взгляд, когда кофе ещё не готов, а работать уже надо

Итак, все, кто хотел решить сам,наверняка уже решают, а мы продолжим.
Давайте посмотрим, какие остатки дают левая и правая часть при делении на 3 для этого составим табличку.

Тут можно сказать, что я пытаюсь схитрить. Ведь не факт, что любые степени будут давать такие же остатки. Ну хорошо. Разберёмся подробнее! Остатки от деления числа на 3 я буду обозначать как это же число с чертой сверху. Таким образом

А теперь заметим важное свойство! Остаток от произведения двух чисел есть остаток от произведения двух остатков.

Докажем этот факт и будем иметь все необходимое для доказательства задачи!
Если число a даёт остаток n при делении на 3, то его можно записать в виде a=3q+n. Аналогично, если b даёт остаток m, то b=3r+m. Перемножим a и b!

Итак, утверждение доказано. Тогда подтвердим нашу табличку!

Получается, что слева у нас всегда остаток 0+1=1, а справа либо 1 , либо 2. Но так как выражения равны, справа должен быть остаток 1. Следовательно, z - четное число.
Теперь разберёмся с остатками на 4!

Отсюда следует,что x тоже четное. Обозначим z=2n, x=2m. Наше уравнение можно переписать в следующем виде.

Таким образом, левая часть разлагается на множители. Но правая часть может делится только на числа вида 2^k. Значит, получаем следующее выражение

Но погодите! 3^m всегда нечетно, а правая часть четная, кроме случая, когда k=1. Значит, обязательно k=1. Отсюда получаем, что

Аналогично, правая часть - делители левой. Но у левой части у нас делители -степени тройки. Но в правой части два сомножителя различаются на 2. Это возможно только тогда, когда меньший из сомножителей - 1. Значить 2^(y-1)-1=1. Следовательно, y=2. Подставляя эти значения в решение системы уравнений, получаем, что n=1 и m=1. Значит z=x=2. Т.е. решениями являются Пифагоровы тройки и других решений нет! Задача решена и можно пить кофе!

Сегодня у нас простенькая задача, балла на 4 из 10. Условия выглядят следующим образом

Делаем небольшую паузу, пьём кофе, смотрим мем и начинаем решать.

Теперь можно и приступить к разбору.
Давайте разберёмся, какие остатки от деления на три может давать квадрат числа. Произвольное число даёт в остатке от деления на 3 либо 0, либо 1, либо 2. Такие числа соответственно можно записать в виде 3k, 3k+1 и 3k+2. Рассмотрим их квадраты.

Первый квадрат имеет остаток 0, а два оставшихся имеют остаток 1.
Отсюда следует, что x и y не могут одновременно давать остаток и 1 и 2 от деления на 3 ( иначе z имело бы в остатке 2, а это запрещено для квадрата, как мы увидели выше ). Следовательно, одно из этих чисел делится на 3.

Теперь поглядим на остатки от деления на 8. Произвольное число при делении на 8 даёт в остатке либо 0, либо 1, либо 2, либо 3 и тд до 8. Эти числа записываются как 8k, 8k+1, 8k+2, 8k+3 и тд до 8k+7.
Посмотрим на остатки их квадратов.

Так как z^2 не может давать в остатке что-то отличное от этих чисел, то приходим к выводу, что либо левая часть даёт в сумме остаток 1 ( а это значит, что одно из чисел делится на 8), либо оба числа дают в остатке по 4. В первом случае все очевидно, так как какое-то число делится на 3 да еще одно из них на 8. Значит произведение делится на 24 (а на 12 и подавно). Во втором случае, если глянем на табличку, заметим, что оба числа будут делится на 2. Значит их произведение делится на 3 и на 4 ( по 2 от каждого числа). Таким образом xy делится на 12. Задача решена!