Как понять матанализ и решать им задачи классической физики | Часть 2
Итак, продолжаем познавать матанализ в физике. Перед прочтением очень рекомендуется ознакомиться с первой частью, но если коротко, то тезисно напомню:
- Функция - зависимость одной величины от другой или других
- Производная отражает скорость роста функции, является отношением дифференциала функции к дифференциалу аргумента, сами дифференциалы - бесконечно малые приращения
- Интеграл является действием, обратным взятию производным, и в то же время является операцией суммирования бесконечно большого числа бесконечно малых величин
- Дифференциальное уравнение - уравнение в котором неизвестной является некоторая функция
Ну а теперь продолжаем
Поскольку мы с вами уже освоили диффуры, интегралы и производные, то сейчас сами по себе они нас интересовать не будут. Будем считать, что если уравнения у нас уже есть, то мы гарантировано можем решить задачу. Сейчас сделаем упор на то как составлять уравнения для задач
Общее правило довольно простое: нужно записать известные из физики формулы, которые могут что-то описывать в задаче, ограничения, при этом их должно быть достаточно для однозначного решения задачи, не больше, не меньше. Сходу может быть непонятно: а какие именно формулы подходят, какие такие ограничения надо задавать, как понять, что уравнений достаточно и так далее. Поэтому все эти моменты мы разберем, и разберем на примере, так будет понятнее
И для этого возьмем вот такую задачу:
Звучит задача, конечно, немного страшно. Но это только так кажется. Как я написал выше, нужно записать необходимые формулы и из них искать решение, и для удобства, будем делать это последовательно
И первая формула, что приходит в голову, - второй закон Ньютона для поршня. Действительно, здесь на поршень будет действовать куча всяких сил, под действием которых он будет как-то двигаться, а движение поршня нам как раз и надо описать. Помимо этого, понятно, что двигаться он может только вверх-вниз, поэтому и рассматривать движение стоит только в этом направлении (то есть в проекции на это направление, но об этом чуть дальше). Уже что-то вырисовывается:
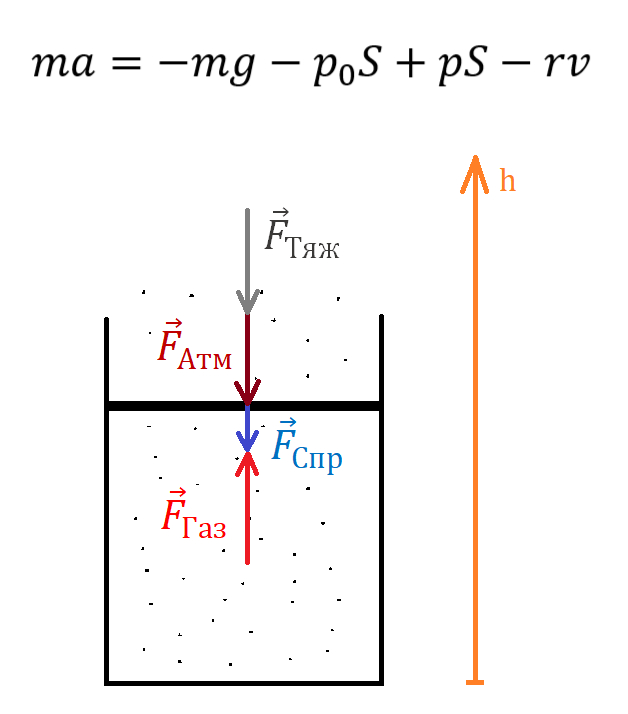
Теперь разберемся с силой, действующей на поршень (ну вернее силами, F в уравнении заменится на сумму сил). Поршень находится в поле тяжести, значит на него будет действовать сила тяжести. Также есть внешнее атмосферное давление, которое будет вдавливать поршень. С другой стороны, под поршнем же ведь газ, который тоже будет с какой-то силой его выталкивать. А еще при его движении будет возникать сопротивление. Вот эти 4 силы и будут вызвать движение поршня:
Теперь, как я думаю в уже поняли, нужно узнать, чему будет равна каждая из сил (очевидно, что для полного описания движения поршня нам будет достаточно определить все эти силы: тогда мы будем знать ускорение поршня в любом его положении и, соответственно, сможем из уравнения определить его движение). Ну с силой тяжести все просто, F = mg. С силами давлений (от атмосферы и от газа в сосуде) тоже все довольно понятно: давит и то, и то на поршень в каждой точке одинаково (так как газы однородны), поэтому можно воспользоваться простейшей формулой, связывающей давление и силу: F = pS. Сила сопротивления тоже не сложная, F = rv, в условии ж сказано. Так что слегка перезапишем наше уравнение, и перейдем к проекциям
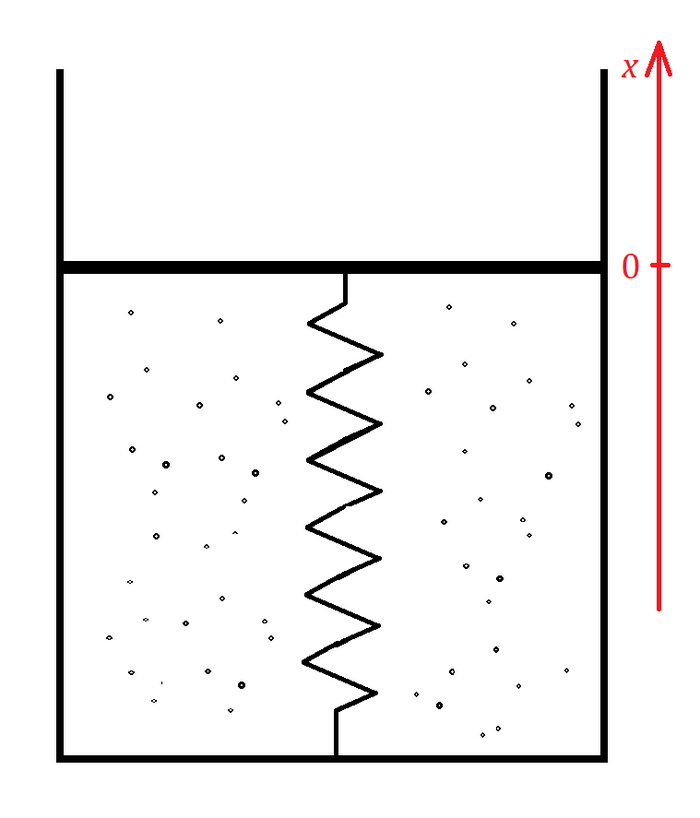
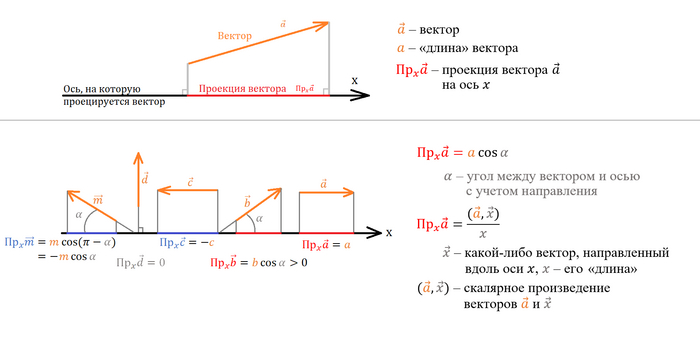
Оставлю примечание насчет проекций. Нам, понятное дело, работать с векторами очень неудобно, поэтому мы их переводим в обычные числа - проекции векторов. Сама по себе проекция получается при опускании перпендикуляров (на картинке ниже), но при этом ее прелесть в том, что она отражает направление вектора. Если он сонаправлен с тем, на что проецируем, то проекция будет положительна, противоположно направлен - отрицательно. Ну а если вектор находится под углом к тому, на что проецируем, то проекция будет меньше, чем длина этого вектора (если что, длина вектора силы равна числовому значению силы, то есть это не совсем привычная длина в метрах и сантиметрах). Короче вот:
Ускорение и скорость проецируются как сонаправленные с осью, на которую проецируем. Это объясняется тем, что проекции скорости и ускорения есть ни что иное, как производные координаты. Проверить довольно легко, просто сверяя знаки проекции и производной при различных направлениях вектора
Вернемся к нашим барашкам. В силе тяжести неизвестных нет, она нам сразу известна. В силе сопротивления есть скорость, но скорость определяется из самой диффуры (искомая функция в дифференциальном уравнении), поэтому ее мы оставляем так. С атмосферным давлением тоже все предельно просто: мы всегда знаем силу его давления, давление и площадь то нам даны) А вот с давлением газа в сосуде сейчас будем разбираться
Что приходит в голову в первую очередь, когда мы пытаемся описать газ? Уравнение идеального газа есестно. Поскольку цифры здесь не какие-то экстремальные, то оно будет вполне рабочим, поэтому им и будем пользоваться. Запишем его пока в уме) По условию, у нас еще газ теплоизолирован. Хм... Понятно, что нужно еще какое-то уравнение, которое будет описывать газ без теплообмена. А какое уравнение содержит в себе подводимое тепло? - Первое начало термодинамики, конечно. Из этих двух уравнений мы можем получить третье, уравнение адиабатного (без теплообмена то есть) процесса. Вот вывод, если кому интересно, вообще можно это уравнение и без вывода использовать:
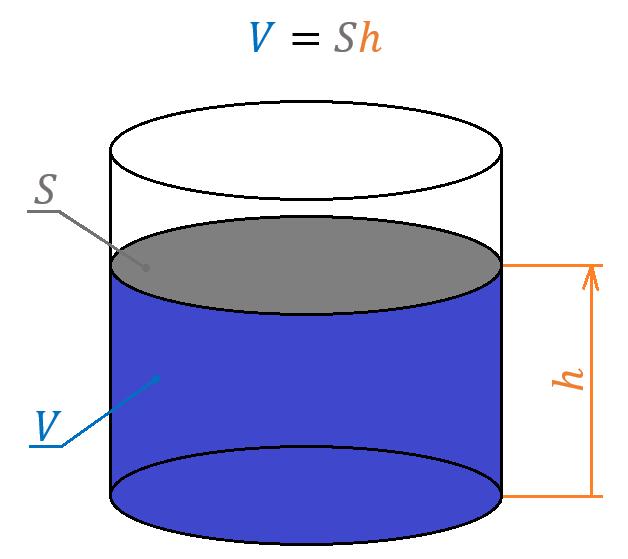
В нем у нас есть давление, объем и какая-то константа. Ну давление мы выразим, а что делать с объемом и константой? С объемом все просто, у нас ведь газ находится в цилиндре, значит, объем его – это площадь основания цилиндра на высоту. То есть на высоту поршня над дном. Снова неизвестная? А вот и нет, высота цилиндра определяет положение поршня, поэтому она у нас перестанет быть неизвестной при совокуплении с первым уравнением (вторым законом Ньютона, оно ж ведь и будет описывать положение и движение поршня):
Ну а что касается константы - какой момент времени мы бы ни выбрали, константа останется константой. То есть, она равна давлению с объемом и в какой-то произвольный момент, и в начальный. А значит мы ее просто напросто заменим на давление и объем в положении равновесия (для них ведь это тоже выполняется). А как посчитать давление в положении равновесия - тоже все просто, у нас ведь поршень должен будет оставаться неподвижен, то есть понадобится еще одно уравнение, для движения, и тут опять таки подойдет 2 закон Ньютона, только в этот раз скорость и ускорение мы сразу занулим, а положение поршня будет таковым, каковым было изначально. Возьмем уже выведенный закон Ньютона и переделаем его под наши нужды, ну а потом запишем наконец силу давления:
У нас в неизвестных теперь остались только характеристики движения, а они определятся из дифференциального уравнения (2 закона Ньютона) Доведем до конца уравнение для поршня. Подставим найденные силы, заменим скорость и ускорение на производные координаты (за координату мы выбрали высоту поршня над дном) и получим, наконец, конечное уравнение:
Буквы h с точками - это как раз скорость и ускорение. Вспомните, как обозначаются производные по времени
И вот у нас получилось нужное нам дифференциальное уравнение. Добавляя к нему ограничения, то есть начальную высоту цилиндра (дана в условии, сумма высоты в равновесии и расстояния, на которое поршень подняли) и начальную скорость (по условию равна нулю), у нас будет достаточно всего для однозначного решения задачи (по сути, задача свелась к одному дифференциальному уравнению второго порядка, для него нужно два начальных условия, поэтому так).
Оставлю небольшое дополнение: количество ограничений, нужных для задачи мы определяем путем суммирования порядков старших производных функций. Например, было 2 диффура для функций x(t) и y(t) (сколько диффуров - столько и неизвестных функций), причем в общем в двух уравнениях мы встречаем старшие производные x'''(t) (3 порядка) и y''(t) (2 порядка). Тогда количество ограничений (начальных или граничных условий) будет равно 3 + 2 = 5.
Аналитическое решение данное уравнение имеет только при малых изменениях h (попробуйте решить самостоятельно, позже разберем этот вариант), поэтому сейчас воспользуемся численным моделированием и решим это уравнение при помощи Wolfram Mathematica

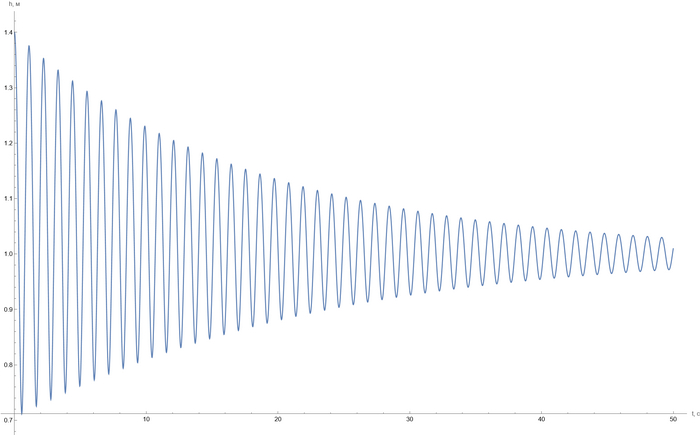
Код для численного моделирования и график функции, полученной численным решением
Собсна, задача решена. Также оставлю в виде картинки ее полное решение, вдруг кому так удобнее:
А, ну и еще кое-что красивое - анимация данного процесса (выполнена кстати тоже в Wolfram-е, цилиндр если что серый, а поршень оранжевый):
Выше я упоминал про случай с малым отклонением от положения равновесия. Давайте рассмотрим его (а после поймем, почему это так важно)
Что означает малое отклонение, думаю понятно: поршень колеблется очень близко к положению равновесия. Иными словами, если мы из функции h вычтем h0 (которое соответствует положению равновесия), то полученная величина (она и будет являться отклонением от положения равновесия) будет значительно меньше, чем h или h0
Но что нам дает этот факт? Разность h и h0 значительно меньше самих h и h0, а значит разделив разность на, например, h0, мы получим очень маленькое число, и такая функция может с достаточно высокой точностью считаться бесконечно малой, и к ней можно применять формулы для этих самых бесконечно малых (например, зануление величин более высокого порядка малости для дифференциалов, если забыли, гляньте первую часть :) ). А они позволяют очень удобно преобразовывать уравнения, и сейчас мы как раз на это посмотрим (хотя я выше уже проспойлерил, что для них мы получим аналитическое решение диффуры)
Как я уже сказал, мы будем использовать формулы для бесконечно малых, так давайте сперва эту бесконечно малую получим. Как? Так уже же находили, вычтем h0 из h:

В последних двух строках мы получаем выражения, которые подставим вместо h
Сама новая функция x не будет являться бесконечно малой. В принципе, это и так понятно, абзацем выше написал, но на всякий случай. Вернемся к задаче и преобразуем дифференциальное уравнение с учетом того, что x/h0 - бесконечно малая:
Что мы видим? - А мы видим линейное дифференциальное уравнение с постоянными коэффициентами, которое крайне легко решается аналитически (надеюсь, все хотя бы краем глаза глянули, как это делается :)?):
Попробуйте на досуге доказать, что решение второй вариант решения (только с косинусом) тоже является решением (делается несложно, подстановкой). Более интересный вариант - доказать что эта же форма является общим решением диффура
А что, собственно, примечательного? Да то, что в этой довольно сложной задаче мы смогли получить ответ не численным моделированием, а в виде формул. То есть мы получили результат не только для конкретных условий, которые заданы в задаче, а вообще для всех возможных, лишь бы начально отклонение было маленьким (кстати, интересный факт, для любых колебаний с малым отклонением от положения равновесия мы можем получить аналитическое решение, попробуйте доказать это на досуге). Да, это решение, конечно, приближенное. Однако оно все же довольно точное, и помимо того, позволяет гораздо лучше исследовать то или иное физическое явление
И обращу внимание, почему это важно. Да, здесь диффур компьютер решает довольно быстро. Но и диффур у нас всего один и только лишь от времени. Попадись нам 3-мерная, да еще и нестационарная задача (речь про диффуры в частных производных), и решение бы мы ждали довольно долго, к тому же такое решение само по себе не получится толком проанализировать. Поэтому в практических задачах важно уметь находить, подбирать какие-либо приближения, которые позволят хотя бы часть задачи из численного решения перевести в аналитическое
Ну а кому интересно удостовериться в точности, вот различие между численным и приближенным аналитическим решениями, вот графики:
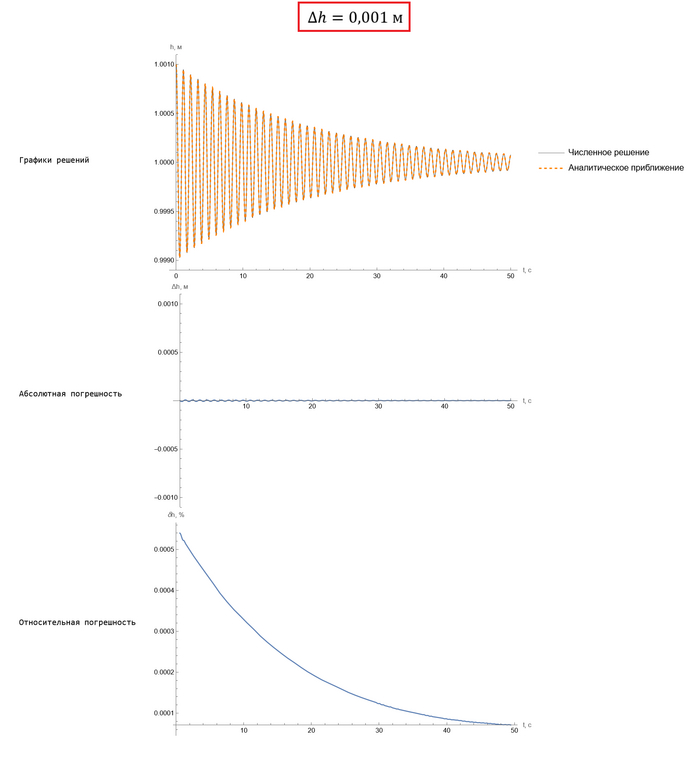
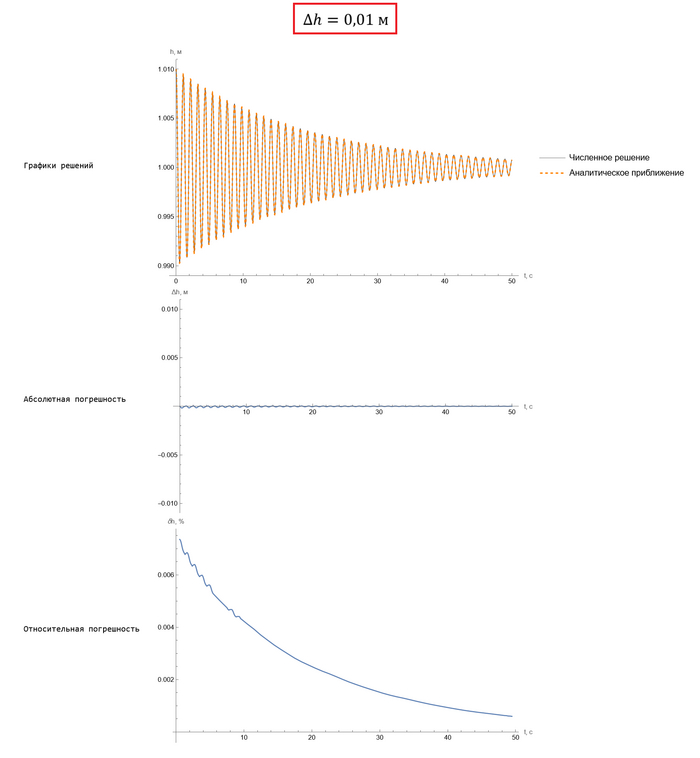
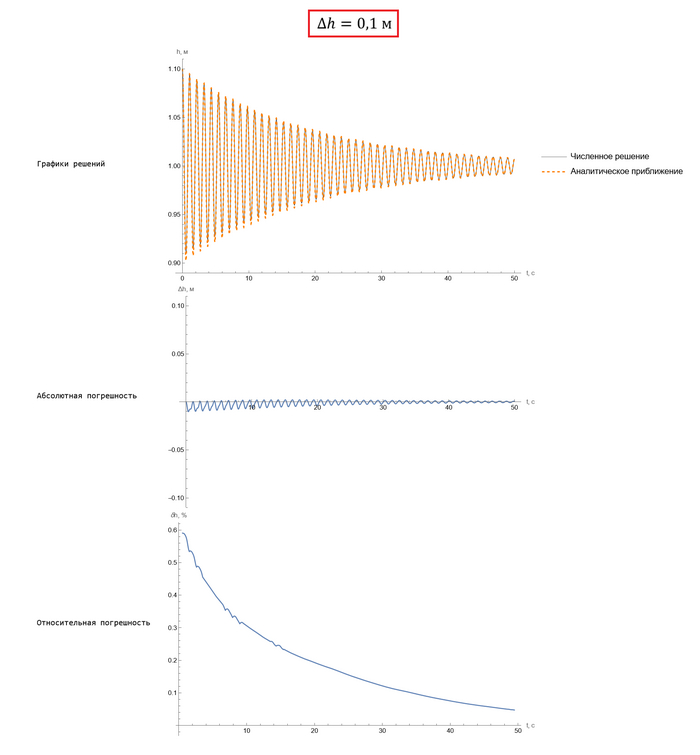
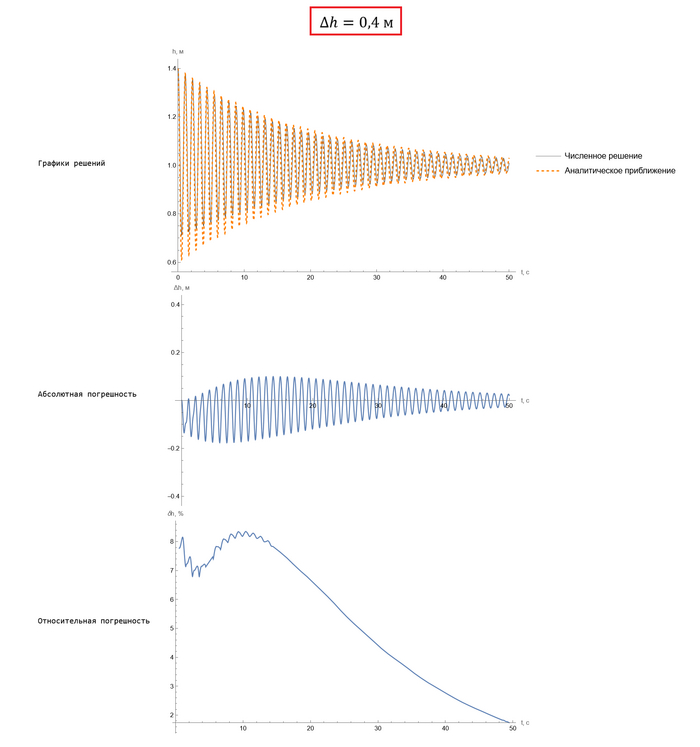
Обратите внимание: даже для нашей изначальной задачи, где отклонение от положения равновесия довольно большое, погрешность составляет не более 10%. Ну а для случаев, где отклонение действительно мало, и того меньше: не более сотой процента. Это, в общем-то, довольно хорошая точность
Ну и приведу еще полное решение картинкой (опять таки, вдруг кому так удобнее):
Что ж, на этом можно закончить мучать поршень с цилиндром) Но я попрошу вас здесь сделать паузу и пробежаться глазами по решению. Обратите внимание на подход: мы сперва записали одно из уравнений, которое должно будет что-то описывать в задаче (закон Ньютона), расписали его для случая в данной задаче. В результате у нас появился ряд дополнительных неизвестных, которые мы последовательно определяли, используя еще какие-либо формулы (сперва раскрыли каждую из сил, затем, так как у нас получилось неизвестным давление, записали формулы для газа, из них нашли давление и подставили в уравнение, и когда неизвестные в уравнении кончились, решили само уравнение). А при рассмотрении малых отклонений - внесли этот факт в уравнение. Думаю, осмысление и понимание этого принципа (записали формулу(-ы) и последовательно избавляемся от неизвестных в ней (них) при помощи других формул) позволит преодолеть такую проблему, как "не понятно, с чего вообще начинать решение". Хотя, конечно, тут еще будет важен опыт, то есть надо понарешивать задачек
Естественно, последовательно записывать и изменять уравнения - не единственный подход. Мы можем рассматривать бесконечно малый элемент какого-то процесса, также возможен вариант, когда мы записываем сразу все исходные уравнения и потом уточняем и редуцируем к более простой (в соответствии с условием). Но о них как-нибудь в другой раз...
Ну а на этом пост подходит к концу. Надеюсь, мне удалось изложить тему понятно, но если остались какие-то вопросы, то смело задавайте их в комментариях
Всем добра и аналитических решений!)


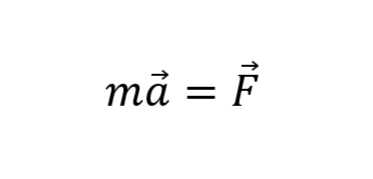



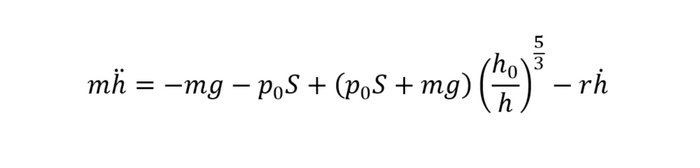




Наука | Научпоп
9.5K поста83K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.