Форма нашей планеты...3
Давно думал написать это в одном посте, т.к. в разное время попадались отдельные сообщения или комментарии на тему формы планеты (эллипс или геоид), а также рельефности поверхности. Такое ощущение, что люди даже близко не представляют себе реальность. Попробую это исправить...

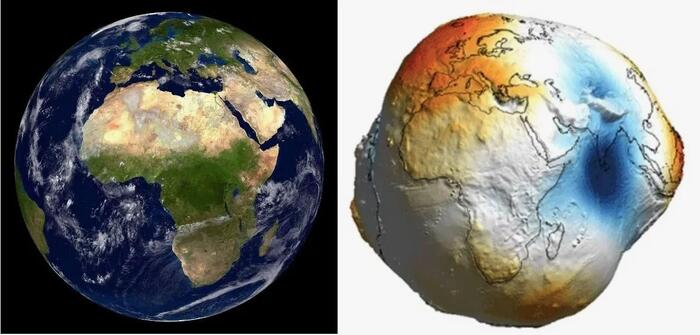
Я вот про эти дурацкие картинки, которая всем так понравилась...
Началось всё с того, что я решил купить ребёнку рельефный глобус или рельефную карту, которая наглядно показала бы причины выбора маршрутов переселения народов, военных походов и т.д.
Изучив предложенные варианты я понял, что на масштабах комнатных карт или глобусов горы получаются настолько утрированно огромными, что для их изображения значительно преувеличивается площадь подошвы горных массивов и некоторые регионы становятся горными вместо равнинных. Как наглядное пособие - неплохо, но как более-менее реалистичное отображение - вообще не то.
Такое положение меня немного не устроило и я решил попробовать самостоятельно изготовить глобус с реалистичным масштабом рельефа, ведь сейчас нет никакой сложности напечатать и раскрасить что угодно на 3D принтере. Взялся за анализ и понял, что занятие это почти бессмысленное. На масштабах глобуса в человеческий рост (2,0м в диаметре), глубина Марианской впадины получается 1,7мм.
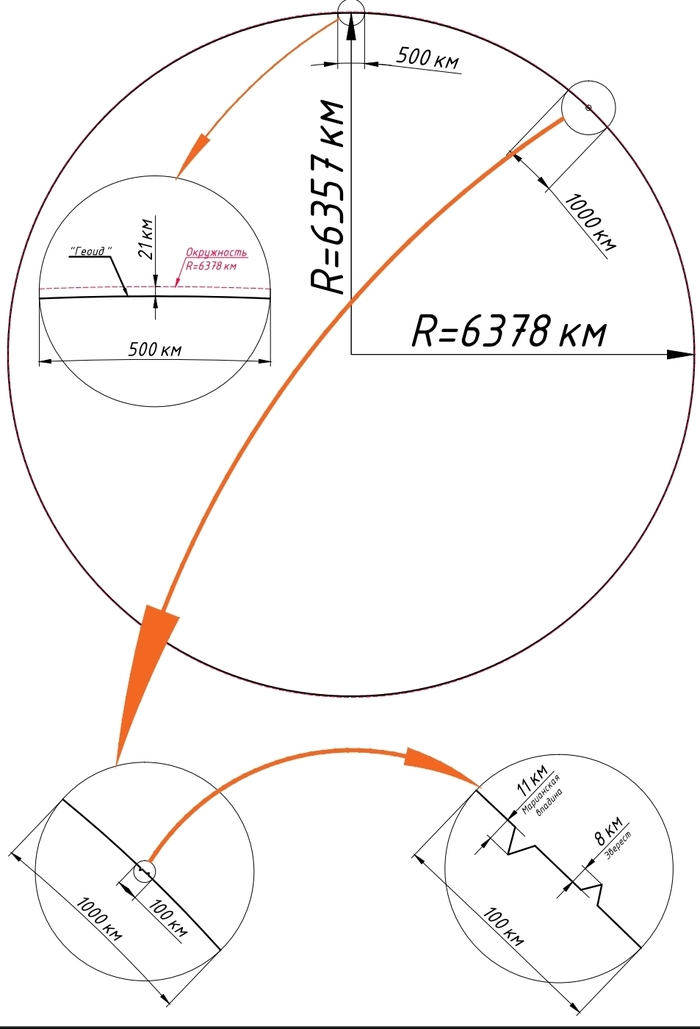
Что сподвигло меня прикинут вообще масштабы озвученных мифов про "не шарообразность" Земли, геоидную форму и т.д.. Нарисовал эллипс в миллиметрах с разными радиусами по вертикали и горизонтали, ожидая получит тот самый эллипс-геоид-овал...
Но по факту вышел круг с крошечной погрешностью в вертикальном и горизонтальном измерении - 0,2%.
Получается, что наша планета - совершенно идеальный шар с лёгкими шероховатостями в виде гор, каньонов, океанов...
В одном из обсуждений на эту тему я увидел аргумент, что "если разница диаметров есть, то, всё же, не шар". Ну, формально я согласен, действительно не шар. Но как можно понять это? Ведь на масштабах планеты это хоть как-то получается измерить, а как это измерить на понятных нам масштабах?
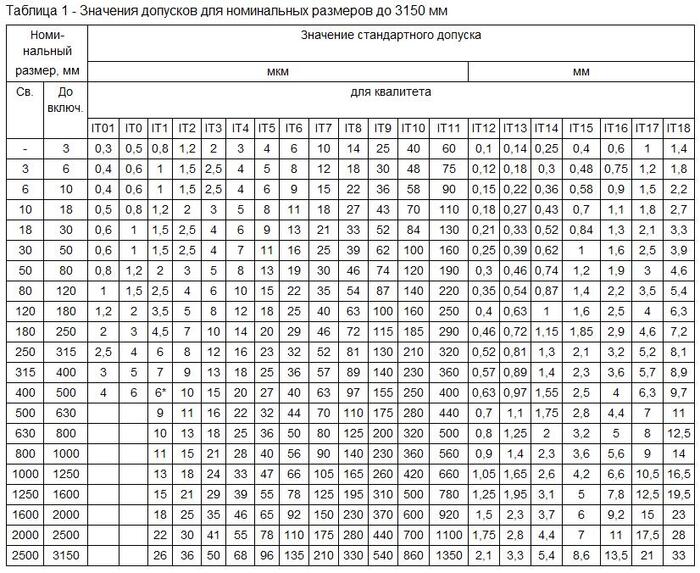
Есть такой ГОСТ 25346-2013 "Система допусков на линейные размеры. Основные положения, допуски, отклонения и посадки". Этот нормативный документ, в числе прочего, содержит таблицу допусков по квалитетам точности изготовления деталей разного назначения.
Таблица 1 из ГОСТ 25346-2013 "Система допусков на линейные размеры. Основные положения, допуски, отклонения и посадки"
Квалитет может быть разный, зависит он от требований к точности изготовления, а от квалитета зависит сложность изготовления, обработки детали и цена изготовления.
Квалитеты с 1 до 4-го используются для изготовления калибров и контркалибров.
Квалитеты от 5-го до 12-го применяют для изготовления деталей, образующих сопряжения (ГЦС).
Квалитеты от 13-го до 17-го используют для параметров деталей, не образующих сопряжений и не оказывающих определяющего влияния.
То есть, примерно на границе IT12-IT13 квалитета находится разница между машиностроительными требованиями к деталям для механизмов и обычными требованиями к качеству изготовления деталей для строительства и конструирования. То есть, контроль качества изготовления не мелкой (20-30см) детали при квалитете IT12 или IT13 доступен и понятен большинству населения - линейка, штангенциркуль, а при квалитетах ниже IT12 это уже микрометр на калиброванных столах для измерения - доступно не всем.
Возьмём для понятного примера футбольный мяч. Его наверняка держали в руках почти все.
Так вот, диаметр футбольного мяча - 22см, то есть 220мм, а это значит, что согласно квалитету IT12, точность изготовления металлического шара колеблется от 0,18%(для 250мм) до 0,26%(для 180мм) от линейного размера, при диаметре 220мм, точность нормального изготовления металлического шара - 0,214% от линейного измерения, то есть 0,47мм.
Сможет ли кто-то из нас без инструментов, "на глаз", оценить шарообразность футбольного мяча, если разница в диаметрах будет 0,47мм? Я сомневаюсь. Но тут спорить особого смысла нет.
С футбольным мячом есть ещё один интересный пример для понимания масштабов рельефа нашей планеты. Мы же все, наверняка, держали его в руках. Все видели на нём швы. Вот эти швы и будут отличной иллюстрацией для ощущения рельефа нашей планеты.
Для простоты расчёта предположим, что глубина шва на поверхности мяча - 1мм.
Диаметр футбольного мяча - 22см или 220мм.
Диаметр планеты Земля (возьмём экваториальный радиус из Википедии) - 12 756,2км или 12 756 200 000мм.
То есть, диаметр планеты Земля в 57 982 727,3 раза больше диаметра футбольного мяча. А значит, если бы шов на футбольном мяче являлся бы масштабной моделью каньона на поверхности планеты, то на теле нашей планеты такой каньон должен был бы быть 57,98км глубиной.
Даже если я ошибся в допущении и шов на футбольном мяче глубиной не 1,0мм, а 0,5мм, то каньон всё равно получается глубиной 28,99км.
То есть, Марианская впадина (до 11 км глубиной), если её масштабно изображать на поверхности футбольного мяча, должна быть глубиной 0,18мм - то есть просто ЦАРАПИНА НА КОЖЕ МЯЧА.
Как-то так...





Лига упоротых расчетов
495 постов7K подписчиков
Правила сообщества
Лига занимается странными веселыми подсчетами на основании уже имеющихся в общем информационном доступе знаний. Расчеты - ради лулзов и хорошего настроения. Не нудите сами и не занудничайте в адрес других, играть в Шелдона Купера хорошо до определенного предела.