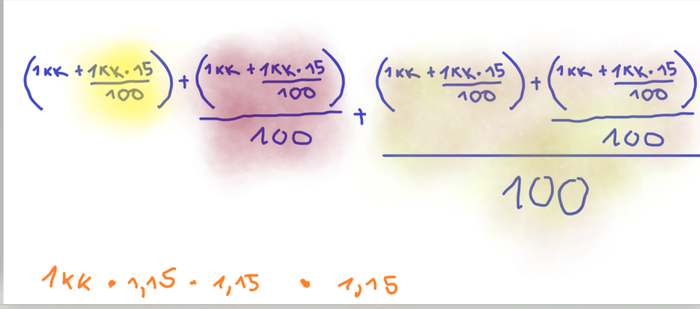Собственно концепция такая. Вместо пропорции мы новое значение получает умножением старого на одну целую хрен десятых (или ноль целых хрен десятых). Из плюсов - нам не нужно знать промежуточные результаты и тратить на их поиск силы. Мы можем считать сразу конечный результат. (причем любой промежуточный результат мы получить таки можем без каких либо сложностей если производим действия поочередно). Минус в том, что перестают использовать пропорции т.к. считать так тупо удобнее, но это уже не проблема самого подхода


*Маленькая вставка*
Понятное дело, что математически одна фигня что пропорции, что метод использования аля сложный процент. Абсолютно те же яйца, только в профиль, но удобнее жамкать. Это я вам как репетитор говорю.
*Конец маленькой вставки*


То бишь. Увеличилась стоимость куртки с 4000 на 15%  и финальная стоимость тогда становится равной x= 4000(1+15/100) = 4000*1.15 = 40*115 = 4600.

Либо та же ситуация но уменьшение на процент. Та же куртка в 4000, но цена снизилась на 15%. Итого x= 4000*(1-15/100)=4000*(1-0.15)=4000*0.85 = 40 * 85 = 3400


Почему так удобнее чем через пропорцию?
Потому, что на каждую такую операцию нужно делать свою пропорцию.
Скажем хочу я узнать сколько будет стоить курта после увеличения цены на 15%, затем на 10, затем уменьшение на 20, затем увеличение на 40, затем снижения на 10 и с условием подхода аля "формулы сложного процента" мне придется сделать всего лишь следующее:

4000*1.15*1.10*0.80*1.40*0.90
Далее значение легко считается на калькуляторе или ручками

При пропорциональном способе вам придется делать 5 пропорций, в которых на каждом этапе можно очень легко запутаться. Но это еще цветочки.

Попробуйте просто записать в виде пропорций  расчет  капитализации процентов при ставке в 15% на 10 лет.  Предположим, что мы идем простым путем и сразу фигачим общую формулу без шагов. Тогда мы получим:

И это методом пропорций в сокращенном формульном виде за 3 (!) года.
Желтым подсветил сумму которая добавилась по завершению первого года, красным после 2ого и т.д.  Я вот не возьмусь даже написать форумулу за 10 лет.

Ниже то же самое за те же три года (специально не стал писать полную формулу сложного процента дабы не вводить никого в заблуждение, а сделал простую версию этой же формулы), но  якобы "новым методом" (хотя он древний настолько же насколько и пропорции). Точнее производной от него. Разница явно видна.

Проблема в том, что запоминают дети именно пропорцию, как очень легкий и удобный инструмент работы в простых случаях с процентами, а потом пихают его везде где это нужно и можно использовать (как в вашей задаче) так и туда где это не очень разумно (как в примере с капитализацией).


Но!

Это
1) не дает право снижать оценку т.к. в задаче не указано каким способом надо решить, а значит нужно решить любым (кроме случаев совсем уж сумасшедших вычислений когда умножение к примеру 20*40 проводится в виде 20+20+20....(40 раз).

2)В вашем случае даже быстрее и проще сделать пропорцией (более того сам бы делал тоже по вашему же решению ибо оно вполне себе может произведено быть в уме или в одну строчку на бумаге, а предложенное учителем предлагает делить на дробь, что интуитивно сложнее).

3) Если они проходят тему со сложными операциями с процентами на данный момент (то бишь задание в учебнике относится к этой теме) , то учитель имеет право сказать "временно забыли о пропорциях и делаем только новым способом". И тыкать оценки на свое усмотрение.

Но[2]!
1) Есть учителя своевольные и упертые. Но профи. Нацеленные на результат итоговый. Особенно если ведет математику не педагог, а математик. В таком случае оценки стоит принять и сделать выводы. Какой в вашем случае учитель - фиг его знает, но позиция такая имеет место быть.

2) В вузе будет обращать внимание на самое элегантное решение. В подавляющем большинстве случаев это решение не пропорция.


Однако, это всего лишь имхо.

И печально в комментариях видеть «Данные задачи необходимо решать не для того, что бы получить правильный результат» или «На уроке прошли тему - задали домашнее задание по уроку, будьте добры делать так как нужно». Теряется смысл самого образования, особенно, замечу, если учитель НЕ объяснял, как в случае с ТС. Почему родитель должен изучать новые способы решения?! Откуда ему взять на это время, ведь ещё надо русский, лит-ру, английский, а родитель в школе учил немецкий. Быть может учитель должен записать видео с объяснением материала?! Да ну, не, бред какой-то. Для общества дисциплинированных дураков, конечно такой подход гораздо полезнее. Вот только напрочь убивает желание искать решение проблемы/задачи/вставьте нужное. Креативность на нуле, не думает, не решает. Меня такое не устраивает. И ТС, я вас прекрасно понимаю, для меня тоже важнее решить поставленную задачу и пофиг каким способом я это сделаю, хоть на кобыле задом наперед.

Соответственно мы решили её так:
х = 100 %
60 = 3 %
х = 60*100%/3% = 20*100 = 2000
Причем тут очень удобно сокращается 60 на 3 и задача решается легко и быстро.
Я очень люблю метод пропорции еще и потому, что ребенку иногда бывает сложно сообразить, когда нужно делить, а когда умножать, а при составлении пропорции сразу всё становится понятно.
В итоге сыну поставили за эту тему трояк. И это при том, что решение и ответы верные.
В разговоре по телефону учитель математики сказала мне, что решено, конечно, все правильно, но почему-то "устаревшим методом пропорций". Я ответила, что это моя вина, я сыну так объясняла, потому что так учили нас. Но ей нужно было решение "более современным методом", о котором мы должны были прочитать в учебнике. Поскольку этого решения она не увидела, то сочла возможным снизить отметку.
Спорить я не стала, потому что школьные оценки для меня давно не имеют значения. Но меня волнует другое. С каких это пор вдруг верные математические методы стали устаревать? Ведь математика точная наука, к ней не применимы такие суждения. И почему вдруг метод, выбранный учителем, лучше метода, выбранного мной? В наше время, если ученик решал что-то не так, как показал учитель, его хвалили за это, а не наказывали... И очень часто учителя ставили хорошую оценку, несмотря на то, что решение не было доведено до конца, если видели, что ход этого решения верен. Что вдруг могло произойти такого в математике, что за верное решение, но не тем методом, можно снижать оценку даже не на бал, а на целых два? И ладно, если это происходит, как у нас произошло, но я не хочу, чтоб, например, поступление наших детей в ВУЗ зависело от того, что вдруг в голову учителю, принимающему экзамен, взбредет, что ему не нравится метод решения пропорцией, или любой другой правильный метод решения, лишь потому, что он предпочитает "более современные методы"...
И кстати, оказалось, что этот более современный метод заключался в том, что нужно сначала перевести процент в десятичную дробь, а потом поделить на нее данное число:
3 % = 0,03
60 / 0,03 = 6000/3 = 2000
Я, может, чего-то не понимаю, но, на мой взгляд, поделить 60 на 3 и умножить на 100 гораздо проще для ребенка, чем соображать, как там поделить 60 на 0,03...
А по сути эти два действия вообще противоречат друг другу... Сначала 3 разделили на 100, а потом обратно умножили, ведь если правильно все расписать, то получится:
3 % / 100 % = 0,03
60 / 0,03 = (60*100)/(0,03*100) = 60 * 100 / 3 - а ведь это и есть наш метод решения: 60*100 % / 3 %
В итоге получается полный бред, лишние манипуляции для ребенка и запутывание мозгов.
Вот такая вот она современная математика, бессмысленная и беспощадная!
Ну и пруфы, конечно.

А раньше я думала, что вот это - верх издевательства над математикой:

Эх, как же я ошибалась!