Довольно часто в комментариях и постах, как на Пикабу, так и в других местах, я наблюдаю как людям бывает сложно понять, как именно работают вероятности на больших числах. Не формулы или теоремы, а на прикладном уровне, в формате "а когда мне повезет?" так сказать.
Это нормальное явление. Многие люди редко применяют математику сложнее таблицы умножения после школы или универов, а мозг устроен так, что легко забывает то, что не практикуется.
И это успешно эксплуатируют всевозможные лотереи и их подобия. И если чистые лотереи остаются в большинстве своём уделом бабушек с почты россии, то Морковск зацепил куда бОльшие слои населения, просто потому что а) идет как бы бонусом к обычным покупкам, б) озоном пользуются очень многие.
На примере недавно обновленной акции Морковска, попробую объяснить на пальцах, как здесь работает вероятность, математическое ожидание, отклонения и прочие штуки, звучащие сложно, но на деле - довольно естественно понимаемые при практическом применении. Я специально не буду писать формулы и рисовать графики. Кто знает - тот и так из знает. А кто не знает - тому картинка колокола Гаусса ничего не объяснит. Всё-таки теория вероятностей - это целый большой раздел математики.
ДЛЛ: Половина играющих людей через 7 лет регулярной игры при тратах на покупки 4000 рублей в неделю, так и не увидит выигрыш хотя бы 3000 рублей, но будет получать регулярные возвраты морковок и призы 25-150 рублей.
Теперь посчитаем подробнее.
(Я не буду касаться вопросов "подкрутки, нечестной игры, подставных игроков" и прочей недоказуемой спекуляции. В этом посте про математику.)
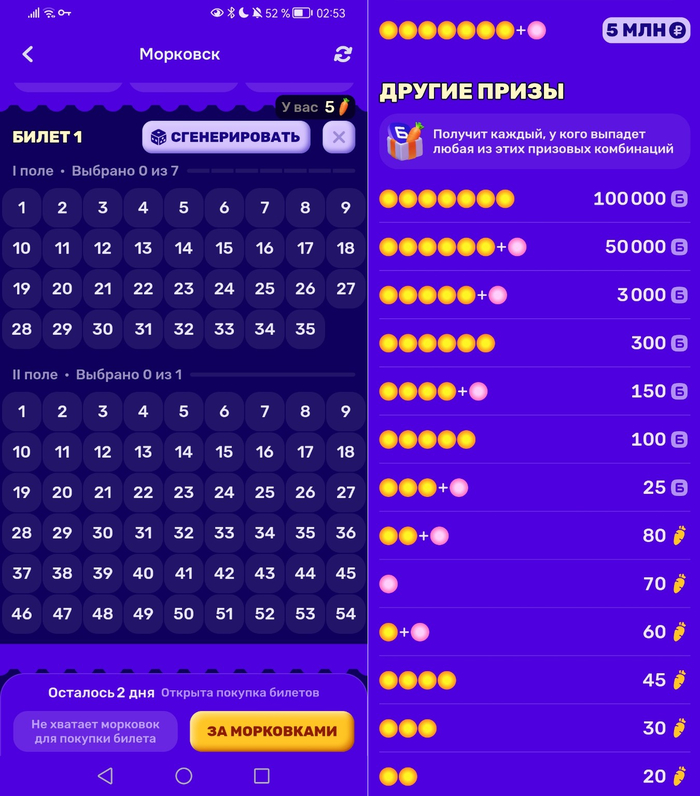
Для начала посчитаем вероятности. Нам предлагается на каждый билет заполнить два поля. В одном выбрать 7 цифр из 35 (желтые шары), во втором 1 из 54 (розовый шар). Итого 8 цифр. Организатор два раза в неделю "крутит барабан", получает 7+1 цифру и сравнивает их со всеми билетами на определенные призовые совпадения.
Даже не зная формулы, логически понятно, что вероятность угадать все 8 цифр сильно меньше, чем попасть в 3 или 4. Не грузя расчётами, примерно вот настолько меньше:
7 желтых + розовый (5 млн ₽) Джекпот ≈ 2.75e-9, это примерно 1 к 363 000 000
7 желтых (100 000 ₽) ≈ 1.46e-7, примерно 1 к 6 850 000
6 желтых + розовый (50 000 ₽) ≈ 5.40e-7, примерно 1 к 1 850 000
5 желтых + розовый (3 000 ₽) ≈ 2.19e-5, примерно 1 к 45 700
6 желтых (300 ₽) ≈ 2.86e-5, примерно 1 к 35 000
4 желтых + розовый (150 ₽) ≈ 3.16e-4, примерно 1 к 3 170
5 желтых (100 ₽) ≈ 0.00116,примерно 1 к 863
3 желтых + розовый (25 ₽) ≈ 0.00197, примерно 1 к 507
2 желтых + розовый (80 морковок) ≈ 0.00568, примерно 1 к 176
1 розовый (70 морковок) ≈ 0.00326, примерно 1 к 307
1 желтый + розовый (60 морковок) ≈ 0.00726, примерно 1 к 138
4 желтых (45 морковок) ≈ 0.0167, примерно 1 к 60
3 желтых (30 морковок) ≈ 0.1046, примерно 1 к 9.6
2 желтых (20 морковок) ≈ 0.301, примерно 1 к 3.3
1 к 3.3 звучит просто, понятно и очевидно, что-то вроде "почти каждый третий билет будет возвращать 20 морковок". 1 к 363 миллионам звучит в целом тоже понятно, что-то вроде "никогда-никогда за сто жизней никогда".
Но попробуем превратить это в конкретное время для выигрыша какой-то более менее существенной суммы. Пусть интересуемая сумма будет 3000 рублей и выше (то есть больше 300 - предыдущего приза), то есть первые 4 призовые строчки. Вероятность этого события (просто суммируем) получается примерно 1 к 44 000. Теперь привяжем ко времени.
Розыгрыши проводятся 2 раза в неделю. Если бы мы получали по одному билету на каждый розыгрыш, логично, это заняло бы около 22 000 недель. То есть среднее время ожидания примерно 423 года. И это именно среднее, не гарантия.
Для более наглядного представления, можно посчитать не среднее время, а медианное. Не вдаваясь в детали формул: среднее в данном случае отвечает на вопрос "сколько ждать в среднем по больнице", а медианное отвечает на вопрос "через сколько времени у половины таких людей уже что-то случится, а у половины еще нет". Так вот для такого случая ответ звучит как "При использовании одного билета на каждый розыгрыш, даже через 293 года у половины таких людей не будет выигрыша больше 300 рублей."
Но у нас же много билетов!
Представим, что мы тратим 4000 рублей в неделю на покупки на Озон. Из них примерно половину покупок стараемся попадать в акции морковок типа "купи определенный бренд на 300-500 рублей, получи 900 морковок". Это примерно 1 морковка за потраченные 50 копеек. И это значительно выгоднее, чем обычный курс начисления: 15 морковок за каждые 300 потраченных рублей, т.е. 1 морковка за 20 рублей покупок. Примерно в 40 раз выгоднее.
К слову, именно эта механика является ключевой в этой рекламной компании, т.к. в этом месте у людей начинает работать логика "возьму этот бренд, а не тот, потому что так я повышу свои шансы выиграть".
Итак, мы тратим 4000 в неделю, из них примерно 2000 на обычные покупки, вторую 2000 на акционные. Получаем примерно 88 билетов в неделю, или 44 билета на один розыгрыш.
Учитывая вероятность получить приз больше 300 рублей равную 1 к 44000 (как посчитали выше), получаем среднее время (матожидание) для таких условий: 500 недель или всего-то 9.6 года. Среднее медианное, для наглядности, составит 6.6 года за счет отброса длинных хвостов.
Или, говоря простым бытовым языком:
Половина таких игроков не увидит ни одного выигрыша выше 300 руб. даже за 6-7 лет.
Кто-то выиграет через месяц или два, такие истории будут, они статистически неизбежны, но это так называемые положительные хвосты - чистая левая часть распределения, очень редкая.
За 1 год такой еженедельной регулярной игры на 44 билета в каждый розыгрыш, призы выше 300 руб. получит только 1 из 10 таких людей (10-й перцентиль).
Каждый четвёртый такой человек увидит такой выигрыш раньше, чем через 2.8 года (25-й перцентиль).
Но 10% игроков не получат такой выигрыш даже спустя 22 года (90-й перцентиль).
Теперь вся шкала для таких условий целиком, чтобы было проще представить:
Какой вывод, спросите вы? Довольно неожиданный. Вывод заключается в том, что при таких больших числах, даже увеличение шансов в 44 раза - не приближает время выигрыша в адекватные масштабы. 44 билета два раза в неделю звучит как "много", в голове это звучит почти как гарантия, но на самом деле ты просто ускоряешь время, не меняя масштаб вероятностей.
Это похоже на то, как если бы человек говорил: "Я же не один раз кидаю монетку, а сорок четыре раза." Но если это такая монетка, которая выпадает орлом один раз за 40 тысяч бросков, то сорок четыре броска почти ничего не меняют.
При этом, мелкие денежные выигрыши (100-300 ₽) будут случаться регулярно, раз в несколько недель, и они создают ощущение, что система работает и что-то иногда отдает, и мозг начинает автоматически экстраполировать это чувство на большие суммы, хотя математически между ними пропасть.
Итого короткий вывод: Нет объективного смысла покупать акционные товары для дополнительных морковок, т.к. хоть это и сократит среднее время выигрыша значимых сумм, но сокращение произойдет с 400 лет до 10 лет, что всё еще значительно превышает адекватное время с любых точек зрения.
UPD. Пост начинал писать примерно неделю назад, и с тех пор Озон немного изменил мелкие награды, заменил 25 баллов на 50, добавил 20 и 30 баллов вместо морковок и прочие мелочи. Но общие вероятности и расчёты для призов выше 300 рублей остаются верными.