Бесконечный отель Гилберта: как разместить бесконечное количество гостей⁠⁠

Введение: Что такое отель Гилберта?

Отель, у которого нет конца. Не просто очень много номеров, а бесконечное их количество — номера пронумерованы числами 1, 2, 3 и так далее, без остановки. Это не реальное здание, а мысленный эксперимент, придуманный немецким математиком Давидом Гилбертом, чтобы показать, как работает бесконечность. В обычной жизни, если отель заполнен, новых гостей разместить нельзя. Но в мире бесконечности правила меняются, и отель Гилберта тому отличный пример.

Часть 1: Заселение одного гостя

Давайте представим такую ситуацию. В отель приходит новый гость, Дмитрий Анатольевич, с чемоданом в руке. Он вежливо спрашивает: «Есть ли у вас свободный номер?» Казалось бы, в отеле с бесконечными номерами найдётся один не занятый. Проблема в том, что в данный момент в отеле проживает бесконечное количество гостей. Одна бесконечность полностью заполнила другую. Но управляющий улыбается и говорит: «На самом деле есть один способ, чтобы вас заселить, но для этого придётся побеспокоить всех гостей отеля».

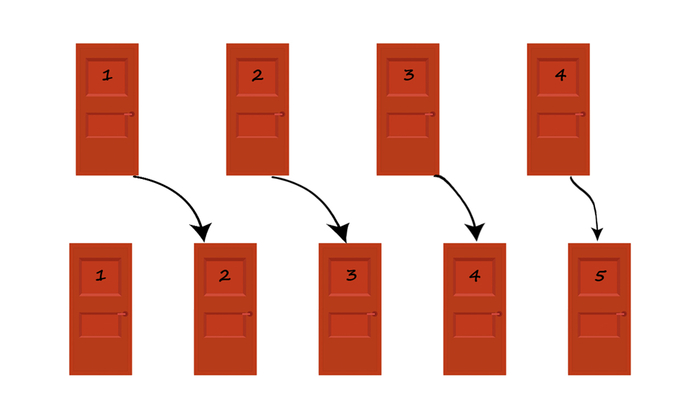
Управляющий придумал хитрый план. Он объявляет по громкой связи: «Дорогие гости, пожалуйста, прибавьте к номеру своей комнаты единицу и заселитесь в комнату с таким номером». Гость из номера 1 переезжает в номер 2, из номера 2 — в номер 3, из номера 3 — в номер 4, и так далее до бесконечности. Поскольку номеров бесконечно много, каждый гость найдет себе новое место, а номер 1 освободится. Новый гость с радостью заселяется, написав имя, фамилию и номер телефона в регистрационную книгу.

Не успел отойти от стойки, как новому жильцу звонит его старый знакомый, допустим, Пётр Александрович, и интересуется, как он заселился. В конце телефонного разговора он упомянул, что через час подъедет автобус с его друзьями. «Это ведь не проблема?» – спросил Дмитрий Анатольевич. «Смотря сколько их», — спросил управляющий. «Количество друзей Петра Александровича не имеет границ, заселили меня, заселите и их».

Часть 2: Бесконечное количество друзей

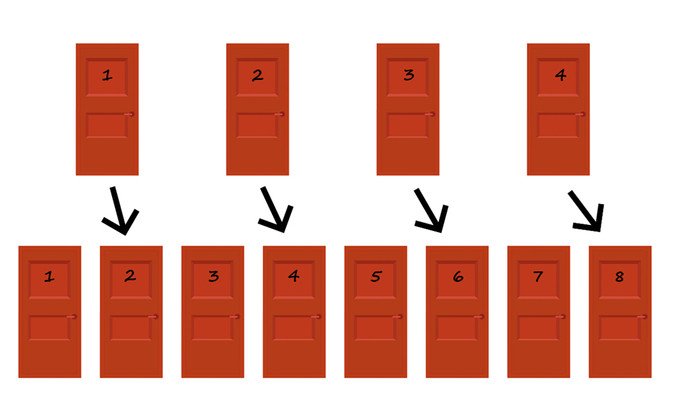
Теперь задача усложняется: нужно объединить две бесконечности. Управляющий отелем решает её с помощью математического трюка. «Дорогие гости, — объявляет он, — пожалуйста, умножьте номер своей комнаты на два и заселитесь в комнату с таким номером». Гость из номера 1 переезжает в номер 2, из номера 2 — в номер 4, из номера 3 — в номер 6 и так далее.

Что происходит? Все текущие гости занимают четные номера (2, 4, 6, 8...), а нечетные номера (1, 3, 5, 7...) остаются свободными. А поскольку нечетных чисел тоже бесконечно много, все друзья уважаемого Петра Александровича могут заселиться в эти номера. Бесконечность плюс бесконечность? В отеле Гилберта это не проблема!

Часть 3: Не бесконечные номера телефонов

Однако есть один момент, который меня беспокоит: если у новых гостей номера телефонов представляют собой бесконечные комбинации цифр, это ставит меня в затруднительное положение, так как я уверен, что не смогу разместить всех вас.

«Но как же так?» – спросил гость. «Вы только что заселили меня и друзей Петра Анатольевича, какая разница, какие у них номера телефонов?» Я объясню.

Давайте составим список из 10 случайных телефонных номеров. В этом списке мы выделим первую цифру первого номера, затем вторую, третью и так далее.

Чтобы сделать каждый номер уникальным, мы добавим к каждой цифре в этой последовательности единицу, а девятку заменим на ноль. В результате у нас получится новый номер. Сколько бы номеров мы ни добавляли в список, я всегда смогу найти уникальный номер, который будет отличаться от остальных как минимум на одну цифру.

Поскольку у Петра Александровича много друзей, ваш номер телефона обязательно будет среди них. Выбирайте: либо я заселю вас, либо всех, но один из них точно останется снаружи, и, возможно, это будете вы.

Часть 4: Подведём итог

Гранд-отель наглядно демонстрирует удивительное свойство бесконечности: даже если отель имеет бесконечное количество комнат, в нём не всегда может найтись место для новых гостей.

Спасибо, что прочитали мою статью. Для меня это был, что называется, первый опыт. Поэтому критика приветствуется)