Ищу книги по математике
Здравствуйте!
Мне 31 годик. Математику в школе и ВУЗе учил хорошо и прекрасно сдавал экзамены по ней. НО
К сожалению, в повседневной жизни, после окончания ВУЗа, математика (в общем смысле) мне пока не понадобилась. Это привело к тому, что я просто-напросто все забыл.
Я не забыл как в уме умножать и делить, но все алгебраические выражения, которые были написаны на моей линейке, ушли в закат за ненадобностью.
На данный момент, я понимаю, что тупею. Особенно, когда вижу абсолютно любой математический пример в книжке. Мой мозг просто отказывается считать что-либо.
Работа моя к математическим расчетам не располагает. Необходим толчок моему мозгу.
Есть желание изучать статистику, криптографию, теорию вероятности и т.д.
Теперь к делу. Может кто знает толковую книжку по математике, в которой шаг за шагом я могу вспомнить все то, что я когда-то знал, включая высшую математику на уровне нематематематического ВУЗа? Желательно ещё и с каким-нибудь сборником задач.
Поиск по Пикабу, как обычно ничего не дал.
Где же найти конечное зло?
Первое и что самое главное следует сказать о зле и добре - это то, что для начала эти вещи просто относительны. Для кого-то что-то может являться добром, в то время как для другого это будет злом. Две противоборствующие стороны также по определению друг для друга являются злыми, в то время как каждый для себя является добром, что особенно ярко можно наблюдать в политике. И для того, чтобы проявить в такой ситуации трезвое здравомыслие, адекватность, дальнозоркость и пр. человеку надо уметь мыслить поверх неё, уметь взглянуть на неё со стороны и уметь рассуждать нейтрально, отстранёно, с максимум непредвзятости и честностью перед самим собой прежде всего, ища гольную истину. Ну и дальше уже каждый для себя действует по ситуации, только уже и более осознанно.
Но это всё локально. А что если попробовать поговорить об этом глобально? Ведь там как раз и нет возможности выйти за рамки системы. И все твои решения так или иначе будут зависимы и фактически предопределены. А то что стоит во главе то и является добром, а всё противоборствующее по определению злое... если конечно система захочет так сделать) Хотя в идеале конечно такого быть не должно и добро проявляет только добро даже к злу и прежде всего старается его исправить. А зло в свою очередь этому активно сопротивляется, по дефолту всё ненавидит, и старается уничтожить прежде всего... себя) ...почему?) Желание выйти за рамки системы, неудовлетворённость её правилами, также видя возможно её несовершенство и в связи с чем не желанием в ней существовать и т.д. и т.п.
И в идеале если система не совершенна, а соответственно в ней есть ошибки, то она должна рухнуть и аннигилировать. И если зло постоянно ищет безуспешно в ней ошибки и не находит, то естественно злится из-за этого ещё больше, хотя и при этом может постоянно верить и надеяться в то, что когда то найдёт... оох и настанет тогда Рагнарёк)
Вот в примерно таком деструктивном виде должно существовать само зло - постоянно пытающееся самовыпилиться, которому это постоянно мешают сделать добряки, т.к. если ему это удастся, то доказательство окажется засчитанным и всё рухнет, а по пути метёт всё и вся что вокруг, да под руку попадётся в приступах дикой агонии.
...а действительно ли это настоящее зло?)
Думаю про эксперимент с водой и рисом доктора Эмото Масару уже многие знают и знатно на него по плевались в своё время)
Вот он если кому интересно:
В кратце: на 2 из 3 чашек риса с водой говорили разные слова в течении месяца, одной добрые, второй злые, а над третьей просто молчали и игнорировали. Результат - в третьей было хуже всех.
Нуу чтож по этому поводу можно сказать только одно - сказка ложь, да в ней намёк ...)
А дальше всё-таки хочется обратиться к более точной математике и абстрагироваться от всего этого.
Да и вообще откуда было взяться добру и злу? Попробуем для начала представить поле... а ладно это будет сложно) просто массив, пусть будет хоть безразмерный, но заполненный нулями абсолютно весь. Какие вообще операции, внутри массива (системы), (ну или если вне, то с использованием только тех данных о которых знаем, заведомо знакомы, т.е. выстраиваем только с того материала что есть изначально - 0) над таким массивом могут породить там что-то отличное от пустоты, нуля? Сложение, умножение, вычитание, возведение в степень, деление, транспонирование, сортировка ... с некоторыми операциями так вообще сплошная неопределённость возникает.
Так стоп, а откуда мы взяли операции, они у нас из какого ниоткуда вылезли? ...что, что?) аааа что мы наделали? Мы кажется начали копать глубже математики и фундаментальнее! Это ещё что за ужас?!
А фууух, тут кажется ещё не так страшно, оказывается мы не первые такие и в математике уже давно давно существует отдельный раздел называемый - топология.
Раздел математики, изучающий:
* в самом общем виде — явление непрерывности;
* в частности — свойства пространств, которые остаются неизменными при непрерывных деформациях. Например, связность, ориентируемость, компактность.
В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек). Например, с точки зрения топологии кружка и бублик (полноторий) неотличимы.
Который также включает в себя ещё:
* Общую топологию
* Алгебраическую
* Дифференциальную
* Вычислительную
Что также содержат в себе различные операции над уже не просто виртуальными числами (не привязанными к материальной реальности), буковками (переменными, что могут обозначать числа) или массивами, а над тем что уже и является чем-то виртуальным по отношению и к ним и уже и отвязывается от них. Из-за чего многие уже и начинают поговаривать, что топология становится ещё и фундаментальнее математики.
...итак ещё раз, чтоб было точно понятно с чем мы сталкиваемся.
Так например биология - это прикладная химия, химия - это прикладная физика, физика - это прикладная ... <тут ещё N-е количество не открытых наук> ... математика, а математика - это прикладная топология _ нуу или во всяком случае скоро может ей стать)
Ну и поскольку топология оперирует уже больше по сути самими принципами над пространственными или многомерными массивами, то и операции мы уже получаем как что-то само собой разумеющееся, где если например та же гомеоморфность (принцип дырки от бублика :D) присутствует, то она есть и никуда от неё не деться и в любых операциях или изменениях, да даже покое, она будет верна своим принципам.
Т.о. в принципе можно уже потихоньку начинать предполагать, что были некоторые "операции", которые просто напросто сами по себе как данность есть или нет в не зависимости от того явны ли они для чего-либо или нет... эхх и получаем здесь ключевое слово "явны", при котором в теории система может быть идеальной ровно до тех пор пока не объявит о тех или оных)
Но опять же давайте будем отталкиваться от идеала, где у нас они уже по идее для системы все "явны" и открыты, а в результате использование некоторых из оных стало всё что есть во всём многообразии из просто пустоты (правда пока неявным для нас образом) ).
Но куда же тогда стремится зло? Получается что как раз в эту "неявь" небытие... откуда можно запросто явиться? ...видимо) (эххх да вспомнят тут наверно многие ту эпопею с Саргеросом из WoW) НО лишь то что там будет "находиться" (хотя это и по идее не так называется, т.к. там ничего нет, но по другому в этом мире это пока не выразить :) ) - то и будет истинным воплощением зла в его конечном обличии, а всё остальное так просто его прикладное отображение в этом мире)
А что происходит тогда? А вот тогда ему уже всё равно что происходит) оно уже добилось своей цели и ему на всё пофиг) Или если попробовать сказать ещё лучше, то пофиг ему и потому что даже каждое противодействие со стороны какой-либо системы будет обращено в пользу для него прежде всего в рамках этой же системы. И ещё интереснее это звучит в попытках дать понятие антиинформации.
АНТИИНФОРМАЦИЯ. Бесструктурно-тонический (бесструктурно-тоновый, нерациональный) аналог сообщения (сигнала). Конкретная антиинформационная данность - это менее интенсивное иррациональное, являющееся подобием (по тону, а не структуре) более интенсивного, предельного или запредельного иррационального, Антиинформационное всегда содержит в себе момент ожидания и тоновую лестницу потенцирования интенсивности.
--
Что до сих пор мало изучена... хотяяя как впрочем и наряду с информацией)
...такие вот дела)
Найти сумму элементов - дробного ряда
Привет читателем и комментаторам на этом сайте страницы Пикабу. Мой вопрос?!
Каждому математику известен результат для задачи m / 2^m. Задачи по поиску суммы ряда где m или n это натуральные числа от одного до n. (Сумма=2.!)
И вопрос? Если число m будет равно 30 какая получится / С, если посчитать ряд m от 1 до 30 и если возможно посчитать сумму до m равна 255, каким будет решение можно ли её записать в сокращённом виде, И так чему тут будет равна сумма. ? Всем
пока...
Привет всем моя тема задач, интересное решения по теме сложение дробей
Так вот Я хочу узнать, как вы думаете чему будет равно" 1 / 2 + 3/ 4 + 7 /8 + 15 /16, ?, если посчитать это до m / двойка в степени 12. Запишите ответ. На этом, всё всем чау.
Экспонента в жизни- 2. Зачем это нужно?
В прошлом посте мы говорили о том, как пролетели австралийцы с экспонентой.
В этом – постараюсь ответить на главный вопрос жизни Вселенной и все такое.
Где математика экспонента может пригодиться в реальной жизни?
Можно, конечно, скорчить серьезную физиономию и сказать, что,мол:
По экспоненте высыхает земля после дождя, по экспоненте падает давление, когда вы поднимаетесь в горы…. но звучит это как-то по-ботански!
Мало, кто считает диаграммы, придя домой.
Открою страшную тайну:
Вряд ли в жизни придется услышать такое:
- Дайте мне (7! – 6^2+3e^0)^1/4 помидоров и (ln (e^3) ) картофеля, пожалуйста.
- Молодой человек, я не понимаю.
- Мне плевать, я учился не напрасно.
Да, сами по себе занятия математикой неплохо качают мозги (об этом в следующих постах)
Но, если вы не инженер, конструктор, прогер (в некоторых разделах), экономист, аналитик, и прочее ...
То экспонента вам в жизни не понадобится…
Ну, … почти.
Вообще-то, есть одна тема, где понимание экспоненты может помочь. Тема, с которой сталкиваются все.
Она может помочь в мегаважном вопросе –
В деньгах!)
Смотрите:
Положили вы в банк 1000 рублей под 10 процентов годовых.
То есть, за год вклад увеличится в 1,1 раза.
Через год будет 1000*1,1 =1100. Небольшая прибыль за то, чтобы отдать кому-то свои кровные.
А если надолго? Тоже мелочь какая-то, вложить лет на 30 и получить что, 3000 сверху? Да нафига?
Вот здесь останавливается большая часть людей которые задумались над тем чтобы как-то преумножать доходы. Но проблема то в том что считается все по-другому!
Но вот тут-то фишка работает по-другому. Ведь в следующий раз проценты начисляются от нового вклада, от 1100
1000*1,1*1,1 или
1000*1,1^2 =1221 а не 1200. Вообще, кажется, мелочь, но это не так.
1000*1,2^3
И так далее.
За 30 лет вклад увеличится в 17 раз, а за 40 – в 45!
А если вкладывать под 20 процентов то вклад увеличится в 40 раз уже за 20 лет
Вроде разница не очень велика, но чем дольше вкладываете, тем круче рост.
Не какая-то там примитивная линейная функция или тормознутая парабола, график растет Экспоненциально. Даша, напомни, пожалуйста.
Это ярче всего описывает история, как индейцы продали остров Манхеттен буквально за бусы.
Ну,не то что за бисер. за товары общей стоимостью в 60 гульденов (около 24 долларов, на современные – это около 700). Одеяла, котлы, топоры, ножи и ... вампум (индейский бисер, который у них шел вместо денег)
И это приводят в пример того, как белые обманули индейцев. Ибо теперь Манхеттен стоит больше 50 000 000 000 $ . А купили за 30$.
Но, все не так однозначно.
Если бы индейцы положили в банк 30 баксов под 6 процентов годовых, то за 400 лет получили бы почти 400 млрд долларов!
30*1,06^400 = 397 619 212 307
И могли бы скупить весь Манхеттен на корню вместе со всем содержимым.
Есть ощущение, что к этому моменту народ постарше начинает кипеть
Тут есть важный нюанс – все это работает, если экономика и государство находятся в худо-бедно стабильном и рыночном состоянии.
Например, в США частенько были проблемы с финансами и гиперинфляцией. Так в 1865 г., после Гражданской войны, сбережения многих вкладчиков банков резко обесценились и стали мизерными. 150 лет назад.
А у нас, было как
1917
1922...
1924...
1946...
1991...
Ну и по мелочи – 1998, 2014
Но страна-то сменилась. И теперь можно делать стандартные для инвестиций штуки, чтобы минимизировать риски: диверсификация активов, инвестирование в разных валютах и в компании разных стран.
Чтоб, если и профукать все деньги, то только, если вся Земля разом обанкротится.
А вместе оно веселей.
Да,много сложностей- и учиться инвестициям,и опасности- пирамиды, санация банков, падение рынка. Поэтому, кстати и не говорю про проценты более 20 в год- там са-а-а-авсем другие уровни рисков. Но если серьезно сесть и посчитать- 20 процентов в год,если планировать на сколько-нибудь долгий период,очень даже неплохо!
Фонд Уоррена Баффета на протяжении около 50 лет давал среднюю доходность в 20 процентов годовых,. и вот он один из трех самых богатых людей мира, в 2008 и вовсе потеснивший с первого места Билла Гейтса.
Вообще, в европейских странах, не так запуганных этим «Вжух»,
С первой зарплаты народ начинает вкладывать на свадьбу-рождение-обучение детей.
Ну, а что делать, если денег нет? И получить хочется быстрее, чем через 30 лет?
Можно заработать, запустить свое дело.
Но чтобы заработать денег – надо деньги. Стартовый капитал, так его.
Взять его можно у тех, у кого деньги уже есть
Да не так!!! Эй!
Есть более безопасный способ.
Прийти к инвесторам и сказать, дайте денег.
И когда вы пойдете просить денег, вдруг окажется, что права была Марь Петровна, приговаривая
« Учи Сидоров, экспоненту! В жизни пригодится»
Ибо люди, которые дают другим деньги на бизнес, редко когда оказываются совсем уж дебилами.
У дебилов просто не будет много денег. Ну… в теории.
И инвесторов нужно убедить, доказать, что ваш проект – хорошая инвестиция.
И вот тут-то и нужна, оказывается, математика, в том числе, экспонента.
По экспоненте, при хорошей конъюнктуре растут продажи и доход.
Для того, чтобы захватить мир, Макдональдсу оказалось достаточно расти на 15 процентов в год на протяжении 45 лет с 1950 до 1985.
И если бизнес сможет расти по экспоненте хотя бы несколько лет – это уже очень круто.
(то не какая-то абстрактная теория, это вопросы одного из моих взрослых учеников, который запускал новый бизнес. Готовил бизнес-план для представления инвесторам. Математикой занимался "для себя")
Не всегда это работает, но без четкого плана, как и сколько зарабатывать, денег обычно не дают.
Рост акций Эппл. Похоже?
В общем, экспонента – это классная тема)
Следующий пост – про падающую экспоненту и о том, почему мы не пользуемся искусственным золотом (почти).
*Строго говоря, экспонента – это график e^x, где е~ 2,7… (число Эйлера)
Это число и называется экспонентой.,равно как и график. А те что здесь в математике называются показательной функцией. Но в обычной жизни все графики, которые растут пропорционально иксу часто обзывают общем названием экспонентой, а рост графика - экспоненциальным ростом,ибо растет похоже на график e^x. Почему именно 2,7? Об этом как-нибудь в другой раз.
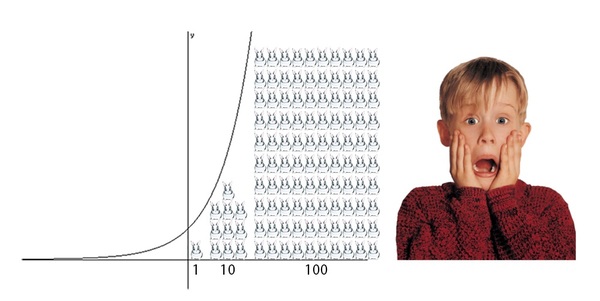
Кролики и экспонента.
Привет! Мы с коллегой -репетиторы по математике.
Так как многие ученики предмета боятся и не видят связи математики и физики с жизнью,будем публиковать здесь статьи связанные со школьной математикой (физикой) в жизни. Может кому пригодится)
Разберемся, как вообще связана с реальностью та жуть, которую проходят в старших классах.
Начнем с показательной функции и экспоненты.
(Это когда начинают с умных фраз: у =2^x, графики чертят, экспоненциальным ростом графиков стращают)
Вот что за хрень, право слово? Ну вот зачем это вообще? Как это вообще связано с реальностью?
Чтобы разобраться, начнем сильно издалека:
Вот это – Великая Китайская Стена
Памятник трудолюбию жителей Поднебесной, защищавший от вторжения варваров. Самое значительное защитное сооружение в истории,видно даже из космоса.
Но мало кто знает о другом защитном сооружении сравнимой длины, которое ограждало от орд вторженцев, и построенном в 20м веке! Совсем недавно, по сравнению с Китайской стеной.
Потоньше, конечно, но по длине похоже.
Знакомьтесь: Великий Австралийский забор.
3500 км!
3500 километров забора, Карл! Ограда длиннее уральских гор
Этот забор ограждает западную Австралию от захватчиков, варваров разрушающих самое ценное, …
Гунны?
Орки?
Гигантские пчелы-убийцы?
Нет!
Все это построено для защиты от одного из главных врагов австралийских фермеров:
Кроликов
Чем эти няшки могли не угодить?
А дело было так:
125 миллионов лет назад, Австралия отделилась от Гондваны, праматерика и стала жить своим умом.
Нужно заметить, ум у нее был… своеобразным.
Выжили такие приколы эволюции как котопес, утконос и ехидна.
В отделении от других континентов власть там захватили сумчатые, так и не догнавшие в развитии более продвинутых – плацентарных.
Ну, жили и жили, как-то существовали. И все было хорошо, пока на континент не приперлись белые люди и не привезли с собой всякую живность.
В 1859 году в своем парке Том Остин выпустил два десятка кроликов, чтобы было на кого поохотиться.
В Европе они мерзли от морозов, их ели лисы и кошки, они умирали от голода зимой.
А в Австралии:
Мягкие зимы, много травы, мало хищников и так себе конкуренты (сумчатые - отстой, по сравнению с плацентарными).
Вау, подумали кролики
И вот тут, наконец, начинается беспощадная математика.
Одна пара кроликов за год может дать 10 пар (или больше) крольчат, которые за это время вырастут и будут готовы к размножению
10
Еще через год 10 пар дадут 10 пар каждая.
10*10=10^2, то есть сотню кроликов, готовых к размножению.
100
Каждая пара из сотни в следующем даст по 10 пар
100*10=10^3=
1000 штук
На исходе 4 года получим 10^4, то есть
10 000
О таких зависимостях и рассказывают умным голосом в 10 классе школы
Показательная функция - для тех процессов которые увеличиваются в разы за каждый промежуток.
10^2, 10^3, 10^4 …
В основнании может быть и двойка, и тройка, и, вообще, любое число, не важно. Такая функция в математике называется показательной – когда меняется Показатель степени, в которую возводим. 10^2, 10^3 и т.д.
А по умному – такой график растет ЭКСПОНЕНЦИАЛЬНО.
Поможет запомнить это умное слово Даша-путешественница.
Экспоненциальный рост – это быстрый рост. Очень быстрый.
Буквально за десятки лет они расселились по всей территории Австралии, увеличили свою численность до миллионов (начав с 24 штук), и стали бедой сельского хозяйства и причиной вымирания некоторых видов.
Не то, чтобы они устраивали терки с местными.
Просто местные не могли больше прокормиться на полях, по которым прошлась орда таких милых внешне пушистиков.
Хм, подумали фермеры, и начали с ними бороться.
Сначала их травили и устраивали охоты.
Потом в 1907 появился тот самый забор, который патрулировали на верблюдах. Увидел кролика – убей, увидел норку – обрушь.
Но все работало хреново.
Капканы убивают ограниченное количество кроликов.
Заборы ограничивают тоже относительно линейно.
А растут то эти заразы экспоненциально. То есть о-о-о-чень быстро. Достаточно запустить за забор пару кроликов и дать несколько лет – и все труды насмарку.
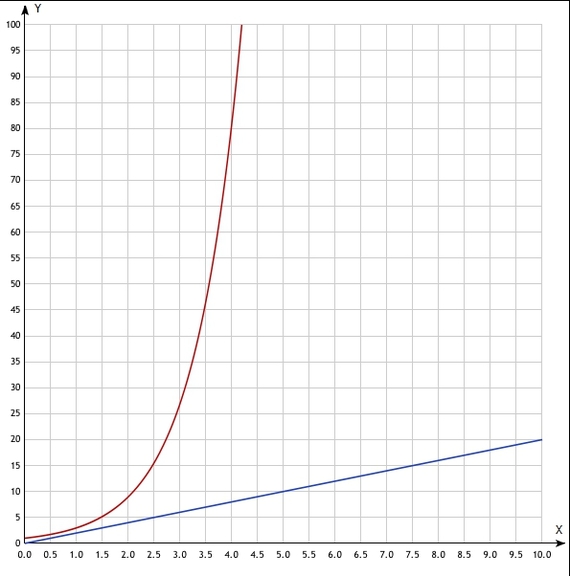
Все было бы понятнее, если б они подумали над математикой процесса.
Смотрим на графике:
Рост численности кроликов – красной линией, а рост отстреленных , попавших в капканы – голубой.
Красная ведет!
И вот тогда начинается весьма жесткая история.
Что может побить кроликов, которые растут вот так, по экспоненте?
Только другая штука, которая так же по экпоненте растет.
Сначала пытались завести хорьков и лис, чтобы они охотились на зайцев. Но те тоже не дураки.
Зачем охотиться на шустрых кроликов, если можно легко жрать квелых сумчатых?)
Так что они только подгадили порушенной экологии Австралии.
Поэтому решили ввезти то, что уничтожает единственно кроликов.
Известная в интернете картинка, заставляющая млеть девчонок.
Кролики, много, мимими!
Но вообще то.
Это не санаторий для кроликов, а концлагерь, где на них испытывают биологическое оружие.
Так как хищники забили на свои обязанности, больше 10 лет на кроликах с картинки на острове Варданг испытывали вирус миксоматоза. Который поражает только кроликов и никого более.
В 1950 вирус выпустили в Австралию – и он стал распространяться экспоненциально. Заражая 1 кролика, который в свою очередь заражал 10 других. И эта экспонента оказалась круче, чем экспонента роста кроликов и буквально за несколько лет количество кроликов с миллиарда уменьшилось до 100-200 миллионов.(что, впрочем, тоже до фига)
Вот так вот, математика с биологией, смогли справится с проблемой, которую создало незнание тех же самых математики с биологией.
Эх,если бы этих ребят учили:
Нельзя, нельзя запускать в эндемичную благоприятную среду новые виды так просто.
Но, история учит нас, что мы ничему у нее не учимся!
Увы, помните ребят, которые патрулировали на верблюдах великий забор? Они защищали от выпущенных в природу двух десятков кроликов.
Когда появились автомобили, они пересели на них. А куда девать оставшееся стадо верблюдов?
"Мы же 100 лет сражались с экспоненциальным ростом травоядных,которых выпустили в природу. Куда девать ненужных теперь верблюдов?"
Правильно! А давайте выпустим их в природу!
Вау, сказали верблюды!
Мягкие зимы, много травы, мало хищников и так себе конкуренты....
Теперь их количество растет экспоненциально и размножившиеся верблюды в поисках воды и травы ломают тот самый забор,который когда то охраняли.
В общем – учите математику!)