Как быстро найти загаданное число
Я загадал случайное число от 1 до 10. Как быстро вы сможете отгадать его? Кому-то повезёт с первой попытки. Кто угодно уж точно отгадает с десятой. В среднем у людей будет получаться за 5 попыток. А как можно точно сделать это быстрее всего? Чтобы это было проще, после неправильного ответа я буду говорить вам, большее или меньшее число я загадал
Правильный ответ — за 4 попытки. Не очень впечатляет: лишь на 1 меньше 50%. Но что если я скажу вам, что я отгадаю 1 число из 100 всего за 7 попыток? И одно из тысячи всего за 10
Знание о том, больше или меньше загаданное число нашей попытки очень сильно облегчает задачу. Например, мы можем предположить число 9. Вероятность попасть в любое число одинакова, поэтому девятка ничем не хуже других. Если она и была ответом, мы победили, а если нет, услышав «меньше» мы будем знать, что и 10 не является загаданным числом! Так можно пройти в 2 раза меньше чисел и мы уже улучшим средний результат
Но есть ещё более эффективный способ. Мы можем взять число из середины последовательности. Если не угадаем, у нас тогда останется ещё половина вариантов, это верно. Но мы избавимся и от целой другой половины! В случае 10 это не так важно, но если нам загадали число от 1 до 100, мы даже неправильным предположением убираем 50 вариантов!
С оставшейся половиной можно проделать то же самое. Давайте посмотрим, как это работает на примере. В начале я загадал число 8. Оно отгадывается всего за 2 шага — это неинтересно. Давайте разберём на примере от 1 до 100. На этот раз я сразу скажу ответ, чтобы вы следили за его поиском: это число 43
–Это число 50?
–Меньше
–Это число 25?
–Больше
–Это число 37?
–Больше
–Это число 43?
–Верно!
Мы управились всего за 4 шага! При случайном угадывании нам потребовалось бы 50. Попробуйте сами так «отгадать» любое число из 1000 — вам скорее всего понадобится даже меньше 10 шагов
4, 7, 10 — почему именно эти числа? Вы могли бы подумать, что я просто прибавляю 3, но это неверно: 1 из 10000 точно отгадывается уже за 14 шагов
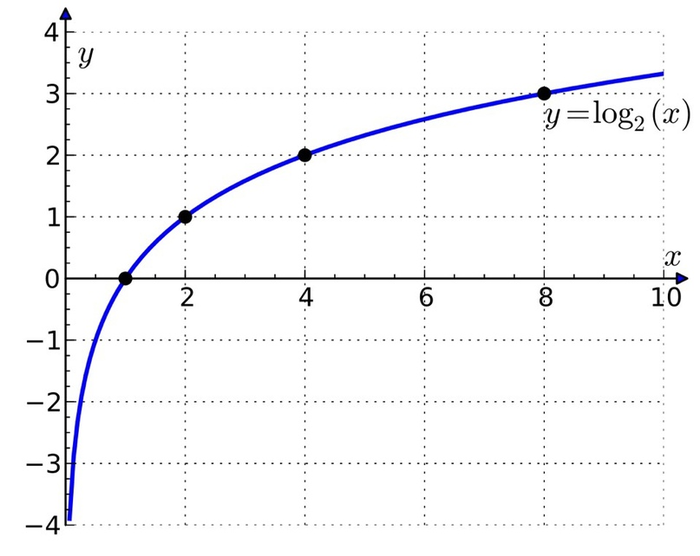
В нашем алгоритме мы каждый раз делим оставшийся интервал на 2. Давайте попробуем решить обратную задачу: через сколько умножений на 2 мы достигнем определённой длины? 2*2*2 = 8 — это всё ещё не равно 10. Но умножив 2 на себя 4 раза — другими словами, возведя 2 в 4 степень, мы получим 16, что явно больше 10. Значит, можно гарантированно угадать число за 4 шага! Математическая операция, которая позволит это посчитать — обратная к возведению в степень: логарифм по основанию 2. Его функция возрастает очень медленно:
Степень двойки растёт очень быстро. С этим связаны известные факты: например, почти невозможно сложить лист бумаги пополам больше 7 раз, что неудивительно — в нём будет уже 128 слоёв! Рвать листы бумаги пополам также с определённого момента становится очень сложно
По легенде древнеиндийский математик создал шахматы и показал их правителю страны. Тому игра настолько понравилась, что он позволил изобретателю самому выбрать себе награду. Математик попросил одно зёрнышко пшеницы за первую клетку, 2 за вторую и так далее до конца доски. Правитель обиделся, что мудрец просит так мало, но повелел выплатить награду. Однако, оказалось, что сделать это невозможно. Количество зерна превышает урожай пшеницы за всю историю человечества, а его масса бы равнялась 1200 миллиардов тонн
Если пронумеровать каждый атом на нашей планете и попросить найти один определённый, это можно сделать всего лишь за 167 раз! У числа атомов на нашей планете, к слову, 50 нулей
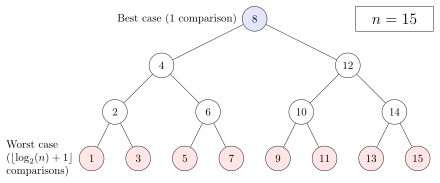
Такой алгоритм поиска широко используется в программировании — там, где количество шагов и время критически важно. Его также можно несколько улучшить. Наша последовательность расположена по возрастанию и в центре находится число 5 (если округлять середину вниз). Но если число загадывает человек, он с большей вероятностью загадает 7. Если расположить его в середине, часто мы будем попадать с первого раза! Также удобно расположив другие числа, можно ещё больше улучшить алгоритм
Если интересны посты про образование и науку, заглядывайте ко мне в группу ВК и телеграм-канал



Лига образования
6.8K постов22.9K подписчика
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)