МатОлимп #9
Добрый день! Сегодня мы с вами разберём задачку, связанную с теорией чисел. Сначала небольшое напоминание: натуральное число n называется составным, если у него кроме 1 и n есть ещё натуральные делители. Иначе число называют простым. Теперь же перейдём к самой задаче.
Пусть p - простое число. Докажите, что 4^p+p^4 является составным числом для всех простых p.
Начнём решение издалека. Все мы знаем выражение для разности квадратов
А есть ли такая формула для суммы квадратов? Есть!
Теперь заметим, что у нас в условии тоже сумма квадратов.
Разложим это выражение по полученной формуле.
Все простые числа, кроме 2 – нечетные. Для двойки проверим наше утверждение отдельно в самом конце. Если же p нечетное, то. p+1 четное и делится на 2. Запишем тогда наше число в виде p+1=2k, где k - натуральное. Заметим, что
Значит, наш корень - натуральное число. Соберём все результаты вместе!
Получается , что наша сумма представима в виде двух множителей. ( заметим, что при p=1 левая скобка обращается в 1 и при p>1 она возрастает). Значит, наше число составное, так как представимо в виде произволения двух натуральных чисел, отличных от 1 и самого себя.
Остался случай p=2. Но тут все просто! 4^2+2^4=32 - составное.
Задача решена!

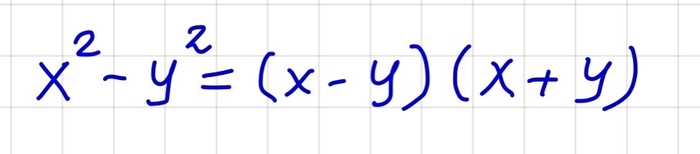
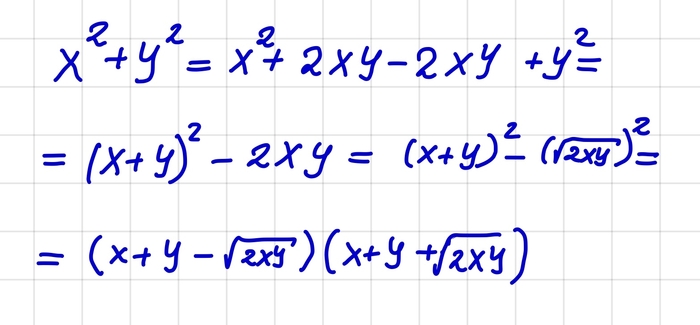
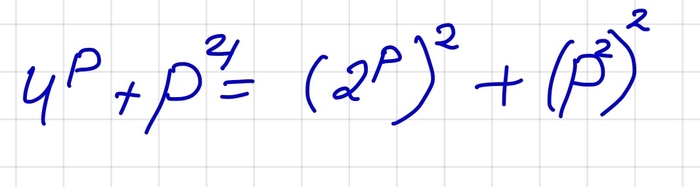
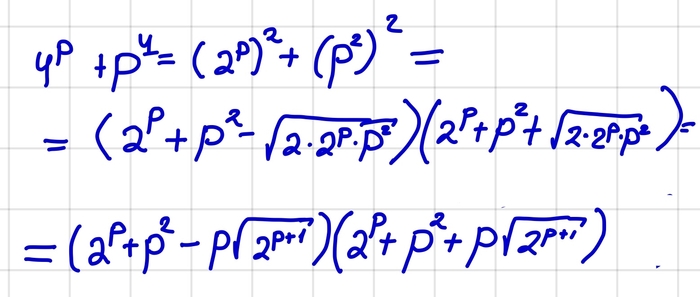
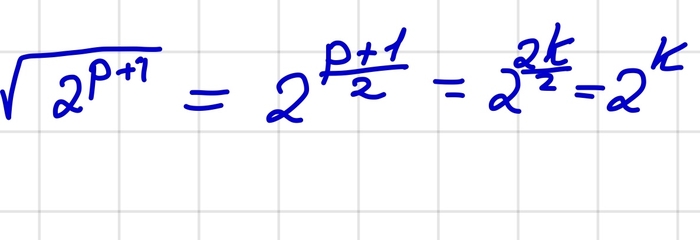
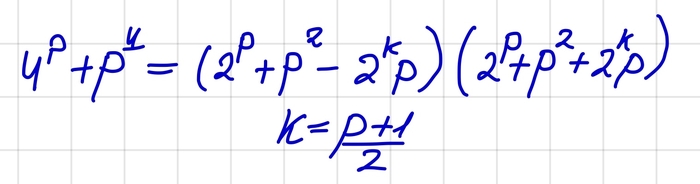
Лига математиков
926 постов2.5K подписчиков