RSA на домашнем Питоне
Доброго времени суток, господа пикабушники! Сегодня мы с вами нарушим все правила шифрования в том числе и правило о "Домашнем шифровании".
Как вы уже поняли, я буду хвастаться перед вами собранным на коленке шифраторе и дешифраторе, написанным на Python.
Итак, преступим!
Начнём с того, что познакомимся с понятием "шифрование".
Шифрование — обратимое преобразование информации в целях сокрытия от неавторизованных лиц. (Честная копипаста с русскоязычного Вики)
Шифрование давно известно людям.
Первым известным применением криптографии принято считать использование специальных иероглифов около 4000 лет назад в Древнем Египте. Криптография египтян использовалась не с целью затруднить чтение, а вероятнее, со стремлением писцов превзойти друг друга в остроумии и изобретательности, а также, с помощью необычности и загадочности, привлечь внимание к своим текстам
Скитала - одно из древнейших известных криптографических устройств
Но вернёмся в современный мир. Для чего сейчас используется криптография? Вы даже не можете представить себе, что она окружает вас везде. Начиная от ваших компьютеров и смартфонов, заканчивая простой ТВ-трансляцией любимого телешоу.
Современные криптографы разделяют 2 основных метода шифрования симметричное и асимметричное.
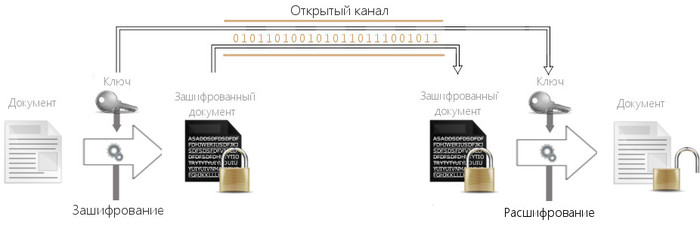
Симметричное шифрование
Способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. Отсюда название — симметричные.
Давайте представим, что я хочу передать вам сообщение с помощью симметричного шифрования.
Возьмём простую фразу:
Шифрование - это здорово!
Теперь переведём её в более простой вид - вид числа.
26-10-22-18-16-3-1-15-10-6 - 31-20-16 9-5-16-18-16-3-16!
(Кстати, такой вид шифрования называется очень просто - "A1Z26" )
Теперь выберем ключ. Пусть им будет число, состоящее из 3 знаков. Будем дублировать его, для получения нужного результата.
Я предлагаю выбрать число 123
Теперь, если мы сложим исходную числовую комбинацию с цифрами ключа вот так:
26-10-22-18-16-3-1-15-10-6-31-20-16-9-5-16-18-16-3-16
++++++++++++++++++++++++++++++++++++++++++
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
Получим результат:
27-12-25-19-18-6-2-18-11-8-34-21-18-12-17-20-19-4-18
Теперь, если попробуем расшифровать такую строку - получим тарабарщину:
щкчсребрйжundefinedуркптсгр
Нетрудно догадаться, что чтобы расшифровать такое сообщение нужно будет применить операции в обратной последовательности.
(Циничная копипаста пикчи с Вики)
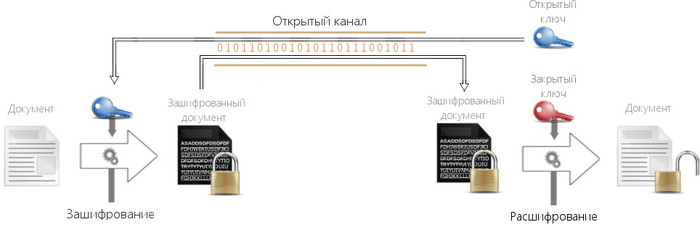
Асимметричное шифрование
Такое шифрование в разы сложнее.
Давайте предположим, что Я - Алиса, а Вы - Боб. Нам нужно безопасно передать друг-другу сообщение. Но к сожалению, Мы вынуждены передавать сообщения друг-другу через болтливую секретаршу, что любит почитать чужие письма. Что делать? Теперь и ключом-то не обменяешься.
Решение лежит на поверхности - нужно передать что-то такое, благодаря чему Алиса мог бы передать Бобу своё сообщение в обход передачи ключа. И тут нам на помощь приходит математика с её простыми числами.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
АХТУНГ. ДАЛЬШЕ БУДЕТ БОЛЬНО. МНОГО МАТЕМАТИКИ.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
Мы воспользуемся алгоритмом RSA. Его создатели Рональд Линн Ривест, Ади Шамир и Леонард Макс Адлеман придумали его и в августе 1977 года в колонке «Математические игры» Мартина Гарднера в журнале Scientific American появилось первое описание криптосистемы RSA.
Читателям также было предложено дешифровать, зашифрованную описанным алгоритмом:
96861477882974310816356989621829961314090575987429823147801394517546222599916951251466223919578122064355124520935708883990555154
За расшифровку была обещана награда в 100 долларов США. По заявлению Ривеста, для факторизации числа потребовалось бы более 40 квадриллионов лет.
Спойлер - фразу смогли разгадать только спустя полгода одновременной работы 16 сотен вычислительных машин. Загаданной фразой оказались слова "брезгливый ягнятник".
Так как же оно работает и почему так сложно разгадать проклятое сообщение?
Дело в том, что асимметричные шифры используют так называемые "Односторонние функции".
Односторонние функции
Односторонняя функция — математическая функция, которая легко вычисляется для любого входного значения, но трудно найти аргумент по заданному значению функции.
Как мы знаем из курса математики 5-6 класса - любое не простое число можно представить в виде произведения простых множителей.
Итак:
10 = 2*5
20 = 2*2*5
А вот из каких простых множителей состоит число 12547864874?
Вот. Исходя из этого мы предполагаем, что факторизация (разложение числа на произведение простых множителей) куда сложнее, чем то же умножение.
Чтобы зашифровать сообщение нам придётся не хило попотеть и найти два НУ ОЧЕНЬ простых и длинных числа :)
Теперь, чтобы вычислить наши ключи и текст нам нужно выполнять такие шаги:
-Выбираются два различных случайных простых числа p и q заданного размера (например, 1024 бита каждое).
-Вычисляется их произведение n=p*q, которое называется модулем.
-Вычисляется значение функции Эйлера от числа Ф(n)=(p-1)*(q-1).
-Выбирается целое число e (1<e<Ф(n)), взаимно простое со значением функции Ф(n).
Число e называется открытой экспонентой (англ. public exponent)
Обычно в качествеe берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые из чисел Ферма: 17, 257 или 65537, так как в этом случае время, необходимое для шифрования с использованием быстрого возведения в степень будет меньше.
Слишком малые значения e, например 3, потенциально могут ослабить безопасность схемы RSA.
-Вычисляется число d, мультипликативно обратное к числу e по модулю.
Число d называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
-Пара {e,n} публикуется в качестве открытого ключа RSA (англ. RSA public key).
-Пара {d,n} играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.
Поздравляю, Вы сломали себе мозг и научились RSA шифрованию. Теперь можете сойти с ума.
Ну а теперь вернёмся к моему говнокоду:
Перво-наперво нам понадобится Python 2.7 и библиотека, для шифрования pycryptodome (Для *nix) и pycryptodomex (Для Windows).
Я строго придерживаюсь мнения, что Pikabu - не Habr и не буду расписывать код принципиально. Ниже в ссылках прикреплены ссылки на GitHub. За говнокод и оформление просьба не кидаться камнями - писал для себя и не планировал писать статьи. Если буду разбирать код на Гитхабе - обязательно отпишу.
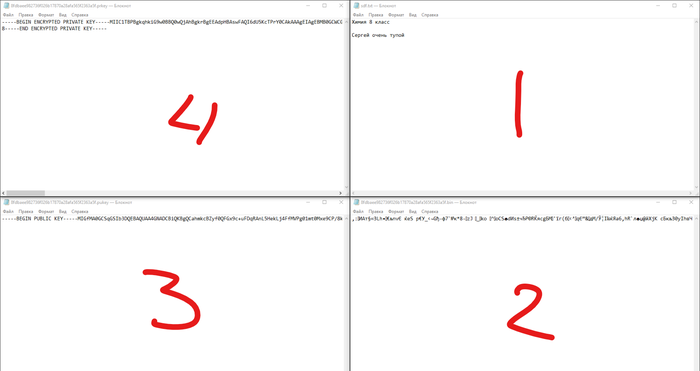
Итак, ниже представлены скрин сухого остатка после работы программы:
1 - исходное сообщение
2 - зашифрованное сообщение
3 - публичный ключ
4 - приватный ключ
Спасибо, что зашли послушать лекцию дилетанта. Всегда рад помочь :3
Мультипликативно-
https://ru.wikipedia.org/wiki/%D0%9C%D1%83%D0%BB%D1%8C%D1%82...
Если у вас возникли вопросы - жду у себя в вк: https://vk.com/barashkoff3
или твиттере: @canusupportme
|
ССЫЛКИ В КОММЕНТАРИЯХ \ /