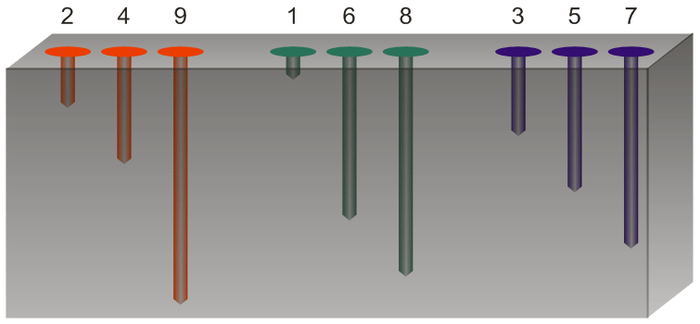
Представьте себе, что я - продвинутый лохотронщик, предлагающий вам сыграть в игру: вы выбираете цвет (допустим, вы выбрали красный) одной из 3 групп по 3 гвоздя каждая, гвозди вставлены в дырки так, что наружу торчат только их шляпки, затем я скрытно от вас перетасовываю вашу (красную) группу гвоздей, а вы, также скрытно от меня, тасуете остальные (синие и зелёные) гвозди. После чего мы делаем одинаковые ставки и тянем жребий: вы вытягиваете гвоздь выбранного вами цвета, а я тяну гвоздь любого другого цвета. У кого длиннее, того и деньги.

Как вариант, позволяющий не допустить подмены во время перетасовок, можно размещать гвозди в 3 вращающихся слотах по 3 дырки каждый и быстро крутить слоты, не отворачиваясь.

Проиграв за десяток-другой ходов некоторую сумму на красных гвоздях, вы подмечаете, что я всегда тянул синий гвоздь и никогда не зелёный. "Ага!" - говорите вы себе. - "Синие гвозди в среднем длиннее". И выбираете синий цвет. И снова постепенно проигрываете, отмечая, что теперь я всегда тяну зелёные гвозди.

Поскольку в том, что красные в среднем короче синих, вы уже убедились в первом туре, вы делаете вывод, что самые длинные гвозди - в зелёном наборе, а мой предыдущий выбор синих был хитрым разводом. Поэтому теперь вы выбираете зелёный цвет, и...

Ответ на вопрос "что будет, если выбрать зелёный цвет?" я предлагаю вам найти самостоятельно либо подсмотреть в исходной статье. Для желающих подумать-посчитать, над гвоздями надписаны их длины в сантиметрах.

Это была математика, а вот вам задачка, "атакующая" один из законов физики, закон сохранения энергии:

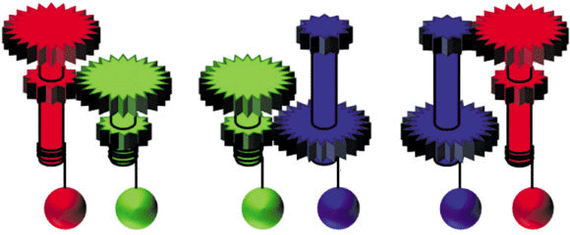
(рисунок автора исходной статьи, но я убрал подсказки, поясняющие, в чём тут дело, хотя и поленился исправлять несогласованность проекций грузиков и шестерёнок)

Как легко заметить, при одинаковом весе грузиков (показаны шариками) в левой части рисунка красный будет, разматываясь с оси красной шестерни, опускаться вниз, поднимая,  в силу разницы передаточных чисел шестерней,  наверх зелёный. Если же отсоединить зелёную шестерню от красной и присоединить к синей (центр рисунка), то зелёный грузик перетянет синий, подняв его вверх. А синий грузик (правая часть рисунка) перетянет красный.

Вечный двигатель? Разумеется, нет. Объяснение, почему нет - опять же, в исходной статье.

Но для понимания предыдущей задачи (про гвозди) важен не "вечный двигатель", а сам факт того, что красный блок "сильнее" зелёного, зелёный "сильнее" синего, а синий "сильнее" красного.  Дочитавшие до этого места уже должны догадаться, что выбрав зелёные гвозди, они также проиграют, поскольку я в этом случае стану тянуть исключительно красные. Которые, казалось бы, "в среднем короче" синих, а те, в свою очередь, "в среднем короче" зелёных. Голландец Оскар ван Девентер даже сконструировал механическую игру, в которой какую бы из трёх шестерёнок вы ни выбрали, оппонент может выбрать после вас одну из двух оставшихся так, чтобы вас победить.

Это парадоксальное свойство специально подобранных групп и правил их сравнения называется нетранзитивностью:

A>B и B>C, но C>A.

Детская игра "камень-ножницы-бумага" отлично его иллюстрирует: камень сильнее ножниц, ножницы сильнее бумаги, бумага сильнее камня (последнее неочевидно и не факт, что верно, но для детишек сойдёт).

А вот игра совершенно на первый взгляд недетская, хотя детишек среди зрителей у неё всегда в достатке. Как, впрочем, и взрослых, включая опытных конструкторов-робототехников. Знакомьтесь: настоящие боевые роботы-гладиаторы в серии игр BattleBots:

Так получилось, что я сам на отдыхе люблю поглазеть на ютюбе, как мочат друг друга и разносят на куски эти механизмы, сконструированные ради одной-единственной цели - уничтожения себе подобных. И я своими глазами наблюдал, что "косильщики" (сверху) как правило быстренько разбирают на запчасти "давильщиков" (снизу и справа), те чаще всего успешно перекусывают "кидал" (слева), а "кидалы" подбрасывают "косильщиков" так, что те трескаются своими рубящими лопастями об пол и стены, несколько раз подпрыгивают и отдают робогу душу.

Как показывает в своей статье Александр Поддьяков, то же самое наблюдается и в живой природе: иначе, существуй некий универсальный принцип "лучшей приспособленности", довольно быстро выявится некий супер-пупер-победитель, который вытеснит всех остальных, после чего ему останется либо подыхать с голоду, либо фотосинтезировать в гордом одиночестве (отравляя воздух кислородом и в конечном итоге также склеивая ласты или что там у него вместо ласт будет). Этого не произошло исключительно благодаря нетранзитивности приспособленности: виды, выигрывающие в чём-то одном, проигрывают в чём-то другом и универсального критерия их сравнения не существует. Более того, виды, выигрывающие против одних по совокупности, сливают по совокупности же другим, которые, опять-таки по совокупности, проигрывают третьим - как раз тем самым, что всегда побеждаются первыми. Ну, на самом деле, там всё гораздо сложнее, конечно, но принцип именно такой.

И даже в хоккее:

И вот теперь мы переходим к тому, ради чего, собственно, автор-психолог свою статью и затеял. К отсутствию единых универсальных критериев сравнения во многих случаях.

Когда некий эксперт сравнивает два предложенных ему решения проблемы, назовём их (1) и (2), он может выбрать из них лучший - допустим, это вариант (2). И абсолютно логично обосновать свой выбор - на то он и эксперт. Но довольно часто бывает так, что другой эксперт, ничуть не менее квалифицированный, сравнит вариант (2) с неким вариантом (3) и столь же убедительно докажет, что (3) лучше, а третий будет сравнивать (3) с уже отброшенным нами вариантом (1) и придёт к выводу, что он-то, (1), и является самым лучшим вариантом.

И это - реальная проблема, какие бы эксперты какой бы выбор ни делали. Выборы президента (во избежание срача не буду уточнять, какой именно страны). Выбор спутницы жизни. Выбор своего пути в этой самой жизни. И так далее.