Как записать число ноль с девяткой в периоде
*Чтение данной статьи может вызвать противоречивые чувства.
**Это о-о-очень длиннопост.
Целью статьи является показать, как можно записать число 0 в виде бесконечной десятичной дроби с периодом 9 стандартными средствами. Сама статья является продолжением поста из Лига математиков с сухим заголовком Формы записи действительных чисел (где в комментариях @nbvehbectw совершенно верно указал суть проблемы: #comment_153360302) и написана под впечатлением от истории из жизни за авторством @Gella4ka: ЯКласс. Сколково. Строить или не строить? (из которой многие с удивлением для себя узнали, что торф является горной породой).
Итак, просто о сложном. Что такое бесконечная десятичная дробь?
Представьте, что вам нужно указать своё местонахождение в пространстве, т.е. фактически указать свой текущий адрес.
Давайте начнём с самого начала:
▪ Вселенная,
▪ сверхскопление Ланиакея,
▪ суперкластер Девы,
▪ местная группа галактик,
▪ галактика Млечный Путь,
▪ рукав Ориона,
▪ Солнечная система,
▪ третья планета от Солнца...
Здесь каждый следующий пункт уточняет предыдущий (т.е. указывает на одну из его частей). Список последовательных уточнений может продолжаться довольно долго.
Так вот: бесконечная десятичная дробь – это адрес действительного числа на числовой прямой, содержащий бесконечный список последовательных уточнений.
Давайте посмотрим, как строится этот адрес и какие нас здесь ожидают сюрпризы. Для определённости выберем число x = 1/2 = 0.5 (в качестве десятичного разделителя будем использовать точку ".").
Во-первых, вся числовая прямая с помощью целых чисел делится на единичные отрезки:
И первое, что мы делаем – определяем, в какой отрезок попадает наше число. Тогда, если прямая – это Вселенная, то, скажем, отрезок [0; 1] – это сверхскопление Ланиакея. При этом уже на этом этапе нас подстерегают сюрпризы. Дело в том, что целые числа (например, 1) находятся на границе двух отрезков и, вообще говоря, могут быть отнесены к любому из них. Конкретно для числа 1 это означает, что его адрес может начинаться и как "Вселенная, сверхскопление Ланиакея" – отрезок [0; 1], и как "Вселенная, сверхскопление Персея-Рыб" – отрезок [1; 2]. Это очень важный момент. Ведь действительно: в точку 1 мы можем попасть и со стороны отрезка [0; 1], и со стороны отрезка [1; 2]. Интересующая нас точка x = 1/2 однозначно попадает в отрезок [0; 1], и первая цифра "адреса" равна 0 (указывает левый конец отрезка).
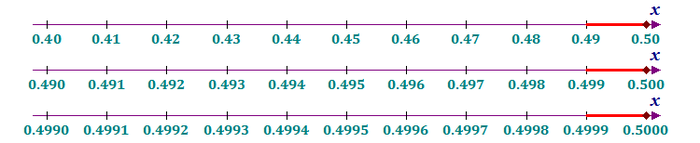
Далее, мы делим наш отрезок [0; 1] на 10 частей (мы ведь строим бесконечную десятичную дробь):
И теперь мы имеем неопределённость: к какому отрезку отнести точку x = 1/2 – к левому [0.4; 0.5] ("суперкластер Девы") или к правому [0.5; 0.6] ("суперкластер Гидры-Центавра"). На самом деле, оба варианта абсолютно равнозначны и нам нет совершенно никакой разницы, какой именно выбор мы сделаем – в любом случае в адресе у нас будет бесконечное количество цифр.
Если мы выберем правый отрезок [0.5; 0.6], то второй цифрой "адреса" будет 5, а следующей (и всеми остальными за ней) – 0:
Таким образом, правый "адрес" числа x = 1/2 будет x = 0.5000... = 0.5(0).
Следует отметить, что все нули здесь важны, т.к. каждый из них указывает на положение числа x = 1/2 в следующем "подадресе": континент, страна, область, город, улица, дом, корпус, подъезд, этаж, квартира, комната, кровать, подушка, и т.д. – список уточнений можно продолжать (в случае действительного числа – до бесконечности). Короткая запись в виде конечной десятичной дроби x = 0.5 имеет тот недостаток, что она ничего нам не говорит о том, абсолютно ли мы уверены, что все последующие цифры равны нулю. Например, измерение в 49.5 см может на практике означать и 49.51, и 49.53 (и даже 49.49) – всё зависит от точности измерительного прибора. При этом запись x = 49.5(0) говорит нам о том, что да – это честные 49.5 см.
Теперь рассмотрим левый отрезок [0.4; 0.5]. В этом случае второй цифрой "адреса" будет 4, а следующей (и всеми остальными за ней) – 9:
Таким образом, левый "адрес" числа x = 1/2 будет x = 0.4999... = 0.4(9).
По "точности" указания положения точки x = 1/2 оба "адреса" совершенно равноправны (хотя это и не совсем очевидно из приведённых рисунков), т.к. суть такого метода адресации заключается в следующем: вы заранее не знаете, где именно находится точка x, а просто на каждом шаге уверены, что она находится в пределах того отрезка, который написан на конверте (а уточнить положение сможете на следующем шаге, и т.д. до бесконечности). В общем случае, обойтись меньшим, чем счётная бесконечность, количеством цифр, к сожалению, невозможно.
Из данной истории мы можем сделать вывод: если на каком-то этапе наша точка попадает точно на границу двух отрезков, то она всегда будет иметь два адреса (построенных по приведённой схеме). Вообще говоря, такая ситуация происходит всегда, когда что угодно оказывается на границе. Например, сверху стакан кажется наполовину пустым, а снизу – наполовину полным. Полночь – это конец предыдущих или начало новых суток? 60-я секунда заканчивает предыдущую минуту или начинает новую? Кстати, бывают такие минуты, которые состоят из 61 секунды (и с каждым годом их становится всё больше). Про календарь от Рождества Христова (и пропущенный нулевой год) я здесь даже не буду начинать разговор. И про резкое падение рождаемости в России в феврале 1918 года тоже не скажу ни слова.
Если вам нужна ещё аналогия, то, например, последний день предыдущего месяца (скажем, 31 декабря) вы смело можете считать нулевым днём следующего месяца (0 января). Это очень удобно, т.к. запомнив, на какой день недели выпадает нулевое число текущего месяца, вы точно будете знать, что на этот же день недели выпадает также 7-е, 14-е, 21-е и 28-е число. А про то, в каком году началось новое тысячелетие (в 2000 или в 2001), я, пожалуй, тоже разговор заводить не буду.
Итак, мы выяснили, что все конечные десятичные дроби могут быть записаны в виде бесконечных десятичных дробей двумя способами. Надеюсь, с этим все согласны. Но как же это поможет нам записать число 0 в виде дроби с периодом 9? Обратимся к нашей схеме: число 0 расположено на границе двух отрезков: [–1; 0] и [0; 1]. Если мы выберем второй вариант, мы получим стандартную запись 0 = 0.(0). Если же мы выберем первый вариант, то целая часть у нас получится отрицательной (–1), а дробная – положительной (0.999999...). В школе сегодня не учат записывать такие числа. Но обратимся к истории.
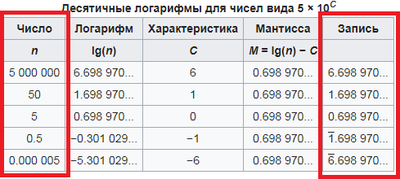
Ключевое слово здесь – десятичный логарифм (думаю, на этом этапе многие уже догадались, к чему я веду). Как известно, любое положительное действительное число можно записать в стандартном виде в виде произведения некоторого множителя, большего 0 и меньшего 10, и некоторой степени числа 10.
Например:
149 600 000 км = 1.496×10⁸ км – расстояние от Земли до Солнца,
31 536 000 с = 3.1536×10⁷ с – число секунд в невисокосном году,
384 400 км = 3.844×10⁵ км – расстояние от Земли до Луны,0.495 м = 4.95×10⁻¹ м – характеристический размер.
При логарифмировании по основанию 10 результат распадается на две части: логарифм степени десятки даёт целую часть (характеристику), а логарифм множителя – дробную часть (мантиссу). При этом характеристика всегда получается целой (но может быть отрицательной), а мантисса всегда заключена между нулём и единицей:
lg(3.844×10⁵) = lg(10⁵) + lg(3.844) = 5 + 0.585 = 5.585,
lg(4.95×10⁻¹) = lg(10⁻¹) + lg(4.95) = –1 + 0.695.
В последнем случае (когда характеристика отрицательна) для удобства придумали специальную запись со знаком минус над целой частью:
–1 + 0.695 = ̅1.695.
Многие школьники прошлого века (в том числе некоторые современные дедушки и прабабушки) были хорошо знакомы с такой записью. Её можно встретить в "Основах математического анализа" Фихтенгольца и школьных учебниках под редакцией Колмогорова. Встречается она и в Википедии:
https://ru.wikipedia.org/wiki/Десятичный_логарифм
https://en.wikipedia.org/wiki/Common_logarithm
Таким образом, чтобы записать левый "адрес" числа 0, мы можем воспользоваться указанным приёмом:
–1 + 0.999999... = ̅1.999999... = ̅1.(9).
Такая запись выглядит вполне логичной:
если 1 = 1.(0) = 0.(9),
то 0 = 0.(0) = ̅1.(9).
На этом пока всё. Но если вы хотите спросить, является ли 0 натуральным числом, может ли в военное время значение π достигать 4, а синуса – 5, то ответ на все эти вопросы: "Да, если вам так угодно (и вы хорошо понимаете, что именно вы хотите спросить)". Но это уже совсем другая история.













Наука | Научпоп
9.4K постов82.8K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.