Захотел поиграть в паровозики. Железнодорожный tileset на шестиугольниках
Присказка.
Итак. По просьбе телезрителей (вы же удаленно глазками на мониторе это будете читать, верно? Значит зрители. =) ) выношу простыню своего имха на общее обозрение в форме поста, або формат комментария явно узок.
Так-же прошу заранее меня простить, я буду много и долго разливаться мысью по дереву, уходя повествованием во все стороны. Ведь текст все-таки сущность одномерная и дискретная, он весьма плохо подходит для описания цветного и многомерного мира. Воспринимать текст надо некоторым образом "сразу и одновременно".
Букаф будет много, напоминать мне что кг\ам не надо, я это и без вас давным-давно знаю, яд употребляю регулярно. Обещал позвать epicrocus, вот зову - @epicrocus. Но наверное (наверное) это открытие «на шестиугольниках» чисто для меня открытие и вам возможно будет скучно. Но раз обещал – то вот.
И еще что скажу: в общем-то желания распространяться об этой идее ввиду ее сырости изначально не было, но я понял что до реализации моими руками дойдет черт знает когда, поэтому держать ее при себе нет смысла. Пусть будет, может кому-нибудь понравится. Может найдутся 3д-печатники которые попробуют именем копи-лефта реализовать что-то подобное, а может даже и… впрочем посмотрим.
Начало.
Начать, наверное, надо с того как вообще эта мысль мне пришла в голову. А все просто - у меня родился сын. А это значит, что теперь я на совершенно легальных основаниях наконец-то могу ходить в игрушечные магазины и снова хотеть железную дорогу. Нука признайтесь, кто из нас не хочет железную дорогу? =) Пошел я значит искать железные дороги, читать за масштабы моделек и прочее, и нашел. И удивился, говоря цензурно, ценам. И тут приходит мысль, а что мешает мне ее сделать? Да в целом ничего, мало того, уже даже были попытки. В детстве отец учил меня делать из картона всякие крутые игрушки себе самому. Я ими даже приторговывал в школе. И тогда еще мы еще с одноклассником делали попытки создавать игрушечные путЯ, но к сожалению доступный нам серый картон "ладога" был капец убог в целом, и в частности в части износа будучи в качестве путей. А до этапа как сделать руками картон нужных характеристик из газеты мы тогда еще не доросли. Плюс я еще тогда будучи второклассником понял, что мероприятие весьма серьезное, трудоемкое, поэтому для разделения нашего труда надо какое-никакое но проектирование. Одноклассник-же Макс так увлекся, что собрал модель вантового моста длиной пролета больше метра - реально вместе с подъемами он по длине был как весь его стол.
И вот почти тридцать лет спустя я снова подошел к этой задачке. Но теперь-то у меня есть 3д принтер, интернеты, вы, и целая куча всего! Пора озадачится что делать и как.
Ближе к теме.
Так как ждпутя вещь в пространстве двумерная, и повторяется в оном пространстве с некоторым постоянством на длину звена... а я тот еще геймер со стажем во всякие стратегии, и я видел зенит популярности симсити, транспорт-тайкун-делюкса и уважаю факторию, то я естественно пошел смотреть как уже организованы железные дороги в компутерных играх. А организованы они на плитках, они-же "тайлы" (на айтишном суржике). И я нахожу статью на пикабу, где товарищ @JamaicaMURR уже плотно подумал над этим (давай выходи из бани и присоединяйся в каменты):
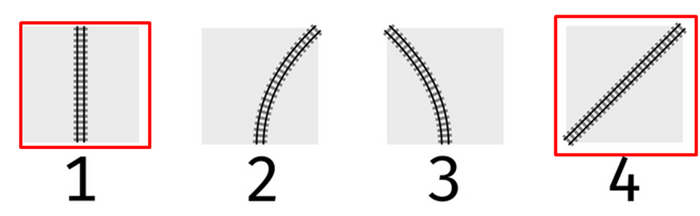
НО! Затея-то была сделать игрушечные жд пути. Реальную такую игрушку, которую можно пощупать руками. А значит наличие двух прямых сегментов разной длины (по короткой, и по диагонали, см. картинку) как у него, совсем не подходит. Я, работая техподдержкой не первый год, ответственно заявляю: если дать возможность собрать "как-то не так", то пользователь именно криво и соберёт. Исключить-же диагонали (делать без четвертого варианта) на квадратных плитках принудительно и полностью ну совсем как-то не комильфо, какие-то одни сплошные повороты получаются, а оставить их – в реальности поедет вся сетка и собрать ее обратно никакой возможности. У единички длина 1, у четверки - корень из двух. Не выровнять потом никак по всей видимости.
Проблемный элемент, если его делать в реале.
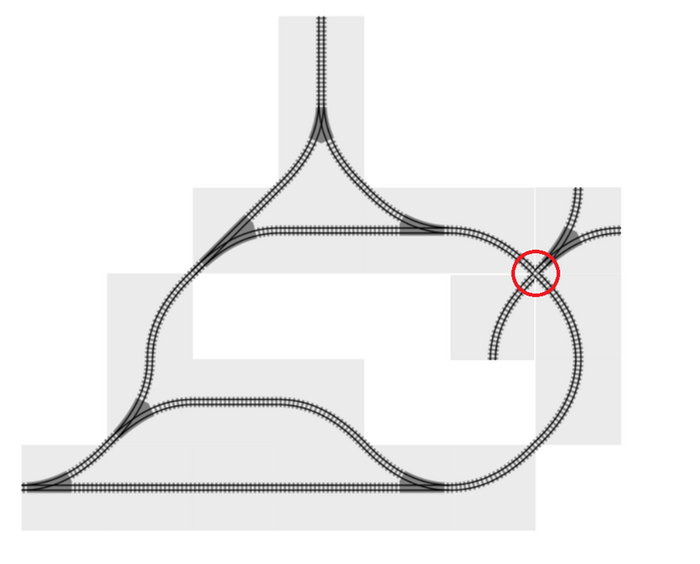
Надо что-то думать. Первое естественное требование: тайлы надо такие, чтоб их можно было вращать, то есть они на плоскости и они правильные. Потом выкристализовывается второе не явное требование – прямые в тайлах должны быть все одной длины. Дальше, медитируя на картинки из статьи уважаемого JamaicaMURR, стало понятно, что пользователь легко из его набора сделает пересечение из данных ему в руки кусочков. Легко! На углах. А стоящего над игроком компьютера, который не дает этого делать, в моем случае просто нет.
Играющий может впелить перекрестие из существующих элементов.
Отступление: @JamaicaMURR, это не критика «в пух и прах» твоей статьи, твои измышлизмы используются в качестве почвы! За что тебе большая благодарность.
Так родилось третье требование - невозможность сделать из набора плиток никаким способом (кроме явного) пересечение путей. Но в чем блин проблема-то? А как обычно - соседи. Рассматриваем соседей. Все дело в соседях. И в тайлах. Тайлы… соседи… плоскость… Но что мы делаем с плитками, на которых у нас находятся разного рода прямые рельсы, стрелки, повороты? Замощаем плитками плоскость говоря математически. За-мо-ща-ем. ХМ! Да про это-же целых несколько лекций вещал Алексей Владимирович Савватеев, вот например: https://www.youtube.com/watch?v=5CQxcFHJIJA которого я почему-то, когда-то, чисто из любопытства смотрел. (Очень рекомендую. Оказывается мы, как человечество, не уверены что знаем даже о выпуклых пятиугольниках, хотя казалось-бы. А ведь считаем себя дофига пупами, хех). И какие варианты есть?
Собственно Что меня удивило.
А может попробовать шестиугольные плитки? Да, они в играх не столь популярны в отличие от квадратов, несколько сложны в реализации, но может что-то получится? И я начал отрисовывать варианты, опираясь на комбинаторику JamaicaMURR, и вглядываться в правильные шестиугольники.
И в них, шестиугольниках, полезли разные интересности:
1. естественно кусочек можно выдернуть из мозаики, повернуть и вставить обратно на место, как и квадрат. Он-же правильный. (треугольники я вообще не рассматривал, ибо в моем случае пути нарисованные на них были-бы одним сплошным поворотом). Прямая соединяющая середины сторон всегда одной длины.
2. у шестиугольника все соседи доступны через сторону. Не через точку. Переходя через точку на шестиугольниках ты попадаешь в торец стены соседей. Т.е. других прямых кусков не надо в отличие от квадратов, где диагональные соседи доступны через общую точку. (И тем более в отличие от треугольников. Там дак вообще целый букет соседей через каждую точку). А других правильных многоугольников, таких чтоб без пробелов заполняли собой плоскость в известном нам 2d нет.
3. у шестиугольника наименьшее количество соседей из всех плоских фигур. Всего шесть.
То есть вот что поразило, что эти свойства выполняются одновременно: правильный шестиугольник можно вращать с шагом 60, все соседи у них через сторону, соседей меньше всего.
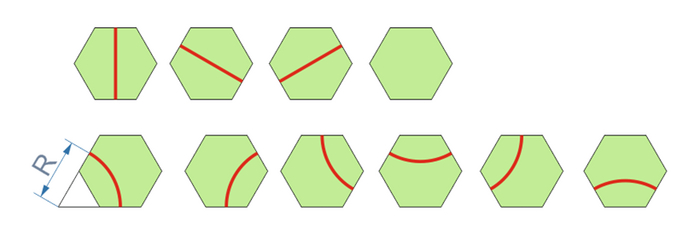
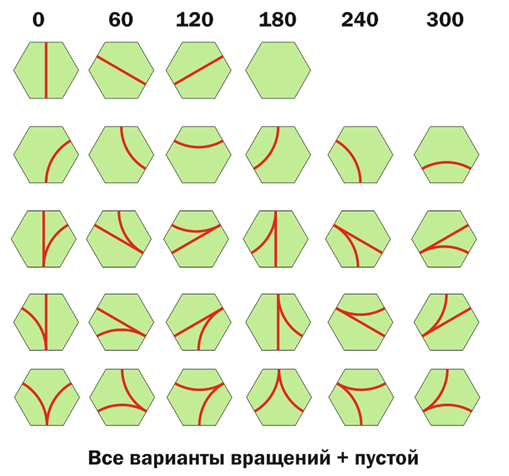
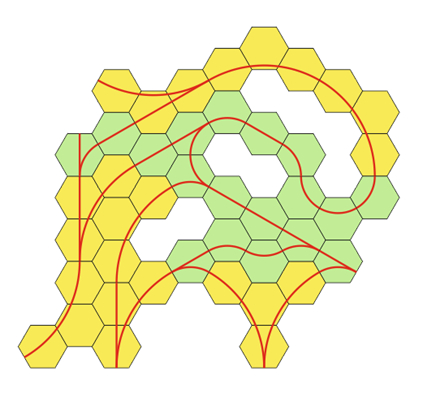
Ну хорошо, а какие могут быть варианты путей на этих плитках? Нужно ехать прямо и все прямые куски одинаковые? Сделано. Нужно поворачивать и тоже одинаковыми кусочками? Окей. Плюс поворачивать составом желательно как и на взрослой дороге – с максимальным радиусом. Т.е при создании поворота соединяем нижнюю сторону и какую-нибудь из несоседних, вот так. (С минимальным радиусом «к соседней стороне» поворачивать я не буду т.к. слишком мал радиус.) И оказывается на шестиугольнике такой центр поворота лежит аж вне габаритов плитки. Шикарно! И плитка «поворот» так-же остается одна: поворот либо налево либо направо, достигается просто поворотом кусочка.
центр поворота далеко.
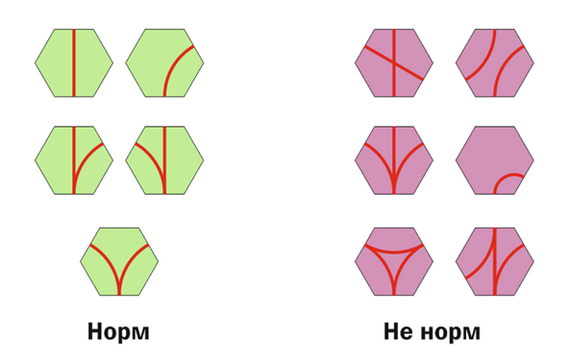
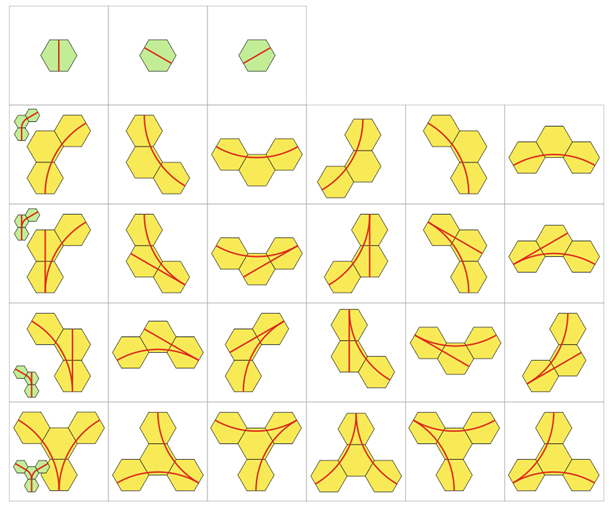
Дальше комбинаторика вариантов "парочками" с прямой и поворотом как товарищ в статье. Всего получается… пять уникальных вариантов. И всякие запрещенные – с двумя непересекающимися поворотами на одном тайле. Такой не пойдет скорее всего из-за габаритов паравозика, так что его… да просто не буду делать, как и товарищ выше на квадратных тайлах и все. Перекресток двух прямых туда-же, его просто не будет во избежание аварий. Есть еще вариант тройной стрелки на одном тайле, но на взрослых дорогах его стараются избегать, так что и я его тоже откидываю. И не стоит делать две стрелки на одном тайле чтоб не путаться с адресацией. И три стрелки тоже не будем. Один таил=одна стрелка.
И вот в чем тут фокус именно "на шестиугольниках" – если не давать вариантов путей игроку, то он и не сможет создать проблем из уже имеющихся у него в руках! Все соседи доступны только через сторону!
Красненькие не создавать чтоб не было проблем.
Собственно и вот! Эти великолепные свойства правильных шестиугольников сводят всю идею к пяти основным звеньям железнодорожной игрушки если она на плоскости. И вот как получается. Не отказал себе в удовольствии пораскладывать всякие варианты. Набросал библиотеку плиток.
Вращайте плитки господа
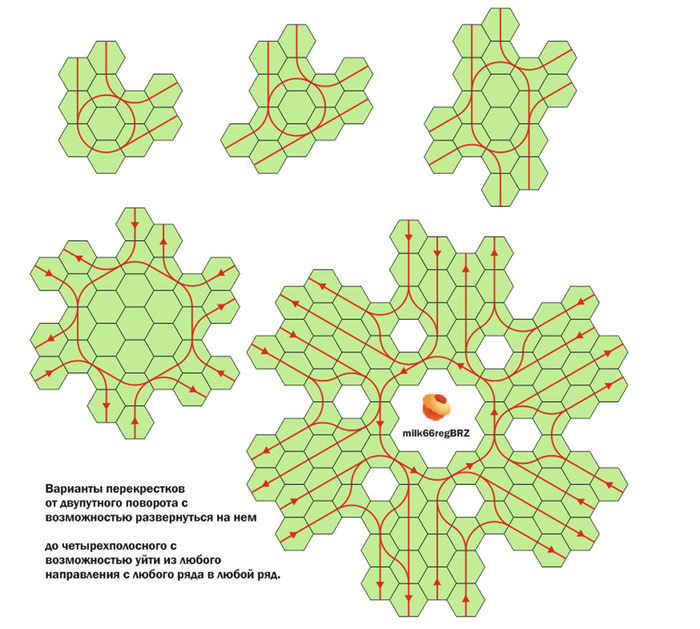
И пораскладывал. Например двупутный перекресток с возможностью развернутся на нем. И даже четырех путный (по две полосы в каждую сторону). И можно продолжать расширять.
Всякие перекресточки
И в общем-то на этом месте пора запускать слайсер, принтер, сидеть моделить и пытаться различного рода варианты практической реализации: от действительно дороги с двумя рельсами и с прибамбасами, до просто пропиленного паза в дощечке по которому скользит два направляющих мотор-телегу пенька.
Радиусы
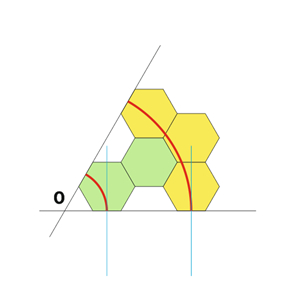
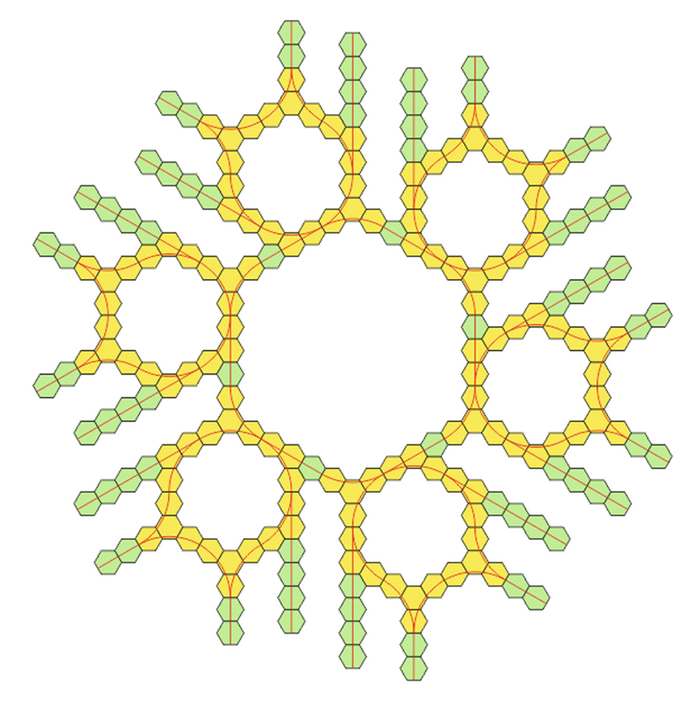
Но сначала оступлю про радиусы. Точно так-же как и «на квадратах» на шестиугольниках тоже можно дополнительно увеличить радиус поворота занимая им по три смежных клетки. Например для пущей скорости. Весь этот набор, назовем его «желтый», остается полностью совместим с «зеленым» набором т.к. наклон касательных и центр совпадают при совмещении (голубые линии на рисунке).
Касательные касаются и наклоняются одинаково на обоих вариантах.
Топологически да, их можно заменить и первым (зеленым) вариантом. С учетом всех поворотов получается вот такой набор. Прямые остаются те же.
Набор "скоростных" поворотов и стрелок.
Желтые элементы вписываются в общую сетку и не нарушают ее (с чего бы им это делать).
При миксовании радиусов они не ломают сетку.
И изза совместимости топологии можно взять и заменить, допустим в перекрестке, все зеленые повороты и стрелки на все желтые раскукожив всё вширь. Красиво получается:
Но тут у меня происходит «жизнь» (как у Конвея, хех. Кстати! @epicrocus попробуй поискать за клеточные автоматы и игру "жизнь", хоть она и не совсем игра, но очень красив процесс. Как простое правило порождает такие зубодробительные структуры.) Я перекатываюсь на время ремонта из своей квартиры к родителям, живу на чемоданах, но мысль не остановить, и мысль виляет маленько в сторону, очень хочется погонять паровозики, а печатать нет ни времени ни средств ни места. А почему-бы действительно и не сделать какую-нибудь виртуальную шпунялку-каталку паравозиков по путям.. то есть…
Игру?
Конец первой части.