Столото. Учимся считать и немного программировать.
Вчера @uncleHarry написал увлекательный пост c попытками математически обосновать, что лотерии Столото — жульничество. Пост вылез в горячее и получил больше 1800 плюсов. Возможно, Столото и в самом деле жулики (поводов так думать предостаточно, хотя бы не прямой "прямой эфир"), но доказать, что там что-то не так с точки зрения математики, нашему товарищу на самом деле не удалось.
Для желающих повторить расчеты: список результатов тиражей лотереи "5 из 36" с номерами от 7269 до 7802. В файле в первом столбце номер тиража, затем 5 выпавших шаров и ещё 1 дополнительный, если я правильно понимаю, он влияет на выигрыш суперприза. Рассматриваются только 5 "основных" шаров.
@uncleHarry предложил два "противоречия" с теорией вероятности.
1. Частота выпадения троек последовательных чисел (без разницы, подряд ли и в каком порядке). Если записывать числа "по кругу" (чтобы после 35, 36 шли 1, 2 и т.д.), по его расчётам тройки соседних чисел выпали в 22 случаях из 459, хотя должны выпадать примерно раз в 99 тиражей — в 4,7 раз реже.
Проверяем: из 534 розыгрышей тройки выпали 26 раз, частота выпадения примерно один раз на 20,5 тиражей.
В теории: запишем числа по кругу и выпишем подряд 5 расстояний между соседними числами (например, если выпали числа 2, 3, 5, 8 и 12, то выпишем 1, 2, 3, 4, 26). Нетрудно сообразить, что сумма выписанных разностей равна 36. Если выпала тройка последовательных чисел, то среди разностей есть две соседние, равные одному.
Посчитать, сколько всего возможных разложений и сколько из них подходят, можно с использованием компьютера (использованная программа). Получается, из 52 360 возможных разложений тройка появлялась 2 480 раз — примерно 1 раз на 21 тираж (неплохое совпадение с реальностью).
2. В исходном посте утверждалось, что если числа выбирались бы действительно случайно, то расстояния между числами были бы примерно одинаковы, и чаще всего встречалось бы 7 (@uncleHarry говорил немного не этими словами, но об этом). Однако в действительности часто было расстояние 1 (275 пар на 459 розыгрышей), чего якобы быть не должно.
Это, разумеется, неправда. Можно провести аналогию: 5 жадных алкашей делят 36 бутылей водки (отливать из бутылей ничего нельзя). Какова вероятность, что всем достанется почти поровну? Даже без всяких подсчётов ясно, равенства в большинстве случаев не будет, практически всегда будут более наглые, которым достанется много, и менее наглые, которым не достанется почти ничего.
Подсчет показывает, что из 52 360 разложений 29 920 разностей будут равны одному, или среднее время появление пары соседних чисел равно 1,75 тиража. В реальности появилось 311 пар на 534 тиража, или 1,72 тиража на пару. Опять-таки, отлично согласуется с теорией.
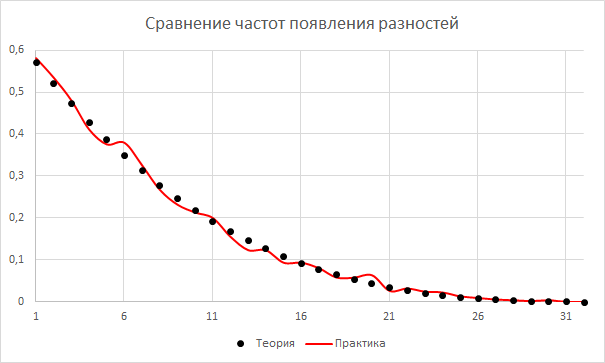
Чтобы уж была хоть какая-то картинка, сравнение частот появления разностей: предсказанное расчетом и то, что получилось в действительности.
Мораль: если организаторы и жулики, то таким образом их не поймать.