Упоротые расчёты - олимпиадная задача
Вот такую задачку я нашёл на просторах интернета. Привожу ссылку на видеоролик:
Мне стало интересно ни сколько решение (хотя, вопреки названию канала, выпустившего ролик, это изучают в школе), столько само выражение. Давайте над ним поиздеваемся.
Может ли р быть математической функцией от х? По идее может, ведь математическая функция - это такая вещь, где множеству одних чисел (у нас это х) приводится в полное соответствие множество других чисел (у нас - р(х) ). То есть для каждого х есть соответствующее р, заданное математически. Мы даже можем аналитически задать эту функцию, переместив её значение в одну область, а аргументы - в другую (хотя итак норм смотрелось, тут я минус пропустил, не серчайте, он вроде для нас не важен):
У этой функции есть производная, и она тоже представляет собой изменяющуюся математическую функцию - это будет важно. Вернёмся к изначальному выражению:
Мне вдруг захотелось его (вот прямо так) продифференцировать:
Продолжаем издевательство, давайте найдём экстремумы функции, при таких х производная обращается в 0. Если вместо р' мы подставим нули, тогда получается (х0 показывает, что это уже конкретное число, а не множество)
При каких х0 данное выражение имеет смысл? Правильно, при любых (это линейная функция, которая определена на всей числовой прямой). Из этого следует, что производная нашей функции всегда должна быть равна нулю, а из этого следует, что наша функция р может быть только числом, только тогда может быть получена производная, которая всегда ноль:
И вот как так? Где я вас обманул? Как получается, что мы получили столь разные результаты?)
ЗЫ: Данный пост написан, чтобы немного поломать голову. Люди с особой чувствительностью, которые заявят об этом в комментариях, будут помещены в особых список чувствительных людей после моего ответного сообщения "Ваше мнение итить-колотить как важно для меня"


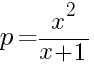
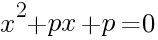
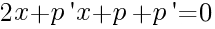
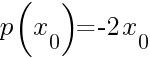
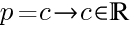
Лига упоротых расчетов
497 постов7K подписчиков
Правила сообщества
Лига занимается странными веселыми подсчетами на основании уже имеющихся в общем информационном доступе знаний. Расчеты - ради лулзов и хорошего настроения. Не нудите сами и не занудничайте в адрес других, играть в Шелдона Купера хорошо до определенного предела.