Парадокс треугольника бесконечности
Заранее извиняюсь за простоватые и местами кривые картинки и графики. Хотел сделать красиво, но пока искал редакторы и пытался их освоить, шли годы, так что решил, или выложу как есть или неизвестно когда.
Для лл, кому лень читать, видео выложил на моём ютуб канале:
Итак начнём. Данный парадокс, я обнаружил, ещё учась в школе, делая уроки по геометрии. Всюду, где бы ни сталкивался с чем-то необъяснимым, я пытался следовать логике. Как известно, геометрия - одна из математических наук, которая больше других опирается на логику.
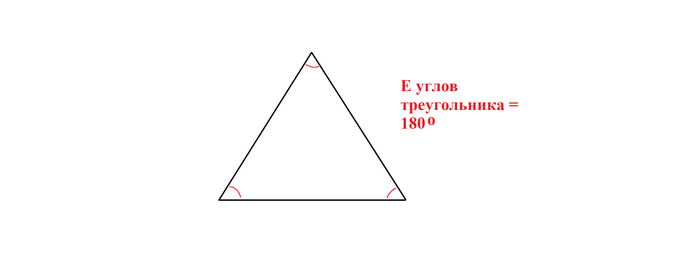
Для начала вспомним, чему равна сумма углов треугольника на двумерной линейной плоскости? Правильно, 180 градусам.
Рис. 1. Сумма углов треугольника
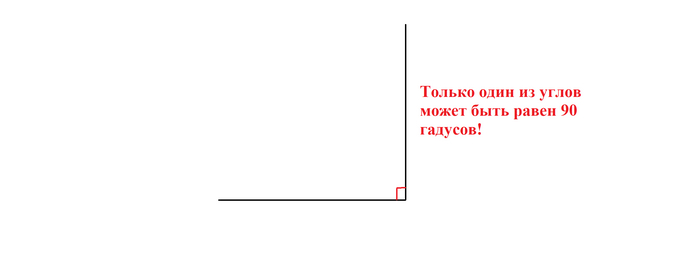
Также есть ещё одно правило, которое гласит, что только один из углов может быть тупым или прямым.
Рис. 2. Правило прямого угла
Нужно ли пояснять, что если хотя бы два угла будут прямыми или более, то стороны треугольника не соединятся и третьего угла попросту не будет.
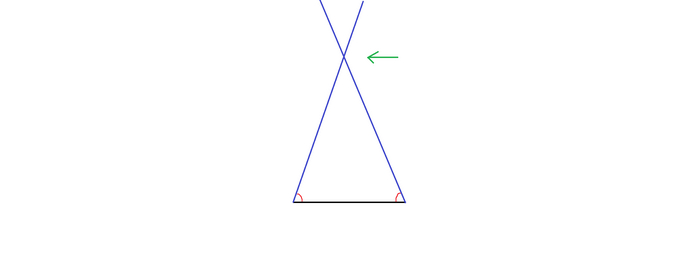
А теперь представим, что у нас есть основание треугольника и по краям данного основания мы разместили по мощному лазеру, направленными к вершине третьего верхнего угла и которые мгновенно пронзают ткань пространства и уходят в бесконечность (рис. 3).
Рис. 3. Пересечение лазеров
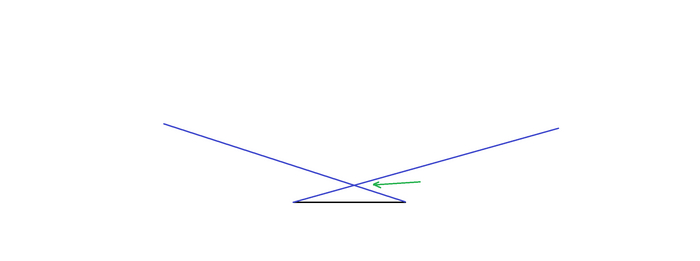
Там, где эти лазеры пересекаются, образуется верхняя точка треугольника и его верхний угол. Отбросим физику и сделаем допущение, что лазеры мгновенно создали по бесконечной прямой. Сейчас углы, образованные основанием треугольника и лазерами, острые. А теперь, начнём постепенно разводить эти лазеры в стороны, постепенно увеличивая углы у основания (рис. 4).
Рис. 4. Сдвиг лазеров
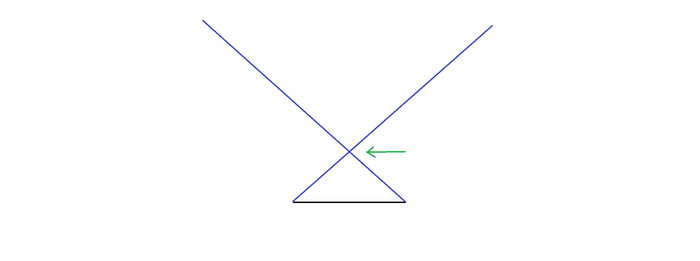
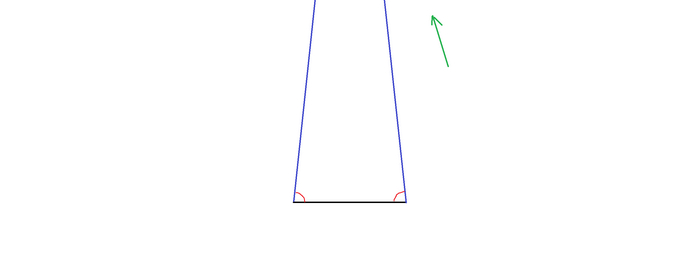
Как видно, точка пересечения этих лазеров сдвинулась выше. Давайте ещё раздвинем эти лазеры. Обратите внимание, что углы у основания тоже увеличились. (рис. 5).
Рис. 5. Сдвиг лазеров продолжается
Раздвинем их ещё немного. Точка пересечения ушла ещё выше (рис. 6). Сейчас она прошла путь, примерно за пару галактик. Если бы мы раздвигали лазеры с постоянной скоростью, то данная точка имела бы постоянное ускорение в астрономической прогрессии.
Рис. 6. Точка ушла за горизонт, углы почти прямые
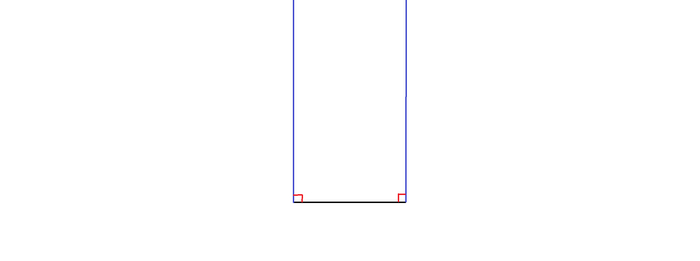
Продолжим ещё немного раздвигать лазерные лучи... А я напоминаю, что по условиям данного мысленного эксперимента, наши прямые, образованные лазерами, идеально прямые, простираются бесконечно, а следовательно и точка на их пересечении, по логике, должна при раздвигании лазеров, двигаться бесконечно... Но, вот мы ещё на микрон сдвинули наши стороны треугольника и, вуа ля! Оба угла стали равны 90 градусам, а стороны стали параллельны вместе с исчезновением точки пересечения (рис. 7).
Рис. 7. Два прямых угла образовали две параллельные линии, разорвав треугольник.
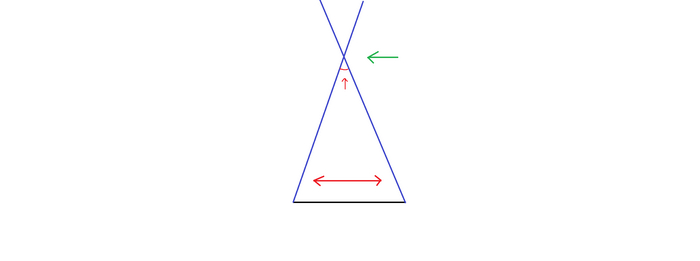
Здесь также следует отметить любопытную деталь, что верхний угол у нас постоянно уменьшался, но (вдруг кому пригодится эта деталь) через нуль он так и не прошёл. Откуда я это взял? Всё просто. Верхний угол треугольника мог бы быть нулевым, при условии, что обе стороны треугольника лежали бы одна на другой, то есть основание треугольника было бы нулевым. Но у нас есть условное основание (рис. 8). И если оно не нулевое, то и верхний угол, перед тем, как перестать существовать, не мог пройти через нуль.
Рис. 8. Основание имеется.
Вопрос, как же возможен данный парадокс?
Лично я пришёл к единственной гипотезе, которая состоит в том, что даже в цифровом мире, есть какой-то предел счисления, который мы называем условной бесконечностью, однако, по факту бесконечностью не являющийся.
Я пытался задать этот вопрос многим, кого считал сильными в математике, информатике и других науках. К сожалению среди моих знакомых и коллег нет математиков профессорского уровня, а поэтому никто из них не дал ответ, откуда берётся данный парадокс. Поэтому, теперь, если здесь есть кто-то кто имеет познания в данной области, буду рад прочитать ваши комментарии.
Спасибо если дочитали до конца! Заранее извиняюсь, если где был не точен в математических терминах, так как я всё же гуманитарий. ))
