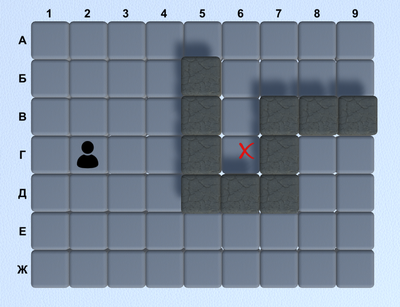
Поиск пути в играх. Алгоритм поиска пути A*
В своё время долго и упорно разбирал различные алгоритмы поиска путей для различных задач. Сейчас, во время отпуска, решил сделать доброе дело и поделиться накопленными знаниями.
В видео постарался разжевать всё так, чтобы стало понятно даже юзеру с нулевым знанием темы и программирования.
Надеюсь, что это будет кому то полезным.

Лига Разработчиков Видеоигр
9K постов23.2K подписчиков
Правила сообщества
ОБЩИЕ ПРАВИЛА:
- Уважайте чужой труд и используйте конструктивную критику
- Не занимайтесь саморекламой, пишите качественные и интересные посты
- Никакой политики
СТОИТ ПУБЛИКОВАТЬ:
- Посты о Вашей игре с историей её разработки и описанием полученного опыта
- Обучающие материалы, туториалы
- Интервью с опытными разработчиками
- Анонсы бесплатных мероприятий для разработчиков и истории их посещения;
- Ваши работы, если Вы художник/композитор и хотите поделиться ими на безвозмездной основе
НЕ СТОИТ ПУБЛИКОВАТЬ:
- Посты, содержащие только вопрос или просьбу помочь
- Посты, содержащие только идею игры
- Посты, единственная цель которых - набор команды для разработки игры
- Посты, не относящиеся к тематике сообщества
Подобные посты по решению администрации могут быть перемещены из сообщества в общую ленту.
ЗАПРЕЩЕНО:
- Публиковать бессодержательные посты с рекламой Вашего проекта (см. следующий пункт), а также все прочие посты, содержащие рекламу/рекламные интеграции
- Выдавать чужой труд за свой
Подобные посты будут перемещены из сообщества в общую ленту, а их авторы по решению администрации могут быть внесены в игнор-лист сообщества.
О РАЗМЕЩЕНИИ ССЫЛОК:
Ссылка на сторонний ресурс, связанный с игрой, допускается только при следующих условиях:
- Пост должен быть содержательным и интересным для пользователей, нести пользу для сообщества
- Ссылка должна размещаться непосредственно в начале или конце поста и только один раз
- Cсылка размещается в формате: "Страница игры в Steam: URL"