1 пост-ответ
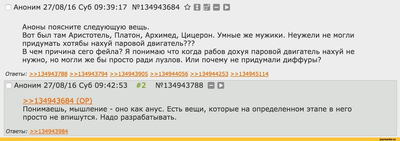
От лица всех математиков заявляю, что "слово Диаметр" применимо к любым множествам в метрическом пространстве и означает наибольшее расстояние между парой точек множества. Конкретно у квадрата диаметр - это диагональ.
раскрыть ветку (116)
От лица всех инженеров радуюсь, что миром правят не математики. А мы)) Ужо прибавили бы вы стране угля энтропии в жизни с таким подходом))
раскрыть ветку (38)
раскрыть ветку (7)
раскрыть ветку (4)
раскрыть ветку (3)
Да мы и так без злобы, да вон всё равно набежали защитнички без юмора. Всерьёз чего-то убеждают, будто математик сам ответить не может
Работодатель: Назовите вашу главную слабость.
Кандидат: Я даю семантически корректные, но практически неприменимые ответы на вопросы.
Работодатель: Могли бы вы привести пример?
Кандидат: Да, мог бы.
А то! Но обыватель-то запутается сам или, что быстрее, запутает того, кто шарит. Если вдруг усвоит. И - опа! - плюсик в хаос
математика - не наука as is.это в первую очередь язык, без которого ты сразу начнешь управлять не миром, а 8 миллиардами слепых котят, которые не в состоянии собрать даже сельский туалет, куда уж там ракеты или томографы. Притча о Вавилонской башне станет актуальной, как никогда. так что может быть миром и не правят математики, но им абсолютно точно правит математика. хотя если уходить глубже, то есть еще и философия науки.
раскрыть ветку (13)
раскрыть ветку (9)
Физика- описание законов, математика - тот язык, на котром приходится описывать, хотя и жестами иногда справляются...)
раскрыть ветку (8)
Причем описали так, как поняли, помашем Ньютону. Чисто Гоблинский перевод вселенского замысла.
раскрыть ветку (7)
да и не описание законов это, а описание явлений. Человечество даже близко еще не подобралось к законам, но некоторые модели строить научилось. И какие претензии к Ньютону? )
раскрыть ветку (6)
ну кроме того что он сектант был, никаких. до квантмеха он бы точно в свои годы не дошел. это просто к тому, что явления природы понимаются ровно настолько, насколько их можно изучить в конкретный период времени.
раскрыть ветку (5)
Ну так то конечно не дошел бы, но от него и не требовалось.
В очень широком диапазоне допущений ничего продвинутее законов Ньютона так то и не требуется, по-хорошему, так что чувак по истине гениальный был
раскрыть ветку (4)
бесспорно.для любой задачи, с которой реально потребутся столкнуться не физику - классической механики достаточно.
раскрыть ветку (3)
Так, падажжите, миром правит математика или философия? Просто мнений я за свою жизнь услышал много, а верить им всё труднее и труднее.
Мне очень скромно кажется, что миром правят-таки люди - существа, сумевшие допетрить до математики, физики, химии и всех прочих разных наукоинструментов, существующих поныне и сумевших сделать хорошо там, где плохо.
раскрыть ветку (1)
А вот тут в зависимости от того как вы видите мир. По идее мир можно описать и математически, и философски. По идее математику не изобретают, а открывают, то есть она существует независимо от человека. С другой стороны язык не может существовать, если на нем никто не говорит. Физика при этом очевидно существует без человека, хотя тут опять же встаёт вопрос о том, существует ли мир без наблюдателя. С философией ещё интереснее - изобретены ли правила научного исследования, типа наблюдение, эксперимент, анализ итд, или открыты - тот ещё вопрос для рассуждения. Так что не все так однозначно, сама я дочь метаматематика
раскрыть ветку (2)
Не соглашусь, был бы)) Бабушка в глухой татарской деревне слова "геометрия" могла не слышать никогда, а красота...она в её умелых руках)
раскрыть ветку (1)
Вообще-то, у инженеров, как правило есть высшее техническое образование, т.е. они проходят математические курсы с определением слова диаметр.
что миром правят не математики. А мыНу дык, инженер - это ведь не только старый мужик в берете, который на заводе выпиливает что-то на станке через такую-то мать. Большая часть современных технологий требует именно фундаментальных работ в области физики и математики. Компьютеры, космос, машинное обучение появились явно не без математики.
раскрыть ветку (10)
Инженер - это вообще не старый мужик в берете, который на заводе выпиливает что-то на станке через такую-то мать! Что за ересь?
И да, инженеры изучают высшую математику (мы 4 семестра учили), но множества в метрическом пространстве - это какая-то совсем другая математика.
раскрыть ветку (2)
Инженер - это вообще не старый мужик в берете, который на заводе выпиливает что-то на станке через такую-то мать! Что за ересь?
Вот именно! Я отвечал тому человеку выше. Подумал, что, возможно, в его представлении инженеры, может, выглядят так?
На деле, я сам работал на должности инженера. И не на заводе за станком, а за компом. И да, инженеры изучают высшую математику (мы 4 семестра учили), но множества в метрическом пространстве - это какая-то совсем другая математика.
Хз, у нас это было в матане. И многомерные пространства, и частные производные. Как без этого проходить термодинамику в техническом вузе - непонятно.
раскрыть ветку (1)
Инженер всё это (в силу своей специализации) понимает и практикует ровно в той степени, в какой необходимо и достаточно. И всё, в рамках практических задач - на этом хорош! Будет недостаточно - сам будет искать новое знание. Математик даёт ему это знание, иначе говоря, инструмент и, возможно, методику к тому инструменту, и всё, дальше ему лучше не вмешиваться
раскрыть ветку (6)
Нуу, это сильно условно всё. Никто не запрещает инженеру проводить научную работу, защищать кандидатскую и докторскую. Да, даже и без этого, никто не мешает инженеру читать что нового появилось/появится в его области или смежных.
Либо, мы мы по-разному понимаем слово инженер.
Конкретно определение диаметра, как я думал, может пройти любой студент технического вуза, что в Бакалавриате, что на Специалетете. Лично я проходил.
Я слегка триггернул на предложении миром правят не математики. А мы
Я сам работал на должности инженера и не понял юмора. То ли это самоирония от лица как бы местечкового инженера, который самый главный у себя в закутке.То ли, это камень в огород задротов-математиков, которые просчитывают у себя в абстрактных моделях сверических коней в вакууме, а на деле реальные пацаны-инженеры решают все проблемы по-мужски и не выпендриваются бесполезными хреновинами. :)
раскрыть ветку (5)
И то, и другое. И ещё пара тому объяснений есть. Но, честно говоря, уже хочу предложить свернуть вотэтовотвсё. Смотрю, нарвался на человека без юмора. Хотя...чего я хотел от человека, работавшего (именно так, в прошедшем) на должности инженера. Дружище, инженер - это не должность и не квалификация в дипломе. Это образ мышления, а может, и жизни. Как у медиков: либо ты эскулап до мозга костей без всяких условностей, либо нет.
раскрыть ветку (3)
Ээх, жаль, жаль. Я удивился, прочитав твой коммент, думал, ты объяснишь, что хотел этим сказать.
А оказалось, что вы - Д'Артаньян, а я - тупой человек, без юмора. Да ещё и предатель всего Содружества Инженеров (как выяснилось из моего коммента). Очень жаль.
А оказалось, что вы - Д'Артаньян, а я - тупой человек, без юмора. Да ещё и предатель всего Содружества Инженеров (как выяснилось из моего коммента). Очень жаль.
раскрыть ветку (2)
Нет, не предатель. Скорее, НЕинженер. Не знаю, может, Водитель, Математик тот же, Учитель, Моряк, Руководитель, Клерк или Торговец, да и не важно это. Но не Инженер, только и всего. Такова данность. Не плохо это и не хорошо. Ровно
Ну а я да, конечно, д´Артаньян. Как и всякий из нас
Ну а я да, конечно, д´Артаньян. Как и всякий из нас
раскрыть ветку (1)
Блиин. Как же печально, что меня лишили звания Инженера вот так вот, в комментариях Пикабу. Причём, человек, который, по-видимому, забивал на учёбу в вузе и считает, что Настоящий Инженер должен класть прибор на любые науки. Зато свято верет в своё потрясающее чувство юмора. Как же это драматично-то.
раскрыть ветку (1)
Ну почему же? Это мы его придумали, чтобы люди чувствовали разницу между ней, родимой, и отверстием)
Только не наибольшее расстояние, а супремум расстояния. Т.к. диаметр есть и у открытых множеств, граница которых им не принадлежит.
раскрыть ветку (2)
Стесняюсь спросить, а отрезок соединяющий противоположные точки параллельных сторон это, г-споди прости, хорда квадрата?
раскрыть ветку (49)
раскрыть ветку (45)
Видишь ли, евреям запрещено произносить имя господа вслух. Оттуда и пошло ироничное подражание речи еврея, где сознательно нюопускаеттся одна из букв: Б-г, г-подь. Начали и развили тему кащениты в далёких 2000-ых годах...
Ваш личный дипломированный интернет-мемолог на своей шхуне.
Ваш личный дипломированный интернет-мемолог на своей шхуне.
раскрыть ветку (31)
Так у православных тоже самое и они сознательно эти буквы пропускают. При этом думают "бог" и "господь" это имена, что очень странно, ну а имя они собственно и не знают, скорее всего.
раскрыть ветку (25)
Повторюсь, это всего лишь один из мемасов, плотно засевших в интернет сленг, да так, что уже и изначальное значение и суть употребления потерялись.
Хотя, ккащениты были милыми, но кусачими. До сих пор фраза "ви таки антесимит и говорите так потому щто я г'еврей?" почему-то вызывает море лулзов, особенно в связи с БЛМ.
Хотя, ккащениты были милыми, но кусачими. До сих пор фраза "ви таки антесимит и говорите так потому щто я г'еврей?" почему-то вызывает море лулзов, особенно в связи с БЛМ.
раскрыть ветку (5)
раскрыть ветку (4)
Видите ли, ввиду некоторых принятых в нашей стране законов, я предпочитаю иногда писать именно так, потому что не хочу, чтоб меня привлекли за оскорбление чувств верующих по причине "упоминал имя Господа в суе". Ну его нахер.
раскрыть ветку (2)
Таки имена. Имена нарицательные. И если вы общаетесь с человеком, чья вера известна, вы точно знаете, о каком господе боге он говорит. И с точки зрения языка все правильно.
раскрыть ветку (18)
раскрыть ветку (14)
раскрыть ветку (8)
раскрыть ветку (7)
раскрыть ветку (6)
Ну это Вы доебались, сударь. Просто мой вариант звучит почти так же, но имеет смысловую нагрузку. Да и если ещё больше доебаться, то первоначальный вариант «Колобог».
раскрыть ветку (1)
раскрыть ветку (3)
раскрыть ветку (2)
Вот вообще шокировало. Я об этом альбоме писала колонку в ежемесячном электронном журнале, когда он только вышел и выпуск был посвящён Хэллоуину. А сейчас оказывается, что прошло уже 7 лет и журнала нет давно, и творческий коллектив распался. Грустно как-то.
раскрыть ветку (1)
@Vedist, благодаря вам, я задумалась связаться с главным редактором и заняться распечаткой всех выпусков и рассылкой участникам коллектива. Спасибо! Думаю, из этого получится добрая память.
раскрыть ветку (2)
Если у бога нет имени собственного, а только нарицательное, то оно и становится по сути для него собственным. Так как в данных обстоятельствах и в данном языке он единственный объект называния этим словом. Поэтому и в христианстве он пишется с большой буквы. Есть «бог» как нечто общее, а есть «Бог», тот самый, их единственный. Это с филологической точки зрения.
раскрыть ветку (1)
Так это если нет собственно, а в данном случае думаю нарицательное употребляется, именно потому, что собственное верующий произносить нельзя. Так зачем же ещё и в нарицательном пропускать буквы? Тем более, что пропускают только в тексте, а в устной речи вполне спокойно произносят.
Я когда то думал, что это делается, чтобы страницы не индексировались поисковиком по этому слову.
ещё комментарии
раскрыть ветку (4)
Хочется позвать модератора, но еще больше хочется, чтобы вам заслуженно наставили минусов. Ибо пикабу должен знать своих токсичных героев.
раскрыть ветку (2)
ещё комментарии
ещё комментарии
это малый диаметр.
хорда квадрата меньше малого диаметра (например, соединяет точки на соседних сторонах)
хорда квадрата меньше малого диаметра (например, соединяет точки на соседних сторонах)
раскрыть ветку (2)
Кажется понял. Тогда отрезок, соединяющий две точки на одной стороне это, упаси -ллах, дуга квадрата, так?
раскрыть ветку (1)
Да, но слово Дуга употребляется к заведомо непрямым линиям.
А так - да, дуга.
Кстати, сектор квадрата тоже может быть квадратом.
А вот сектор круга (кроме 2п рад) - нет :)
А так - да, дуга.
Кстати, сектор квадрата тоже может быть квадратом.
А вот сектор круга (кроме 2п рад) - нет :)
Математика, конечно, царица наук и все такое, но вряд ли уместно переносить понимание узкопрофессиональных терминов на все случаи жизни.
раскрыть ветку (5)
На натуральных числах нету одной определённой метрики. Если брать Евклидову, то диаметр неопределён/ бесконечен. Если брать какую-нибудь p-адическую метрику, то 1. Учитывая, что если d(x,y) метрика, то A*d(x,y) тоже метрика, то понимаем, что диаметр может быть любым положительным числом.
раскрыть ветку (1)
В каком-то там пространстве, числовая прямая свернута в круг, и минус бесконечность равна бесконечности. В ней диаметр натуральных чисел равен нулю (или единице,лень думать)
раскрыть ветку (1)
Диаметр — наибольшее возможное расстояние между элементами множества. Контрпример: расстояние между числами 1 и 3 равно 2. Следовательно диаметр точно не равен нулю или единице.
Однако должен сказать, что необходимо определить, что именно подразумевается под расстоянием. Наиболее очевидное и простое: модуль разности, ибо модуль дается ещё в школьной программе, причем именно как расстояние от числа до нуля на числовой прямой. Я исходил именно из такого "расстояния".
Если на нём не задавать метрику, то понятие диаметра бессмысленно. Если задать метрику в виде, например, модуля разности, то будет бесконечность, т.к. само множество бесконечно
раскрыть ветку (14)
Нет, это не так.
Диаметр множества получается так - перебираются все пары точек. Для каждой пары точек считается расстояние между ними. Среди этих расстояний берётся максимальное. Это и будет диаметром.
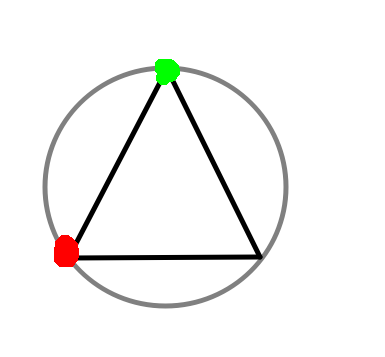
Например, для любого непрямоугольного треугольника - его диаметр будет меньше диаметра описанной окружности.
раскрыть ветку (12)
Нет. Представь треугольник с ну очень тупым углом. Пусть этот угол стремится к 180,тогда диаметр окружности, в которую он вписан, стремится к бесконечности. В то время как максимальное расстояние между точками равно самой длиной стороне треугольника.
раскрыть ветку (2)
...которая тоже стремится к бесконечности. Вы тут своим пределом только неопределенность создали)
Но суть ясна. У любого непрямоугольного треугольника все стороны меньше диаметра опис. окружности. Ближайшее доказательство - теорема синусов.
Вы правы, для треугольника условие "вписанности" в окружность - касание всех трёх углов. В этом случае диаметр окружности будет больше длиной стороны для треугольника с углом, близким к 180.
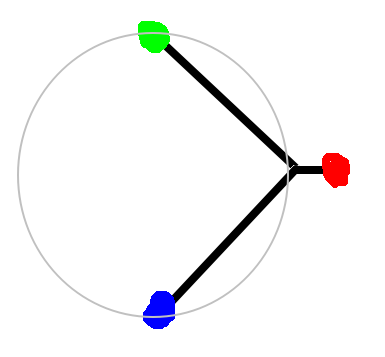
Нет. Вот контрпример. Фигура - три чёрных отрезка. Наибольшее расстояние между зелёной и синей точкой, но красная точка не попадает внутрь соответствующей окружности.
Диаметр - не больше диаметра описанной окружности, но не обязательно равен.
раскрыть ветку (8)
раскрыть ветку (7)
Блин, господа минусующие, ну возьмите вы обыкновенный треугольник. Диаметр треугольника, равный длине его стороны, очевидно, меньше диаметра окружности, так как это хорда, не проходящая через центр. Всё ещё не верите? Это же элементарная геометрия.
раскрыть ветку (1)
так в этом и суть данного контрпримера. Диаметры фигуры и окружности равны, но при этом фигура не помещается в окружность. Значит, не для всех фигур диаметр фигуры = диаметру описанной окружности
Вы не поняли. Да и он сам не оч удачно изобразил. Если множество - это 3 этих точки (красная, синяя и зелёное), то диаметром этого множества будет расстояние от синей до зелёной. Можно описать окружность вокруг треугольника с вершинами в этих точках, но её диаметр не будет равен нашему диаметру множества.
Ты абсолютно прав. Я показал окружность, у которой диаметр совпадает с диаметром фигуры. Оказалось, что фигура в такую окружность не вписывается. Отсюда делаем вывод, что диаметр фигуры меньше диаметра описанной окружности.
раскрыть ветку (2)
раскрыть ветку (1)
Конкретно в данном случае - строго меньше. То, что в общем случае меньше либо равен, я писал комментарием выше.