Набор из 12 необычных логических задач
Представляю вам 12 логических задач, на которые вы все равно не обратите внимания и просто пройдете мимо
1. Непутевые разбойники
Пять разбойников делят добычу в 50 золотых. Делят добычу они следующим образом:
1) Самый старший из них предлагает вариант дележа добычи.
2) Все (включая самого старшего) голосуют.
3) Если за этот вариант дележа проголосует более половины разбойников, то на этом дележ добычи заканчивается.
4) В противном случае все остальные убивают самого старшего разбойника и дележ начинается снова с пункта 1).
Каждый разбойник в первую очередь хочет сохранить себе жизнь, на втором месте в его списке приоритетов стоит получение как можно большей доли.
Каков будет результат дележа?
2. Разрыв мозга
Какое из сочетаний слов имеет смысл:
А) Приплыло ходила.
Б) Приползло бегала.
В) Пришло ползала.
Г) Прибежало плавала.
3. Хорошими делами прославиться нельзя...
Чебурашка и Шапокляк поедают ящик апельсинов. За один ход Шапокляк может либо съесть один хороший апельсин, либо заменить два хороших апельсина на два гнилых, Чебурашка может либо съесть два хороших апельсина, либо съесть один хороший и выкинуть один гнилой. Первым ходит Чебурашка. Проигрывает тот, кто не сможет сделать ход.
Кто выигрывает при правильной игре, если изначально в ящике было n хороших и ни одного гнилого апельсина?
4. Математическая магия
Каковы три последние цифры числа 7^9999?
5. Скучный ребус
Что обычно не помещают в комнату?
6. Рыцари Смаллиана
Перед нами снова три островитянина А, В и С, о каждом из которых известно, что он либо рыцарь, либо лжец. Двое из них (А и В) высказывают следующие утверждения:
А: Мы все лжецы.
В: Один из нас рыцарь.
Кто из трех островитян А, В и С рыцарь и кто лжец?
7. Головоломка Слотобера — Граатсмы
Требуется упаковать шесть блоков 1×2×2 и три блока 1×1×1 в куб со стороной 3. Решение головоломки единственно (с точностью до зеркальных отражений и поворотов).
8. Возвращение Рыцарей Смаллиана
А, В и С - либо рыцари, которые всегда говорят правду, либо лжецы, которые всегда лгут. Предположим, что незнакомец задал А другой вопрос: "Сколько рыцарей среди вас?" И на этот вопрос А ответил неразборчиво. Поэтому незнакомцу пришлось спросить у В: "Что сказал А?" В ответил: "А сказал, что среди нас один рыцарь". И тогда С закричал: "Не верьте В! Он лжет!" Кто из двух персонажей В и С рыцарь и кто лжец?
9. Мтемтическя здч
Петя и Вася (начинает Петя) по очереди стирают буквы из набора "МАТЕМАТИЧЕСКАЯ ЗАДАЧА". За один ход разрешается стереть или ровно одну букву, или все одинаковые буквы. Выигрывает тот, кто сотрет последнюю букву. Кто выиграет в этой игре и какой должна быть выигрышная стратегия?
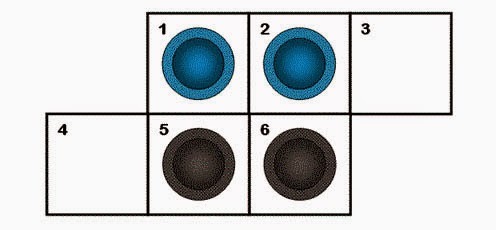
10. Черные против синих
Поменяйте местами синие и черные фишки. Разрешается двигать фишки только на смежное пустое место.
11. Очередная математическая магия
Докажите, что:
а) число 11...1211...1, состоящее из 100 единиц слева и 100 единиц справа от единственной двойки, является составным;
б) число 11...1122...22, состоящее из 100 единиц и 100 двоек есть произведение двух последовательных целых чисел.
12. Неожиданная встреча
Встретились как-то два друга.
— Привет!
— Привет!
— Как дела?
— Хорошо. Растут два сына, дошкольника.
— А сколько им лет?
— Произведение их возрастов равно числу голубей около этой скамейки.
— Этой информации мне недостаточно!
— Старший похож на мать.
— Вот теперь я знаю ответ на свой вопрос!
Сколько лет обоим сыновьям?
Послесловие
Если вы уже сталкивались с какой угодно любой задачей, которая тут находится, и знаете ответ просто потому что знаете, прошу не рассказывать о нем в комментариях. Дайте людям подумать самим. Если вы догадались до ответа с помощью логического мышления и остроты ума, можете обсудить задачу в комментариях.
Ответы выложу через 48 часов в комментарии