TheCakeIsALie5

Представляю вам новую версию теста Джимми Пропа, который, если кто не знает, направлен на определение способности к решению самоссылающихся задач.

Вопросов в этом тесте 12, решение теста единственное, и, скорее всего, решение займет у вас несколько часов. На каждый из вопросов совершенно точно можно найти правильный ответ.

Я не знаю, что еще написать. Дерзайте, что ли.

1. Количество вопросов с ответом "A" равно только количеству вопросов с ответом:

А) B

B) C

C) D

D) E

E) Все перечисленные

2. Единственные два соседних вопроса с одинаковыми ответами это:

А) 1 и 2

B) 2 и 3

C) 3 и 4

D) 4 и 5

E) 5 и 6

3. Ответ на вопрос 8:

А) C

B) A

C) E

D) D

E) B

4. Ответ на предыдущий вопрос:

А) не А

B) не В

C) не С

D) не D

E) не E

5. Книга, объединяющая математику, музыку и искусство, называется "Гёдель, Эшер, ..."

A) Бах

B) Ба-бах!

C) Ба-ба-бах!

D) Ба-ба-ба-ба-бах!!

E) Бум!!!

6. Ответы на вопросы с 6 по 8 образуют арифметическую прогрессию с шагом:

A) 2,718281...

B) 0

C) 1

D) 1

E) 2

7. Ответ на этот вопрос:

A) Состоит из четырех слов

B) Состоит из восьми слогов

C) Состоит из одиннадцати слогов

D) Состоит из двадцати шести букв

E) Все варианты верны

8. Ответ на вопрос 9:

А) C

B) E

C) B

D) D

E) A

9. Ответ на вопрос 3:

А) C

B) A

C) B

D) D

E) E

10. Единственный вопрос с четным номером и гласным ответом это:

A) 2

B) 4

C) 6

D) 8

E) 10

11. Количество вопросов с этим ответом:

A) 0

B) 1

C) 2

D) 3

E) 4

12. Выберите одно из верных утверждений:

A) Вы неверно решили тест

B) Вы верно решили тест

C) В этом тесте 12 вопросов

D) Вы молодец

E) Вы устали после прохождения теста

Представляю вам 11 сложных логических задач, которые вы просто обязаны решить

1. Богатый Петя

На Петином счету в банке лежит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов.

Какую максимальную сумму Петя может снять со счета, если других денег у него нет?

2. Стих

— Молчи, _____, —

Сказала _____:

В тебе _____ я,

Во мне до _____ я.

В этом стихотворении было пропущено четыре слова. Два последних называют числа. А какова разность этих чисел?

3. Петя, Вася, два ствола

Петя и Вася (начинает Петя) по очереди стирают буквы из набора "МАТЕМАТИЧЕСКАЯ ЗАДАЧА". За один ход разрешается стереть или ровно одну букву, или все одинаковые буквы. Выигрывает тот, кто сотрет последнюю букву. Кто выиграет в этой игре и какой должна быть выигрышная стратегия?

4. Непростой джаз, чешущий лимон

Джаз, лимон, непросто, чешущее. Какое ещё слово можно отнести в этот список?

(А) ящичек; (Б) элемент; (В) хочешь; (Г) клеймо; (Д) выгода.

5. Лечебница доктора Смолля и профессора Перро, часть 1

Все три следующие задачи взяты из книги Реймонда Смаллиана "Принцесса и тигр"

Однажды инспектора Крейга из Скотланд-Ярда срочно откомандировали во Францию для проверки одиннадцати лечебниц для умалишенных, где, по слухам, дела обстояли не слишком-то хорошо. В каждой из лечебниц единственными обитателями были пациенты и врачи - причем последние составляли весь персонал этих медицинских учреждений. Каждый обитатель лечебницы, будь то пациент или доктор, либо находился в здравом уме, либо был лишен рассудка.

Кроме того, нормальные обитатели были абсолютно нормальны и на сто процентов уверены в том, что они говорят; они твердо знали, что все истинные утверждения действительно являются истинными, а все ложные - на самом деле ложными. В то же время безумные обитатели лечебниц придерживались совершенно противоположных представлений: все истинные утверждения они считали ложными, а все ложные утверждения - истинными. Наконец, надо полагать, что все обитатели лечебниц во всех случаях остаются честными - они всегда верят в то, что говорят.

В первой же лечебнице, которую посетил Крейг, он беседовал по очереди с двумя обитателями, которых звали Джонс и Смит.

- Не могли бы вы рассказать мне, - обратился инспектор к Джонсу, - что вам известно о мистере Смите?

- Вам следовало бы называть его доктор Смит, - поправил Джонс, - Ведь это один из врачей нашей больницы.

Позже Крейг задал Смиту вопрос:

- Что вам известно о Джонсе? Он здесь пациент или доктор?

- Он пациент, - ответил Смит.

Поразмыслив некоторое время, инспектор смекнул, что дела в этой лечебнице и в самом деле идут не блестяще: либо один из докторов лишился рассудка и, значит, ему не следует продолжать работу в больнице для умалишенных, либо, что еще хуже, один из пациентов является нормальным человеком и вообще не должен находиться здесь. Как Крейг догадался об этом?

6. Лечебница доктора Смолля и профессора Перро, часть 2

В следующей лечебнице Крейг имел беседу с четырьмя ее обитателями А, В, С и D. А считал, что психическое состояние В и С одинаково. В считал, что психическое состояние А и D одинаково. Кроме того, на вопрос инспектора, заданный С: "Являетесь ли вы и D оба докторами?", С ответил: "Нет". Все ли обстоит благополучно в данной лечебнице?

7. Лечебница доктора Смолля и профессора Перро, часть 3

Последней лечебницей руководили два известных врача - доктор Смолль и профессор Перро. При этом здесь неукоснительно придерживачись следующих правил. Если обитатель лечебницы считал, что он является пациентом, то его называли чудаком. Если же все пациенты считали, что данный обитатель чудак, а ни один из врачей его за чудака не принимал, то такого обитателя больницы было принято именовать оригиналом. Вдобавок Крейгу удалось выяснить еще два обстоятельства: 1) по крайней мере один из обитателей больницы был вполне нормальным и 2) у каждого обитателя лечебницы имелся близкий друг, и если обитатель А считает, что обитатель В является оригиналом, тогда близкий друг этого А полагает, что В - пациент.

Вскоре после этого открытия инспектор Крейг решил в частном порядке побеседовать с больничным руководством в лице доктора Смолля и профессора Перро. Разговор с первым из них протекал так.

Крейг. Скажите, доктор Смолль, все ли врачи в вашей больнице в здравом уме?

Смолль. Я в этом абсолютно уверен.

Крейг. А как обстоят дела с пациентами? Все ли они безумны?

Смолль. По крайней мере один из них.

Крейга поразил последний ответ - уж очень он был осторожным. Конечно, если все больные в лечебнице лишены рассудка, то утверждение, что хоть один из них безумен, представляет собой несомненную истину. Но почему доктор Смолль был так сдержан в своем утверждении?

Затем Крейг побеседовал с профессором Перро; на этот раз разговор протекал следующим образом.

Крейг. Доктор Смолль утверждает, что по крайней мере один из здешних пациентов безумен. Это правда, не так ли?

Профессор Перро. Конечно, правда. Все пациенты тут безумны! Чем же мы руководим, по-вашему?

Крейг. А как обстоят дела с врачами? Все ли они нормальны?

Профессор Перро. По крайней мере один из них нормален.

Крейг. А что вы скажете о докторе Смолле? Он-то хоть нормален?

Профессор Перро. Ну, разумеется! Как вы смеете задавать мне такой вопрос?

Вопрос: как обстоят дела в лечебнице доктора Смолля и профессора Перро?

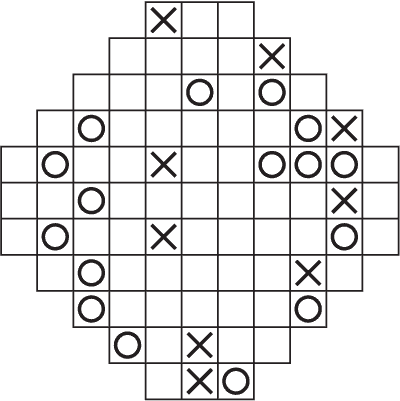
8. Крестики-нолики

Заполните поле крестиками и ноликами, так чтобы ни в одном горизонтальном, вертикальном или диагональном ряду не было более трех одинаковых знаков подряд:

9. Бесконечный коридор

В узком 100-метровом Стэнфордском коридоре, шириной в одного человека, стоят 25 узников на некотором расстоянии друг от друга. У всех завязаны глаза. По команде они начинают двигаться. Кто-то налево, кто-то направо. Если они сталкиваются друг с другом, то разворачиваются и идут в другую сторону. Если доходят до конца коридора — выходят на свободу, и их можно больше не учитывать. Скорость каждого — 1 метр в секунду. Время на разворот не считается. Через какое минимальное время все узники гарантированно покинут коридор?

10. Кровь и бетон

Предположим Вам надо повалить бетонную стену длиной в 20 метров, высотой в 3 метра и весом в 3 тонны. Как вы выполните эту задачу, если в вашем распоряжении нет абсолютно никаких инструментов?

11. Ну ты животное!

Во всех данных словах, кроме одного, можно переставить буквы так, что получатся названия животных. Кроме какого?

(А) банка; (Б) крона; (В) скала; (Г) шкала; (Д) шпала.

Послесловие

Если вы уже сталкивались с какой угодно любой задачей, которая тут находится, и знаете ответ просто потому что знаете, прошу не рассказывать о нем в комментариях. Дайте людям подумать самим. Если вы догадались до ответа с помощью логического мышления, можете обсудить задачу в комментариях.

Ответы выложу через 48 часов в комментарии

Представляю вам 12 логических задач, на которые вы все равно не обратите внимания и просто пройдете мимо

1. Непутевые разбойники

Пять разбойников делят добычу в 50 золотых. Делят добычу они следующим образом:

1) Самый старший из них предлагает вариант дележа добычи.

2) Все (включая самого старшего) голосуют.

3) Если за этот вариант дележа проголосует более половины разбойников, то на этом дележ добычи заканчивается.

4) В противном случае все остальные убивают самого старшего разбойника и дележ начинается снова с пункта 1).

Каждый разбойник в первую очередь хочет сохранить себе жизнь, на втором месте в его списке приоритетов стоит получение как можно большей доли.

Каков будет результат дележа?

2. Разрыв мозга

Какое из сочетаний слов имеет смысл:

А) Приплыло ходила.

Б) Приползло бегала.

В) Пришло ползала.

Г) Прибежало плавала.

3. Хорошими делами прославиться нельзя...

Чебурашка и Шапокляк поедают ящик апельсинов. За один ход Шапокляк может либо съесть один хороший апельсин, либо заменить два хороших апельсина на два гнилых, Чебурашка может либо съесть два хороших апельсина, либо съесть один хороший и выкинуть один гнилой. Первым ходит Чебурашка. Проигрывает тот, кто не сможет сделать ход.

Кто выигрывает при правильной игре, если изначально в ящике было n хороших и ни одного гнилого апельсина?

4. Математическая магия

Каковы три последние цифры числа 7^9999?

5. Скучный ребус

Что обычно не помещают в комнату?

6. Рыцари Смаллиана

Перед нами снова три островитянина А, В и С, о каждом из которых известно, что он либо рыцарь, либо лжец. Двое из них (А и В) высказывают следующие утверждения:

А: Мы все лжецы.

В: Один из нас рыцарь.

Кто из трех островитян А, В и С рыцарь и кто лжец?

7. Головоломка Слотобера — Граатсмы

Требуется упаковать шесть блоков 1×2×2 и три блока 1×1×1 в куб со стороной 3. Решение головоломки единственно (с точностью до зеркальных отражений и поворотов).

8. Возвращение Рыцарей Смаллиана

А, В и С - либо рыцари, которые всегда говорят правду, либо лжецы, которые всегда лгут. Предположим, что незнакомец задал А другой вопрос: "Сколько рыцарей среди вас?" И на этот вопрос А ответил неразборчиво. Поэтому незнакомцу пришлось спросить у В: "Что сказал А?" В ответил: "А сказал, что среди нас один рыцарь". И тогда С закричал: "Не верьте В! Он лжет!" Кто из двух персонажей В и С рыцарь и кто лжец?

9. Мтемтическя здч

Петя и Вася (начинает Петя) по очереди стирают буквы из набора "МАТЕМАТИЧЕСКАЯ ЗАДАЧА". За один ход разрешается стереть или ровно одну букву, или все одинаковые буквы. Выигрывает тот, кто сотрет последнюю букву. Кто выиграет в этой игре и какой должна быть выигрышная стратегия?

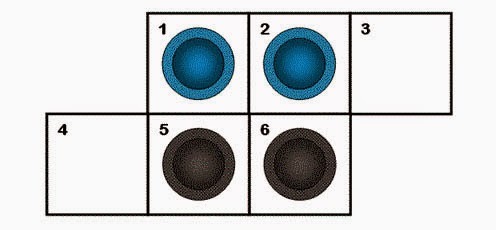
10. Черные против синих

Поменяйте местами синие и черные фишки. Разрешается двигать фишки только на смежное пустое место.

11. Очередная математическая магия

Докажите, что:

а) число 11...1211...1, состоящее из 100 единиц слева и 100 единиц справа от единственной двойки, является составным;

б) число 11...1122...22, состоящее из 100 единиц и 100 двоек есть произведение двух последовательных целых чисел.

12. Неожиданная встреча

Встретились как-то два друга.

— Привет!

— Привет!

— Как дела?

— Хорошо. Растут два сына, дошкольника.

— А сколько им лет?

— Произведение их возрастов равно числу голубей около этой скамейки.

— Этой информации мне недостаточно!

— Старший похож на мать.

— Вот теперь я знаю ответ на свой вопрос!

Сколько лет обоим сыновьям?

Послесловие

Если вы уже сталкивались с какой угодно любой задачей, которая тут находится, и знаете ответ просто потому что знаете, прошу не рассказывать о нем в комментариях. Дайте людям подумать самим. Если вы догадались до ответа с помощью логического мышления и остроты ума, можете обсудить задачу в комментариях.

Ответы выложу через 48 часов в комментарии

Не обращайте внимание на заголовок, он сделан лишь для привлечения вашего внимания. С другой стороны, задач тут так и так 13. Попытайтесь их решить, если сможете.

1. Место, которое нельзя называть

Вы сидите в самолете, впереди Вас лошадь, сзади автомобиль. Где Вы находитесь?

2. Король и шут

Когда-то давно, жил в одном дворце придворный шут, который пробовал себя в логике. И вот однажды шут принес королю две шкатулки.

На крышке первой было написано:

«Либо в этой шкатулке сидит злая лягушка, либо в шкатулке с ложной надписью сидит злая лягушка, но не оба одновременно».

На крышке второй было написано:

«Либо в этой шкатулке лежит золото, а в шкатулке с ложной надписью сидит лягушка, либо в этой шкатулке сидит злая лягушка, а в шкатулке с истинной надписью лежит золото».

И шут сказал королю: «В одной шкатулке сидит злая лягушка, в другой лежит золото; одна, и только одна из надписей истинна».

Какую шкатулку надо открыть королю?

А) Левую

Б) Правую

В) Не трогать шкатулки и просто бросить шута в темницу

3. Классическая задача с бесконечным поездом

Вы находитесь в поезде, состоящем из некоторого количества вагонов. Все вагоны сцеплены в кольцо, и в каждом есть лампочка, которую можно включать и выключать. В начальном положении лампочки в вагонах горят в случайном порядке. Как сосчитать количество вагонов? (пометок делать нельзя, все вагоны одинаковые и отличить один от другого, кроме как по лампочке, никак нельзя)

4. Числовой ребус

Буквами зашифрованы цифры. Разным буквам соответствуют разные цифры. Каким может быть наибольшее значение суммы?

ONE + DEUX = DREI

5. Непознанное и непознаваемое

29 ноября 2015 года логотип поисковой системы Google для российских пользователей выглядел так (за исключением небольшой детали, не показанной тут):

А что за деталь была скрыта?

А) пятиконечная звезда; 

Б) треугольник и квадрат;

В) две точки; 

Г) пчела; 

Д) корни у дерева.

6. Рыцари и лжецы, встреча 1

Путешественник вышел на дорогу, соединяющую город лжецов и город рыцарей. Он хочет узнать, в какой стороне находится каждый из городов. Какой вопрос он должен задать прохожему (не зная, рыцарь он или лжец), чтобы определить это?

7. Олив

Вставьте слово, пропущенное в цитате из «Писем русского путешественника» Н. М. Карамзина:

"Не бойтесь: быстрый луч света издали озаряет ваши глаза ― ещё несколько шагов, и вы опять в __________ мире, на берегу журчащей речки, среди прелестных ландшафтов."

А) сливочном; 

Б) подсолнечном; 

В) кукурузном;

Г) арахисовом; 

Д) машинном.

8. Задача выбора Уэйсона

Перед вами на столе лежат четыре карты, каждая из которых имеет число с одной стороны и цветную рубашку с другой. Карты лежат в следующем порядке: 3, 8, красная, коричневая. Сколько и каких карт надо перевернуть, чтобы проверить истинность следующего утверждения: если на карте изображено чётное число, то рубашка у карты красная?

9. Рыцари и лжецы, встреча 2

На острове, население которого составляют только рыцари, всегда говорящие правду, и лжецы, которые всегда лгут, находится НИИ. Каждый из его сотрудников однажды сделал два заявления:

а) В институте нет и десяти человек, которые работают больше меня.

б) По крайней мере сто человек в институте получают зарплату большую, чем моя.

Известно, что нагрузка у всех работников разная, как и зарплата. Сколько человек работает в НИИ?

10. Долгие скачки

У вас имеется 25 скаковых лошадей, среди которых требуется выбрать трех самых быстрых. К сожалению, вам запрещено пользоваться любыми измерениями для определения скорости лошади или времени забега.

Какое минимальное количество забегов потребуется провести, если в скачках одновременно могут участвовать только 5 лошадей?

11. Четыре четверки

Классика. Требуется получить с помощью записи четырех четверок все числа от 1 до 20. Разрешается использовать знаки сложения, вычитания, деления, умножения, квадратного корня и степени. Ах да, и факториал тоже можно.

12. Боги и лжецы

Есть три бога: A, B и C, которые являются богами истины, лжи и случая в произвольном порядке. Бог истины всегда говорит правду, бог лжи — всегда обманывает, бог случая может говорить и правду, и ложь в произвольном порядке. Требуется определить богов, задав 3 вопроса, на которые можно ответить «да» или «нет». Каждый вопрос задаётся только одному богу, но можно задавать одному богу более одного вопроса. Боги понимают язык, но отвечают на своём языке, в котором есть 2 слова «da» и «ja», причём неизвестно, какое слово обозначает «да», а какое «нет».

1) Можно задавать одному богу более чем один вопрос (поэтому другим богам может быть не задано ни одного вопроса вообще).

2) Каков будет следующий вопрос и кому он будет задан, может зависеть от ответа на предыдущий вопрос.

3) Бог случая отвечает «da» или «ja» на любой вопрос, на который можно ответить «да» либо «нет».

4) Нельзя задавать вопросы-«парадоксы», на которые можно ответить и «da» и «ja», или никак нельзя ответить (например, «Ты сейчас ответишь „da“?»). Это вызовет синий экран у бога и вселенная коллапсирует.

13. На злобу дня

Битву, изображённую на древней моза_ке, вы_грали во_ны Та_ланда. В скольких местах и где была пропущена буква 'й'?

Послесловие

Если вы уже сталкивались с какой угодно любой задачей, которая тут находится, и знаете ответ просто потому что знаете, прошу не рассказывать о нем в комментариях. Дайте людям подумать самим. Если вы догадались до ответа с помощью логического мышления и остроты ума, милости прошу, обсуждайте задачу в комментариях.

Ответы выложу через 48 часов в комментарии, или, если хотите, отдельным постом.

Ссылка на прошлый пост: http://pikabu.ru/story/mnozhestvo_mandelbrota_5071307

Ссылка на позапрошлый пост: http://pikabu.ru/story/fraktal_zhulia_5056476

В прошлый раз я тут выложил несколько гифок, красочно описывающих фрактал Мандельброта, и мне пришло в голову его немного модифицировать.

Как все мы знаем, множество Мандельброта обычно выглядит так

Как получается такая вещь? Для начала, небольшое отступление.

Данная плоскость, показанная на картинке - не та, которую обычно изучают в школе, а комплексная. Что это значит? То, что каждой точке на ней соответствует число (x + yi), где i - корень из -1. Да, из отрицательных чисел обычно нельзя извлечь корень, но математики те еще шутники, поэтому выдумали специальное обозначение для таких вот вещей.

Благодаря тому, что каждая точка на комплексной плоскости является еще и числом, с ней можно производить те обычные математические действия, какие невозможно совершать на обычной плоскости, как, например, умножение, возведение в квадрат, и так далее.

Так вот, для получения множества Мандельброта берем случайную точку В с координатами (х, у), и точку А с координатами (0, 0). Затем мы умножаем точку А саму на себя (получится опять же нулевая точка), а потом прибавляем к ней точку В.

Если полученная точка выходит за круг радиуса 2, тогда все шикарно. Если нет, то снова проделываем те же манипуляции: умножаем получившуюся точку саму на себя, прибавляем точку В, и снова проверяем. Чем больше проходов требуется, чтобы достичь границы заветного круга, тем ярче становится точка. Если точка вылетает из круга после одной итерации - она почти черная. Если и за тысячу проделанных действий не удалось улепетнуть - она синяя (ну или любого другого цвета, в зависимости от выбранной палитры, моего настроения и моей великолепной силы духа). Иногда точка вообще не может выбраться из круга - вот именно тогда она и принадлежит множеству Мандельброта.

Ладно, надеюсь, вы поняли. Если не поняли, то вот ссылка, которая точно все разъяснит:

http://sunandstuff.com/mandelbrot/about/

-----------------------------------------------------------------------------------------------

Немного математики, или как я получил уравнение для вывода этого чертового фрактала

В ролях: точка А в роли точки А, точка В в роли точки В, и мисс Мурпл в роли мисс Бурпл.

А если серьезно, то можете пропускать эту часть, если вам не интересна математика, и хочется посмотреть на интересные картинки. Для остальных же: пусть точка А имеет координаты (a, b), а точка В - (x, y). Тогда А будет равно a+bi, В равно x+yi.

А * А + В = (a+bi)*(a+bi) + (x+yi) = (a*a + 2*a*b*i + b*b*i^2) + x + yi =

(a*a + b*b*i^2 + x) + (2*a*b + y) * i =

(a*a - b*b + x) + (2*a*b + y) * i

Так как точка А имела координаты (a, b), и именно ее нам и надо преобразовать, получим:

a -> a*a - b*b + x

b -> 2*a*b + y

-----------------------------------------------------------------------------------------------

Извращения (осторожно! много тяжелых гифок!)

Для начала я решил немного поиграться с уравнениями. Недолго думая, я решил взять второе уравнение по модулю. И получил неожиданный результат.

a -> a*a - b*b + x

b -> abs(2*a*b + y)

Ничем не отличается от обычного Мандельброта, такие же красивые неповторяющиеся узоры. Кто как, а я вижу тут зайца и лебедя. Одновременно.

Затем я взял по модулю первое уравнение. И лучше бы я этого не делал.

a -> abs(a*a - b*b + x)

b -> 2*a*b + y

Нет, это не член. Кого я обманываю. Клубничку ставить?

Отчаявшись, я взял по модулю оба уравнения.

a -> abs(a*a - b*b + x)

b -> abs(2*a*b + y)

К своему удивлению, я получил офигенскую картинку с бесконечным количеством одних и тех же повторяющихся узоров.

Интересные наблюдения: если поставить модуль напротив x или y, то картинка просто станет симметричной относительно горизонтали или вертикали. Также бесполезно ставить минус напротив них, картинка после этого просто станет зеркальной.

Когда действия с модулями кончились, просто умножил второе уравнение на -1.a -> a*a - b*b + xb -> -2*a*b - y

Получил красивую трехпалую фигню, похожую на космический корабль снизу. Нет, это удивительно, я просто поменял знак уравнения, а какой эффект, это же просто ААаааааааа... Кхм. Я отвлекся.

Если поменять знаки только у первого уравнения, получится то же самое. Если поменять у обоих, получится... ни за что не догадаетесь. Множество Мандельброта.

Приступаем к самому вкусному. Тригонометрия. Синус, если точнее.

a -> sin(a*a - b*b + x)

b -> 2*a*b + y

Получилась интересная красивая модификация Мандельброта, из которой вырываются всполохи зеленого нечто, похожие на протуберанцы у Солнца.

То же самое, но косинус появляется у второго уравнения.

a -> a*a - b*b + x

b -> cos(2*a*b + y)

Как будто множество Мандельброта вывернули наизнанку. Или паутина с кучей дыр.

Прибавляем синус к первому уравнению, и модуль ко второму.

a -> sin(a*a - b*b + x)

b -> abs(2*a*b + y)

И снова вывернутый наизнанку Мандельброт. На этот раз узор отличается цветочностью и клиньями. Ну, все синусы чем-то таким грешат.

На этот раз я решил возвести изначальное уравнение в куб (то есть получится А * А * А + В).

a -> a*a*a - 3*a*b*b + x

b -> 3*a*a*b - b*b*b + y

Почти ничем не отличается от Мандельброта, кроме изначального узора на первом кадре

Пойдем дальше, зачем нам какие-то простые кубы? Давайте четвертую степень!

a -> a*a*a*a - 6*a*a*b*b + b*b*b*b + x

b -> 4*a*a*a*b - 4*a*b*b*b + y

Аналогично. Такой же узор можно встретить и в Мандельброте

Как можно заметить, количество выпирающих пупырышек увеличивается с каждым увеличением степени. Для второй степени (т.е. Мандельброта) - одна пупырка, для третьей степени - две, для четвертой степени - уже три пупырки. Но допустим, степеней будет восемь.

Кстати, если взять у пятой степени первое уравнение по модулю, получится лягушка. На первой картинке снизу видна обычная пятая степень, на второй - лягуха.

Если изменить второе уравнение, а не первое - лягуха будет смотреть налево, а не вверх.

Кажется, все, а то и так слишком много. Оставшиеся гифки выложу потом, а то сайт не резиновый.

Полученные модификации математической ценности не имеют (наверное). Зачем же все это, спросите вы?