Люблю такие задачи⁠⁠1

Это задача из ЕГЭ, решается, как оказалось, очень просто в три действия, но я, честно говоря не сразу догадался. Вот условие задачи (цитата):

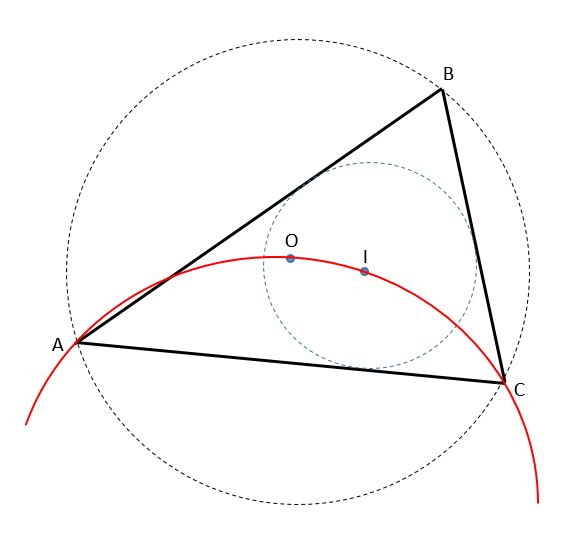
«В остроугольном треугольнике ABC центр описанной окружности (точка О), и центр вписанной окружности (точка I), а также вершины треугольника А и С лежат на одной окружности. Доказать, что угол ABC = 60°.»

Привожу чертеж для «удобства»:

Сразу хочу сказать, что чертеж не совсем верный, ведь описанная окружность и красная окружность, на которой лежат точки O, I, A и C должны были бы получится одного радиуса, в чем легко убедится, если начать построение с равностороннего треугольника, а потом сметить точку B по дуге BC вправо. Но в условии задачи ничего не сказано о радиусах окружностей.

В размышлениях, как точки могут делить окружность на дуги, родилась следующая задача:

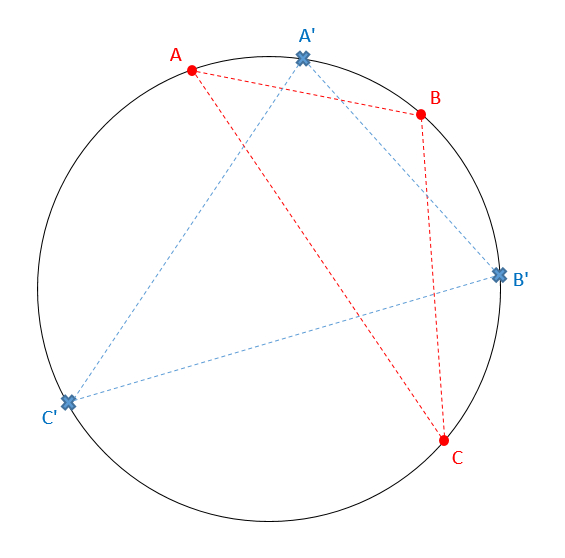
На окружности произвольным образом заданы три точки A, B и C. Можно представить себе какой-то произвольный треугольник ABC, вписанный в окружность. Три новых точки A’, B’ и С’ построим следующим образом: A’ – середина дуги AB, B’ – середина дуги BC, и C' – середина дуги AC. Заметим, что новый треугольник A’B’C’ уже больше похож на равносторонний.

Повторим такое построение несколько раз, и с увеличением количества итераций мы все точнее и точнее будем приближаться к равностороннему треугольнику. Требуется доказать сходимость алгоритма.