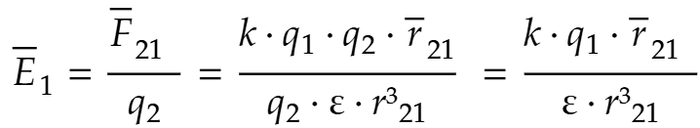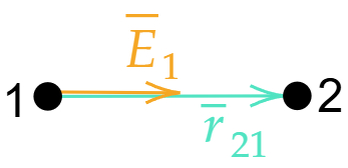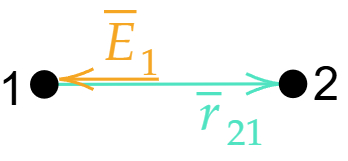fizikaVzametkah

Учимся понимать ФИЗИКУ так, чтобы не ты боялся ЕГЭ, а ЕГЭ боялся тебя.

На Пикабу 4 месяца 4 недели

поставил 3 плюса и 0 минусов

195 рейтинг 9 подписчиков 3 подписки 12 постов 0 в горячем

2 месяца назад

#Заметка 11. Потенциал электрического поля.Связь между напряженностью и напряжением для однородного электрического поля⁠⁠

Две основные характеристики электрического поля:
1. Потенциал (φ) - энергетическая характеристика поля
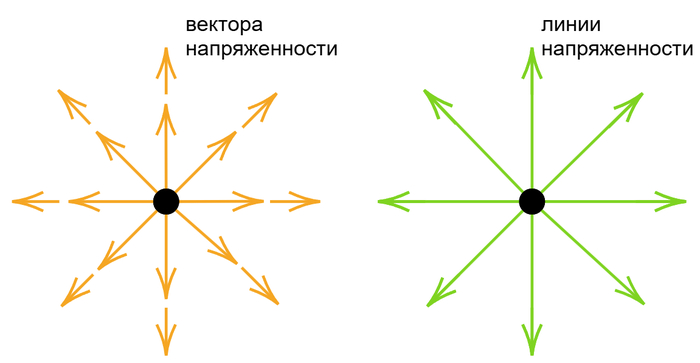
2. Напряженность (E) - силовая характеристика поля

Подробнее о напряженности - в отдельной заметке #Заметка9. О напряженности электрического поля. Сейчас разберем потенциал.

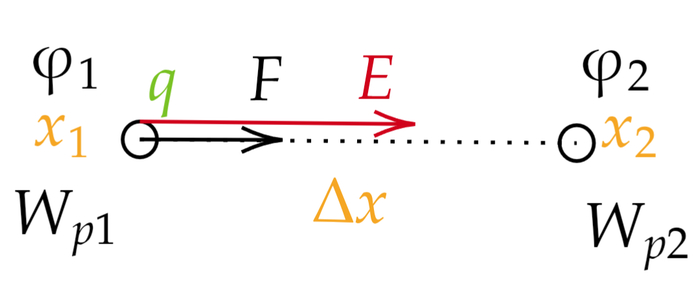
Рассмотрим перемещение заряда q из точки x₁ в точку x₂:
- Потенциальная энергия в точке 1: Wₚ₁
- Потенциальная энергия в точке 2: Wₚ₂
ΔWₚ=Wₚ₂-Wₚ₁

Работа поля:
A = Wₚ₁ - Wₚ₂ = -ΔWₚ
(Поле тратит потенциальную энергию, совершая работу)

Связь силы, работы и потенциала:
На заряд q действует сила:
F = q·E

Работа этой силы:
A = F·Δx = q·Eₓ·Δx,
где Δx = x₂ - x₁

Таким образом:
-ΔWₚ = q·Eₓ·Δx

Важные моменты:
При A > 0 (поле совершает работу) → ΔW < 0 (потенциальная энергия убывает)
Потенциальная энергия заряда в электрическом поле прямо пропорциональна величине заряда.
Потенциальная энергия зависит от выбора нулевого уровня, то есть, определяется с точностью до константы C:
Wₚ₁ = -q·Eₓ·x₁ + C
Wₚ₂ = -q·Eₓ·x₂ + C
Разность Wₚ₁ и Wₚ₂ от выбора нулевого уровня не зависит.

Потенциал:
φ = Wₚ / q

Если подставить выражение для потенциальной энергии, то φ = ( -q·Eₓ·x+ С) / q

Таким образом:
φ= -Eₓ·x + С

Введем понятие разности потенциалов:
Δφ = φ₁ - φ₂
Разность потенциалов является абсолютной величиной, константы сокращаются.
Обращаю внимание на то, что вычитаем из
φ₁ - φ₂, а не наоборот.

Работа через разность потенциалов:
A = q·Eₓ·Δx = q·(φ₁ - φ₂) = q·Δφ

Если сократить на q:
Eₓ·Δx = Δφ →Eₓ = Δφ /Δx

Направление поля:
Напряженность E направлена в сторону убывания потенциала.
(φ₁ > φ₂ → Eₓ > 0)

Теперь, перейдем к понятию напряжение.
Часто разность потенциалов называют напряжением. Но эти понятия - не тождественные. Напряжение - более общее.

Рассмотрим различия:

Разность потенциалов между двумя точками - это работа, которую совершает электростатическое поле при перемещении единичного положительного заряда из одной точки в другую.

Напряжение - это полная работа по переносу заряда:
1. Работа электростатического поля
2. Работа сторонних сил

То есть, разность потенциалов определяется электростатическими силами.
А, напряжение определяется всеми силами действующими на заряд.

В данном случае они совпадают:
Δφ=U
Eₓ = Δφ /Δx →Eₓ = U / Δx
Мы получили формулу связи напряжения и напряженности для однородного электростатического поля или стационарного тока в проводнике.

Показать полностью 1

fizikaVzametkah

3 месяца назад

#Заметка10. Направление напряженности электростатического поля точечного заряда⁠⁠

Электрические заряды действуют друг на друга опосредованно, с помощью электрического поля. Каждый заряд создает свое электрическое поле. Помещая пробный заряд q₂ в поле другого заряда q₁, мы можем оценить воздействие этого поля на заряд q₂. Поле заряда q₁ будет действовать на заряд q₂ с силой некоторой величины F̅₂₁, которая описывается законом Кулона. #Заметка5. Закон Кулона . Отношение действующей на пробный заряд q₂ силы Кулона F̅₂₁ к величине этого заряда называется напряженностью.

E̅₁ = F̅₂₁ /q₂ .

Здесь можно более подробно ознакомиться с определением напряженности. #Заметка9. О напряженности электрического поля

А сейчас поговорим о направлении напряженности поля точечного заряда.

Вектор напряженности E̅₁ в произвольной точке поля, например, в точке расположения пробного заряда q₂ направлен вдоль прямой, соединяющей заряды q₂ и q₁. Запишем выражение для напряженности поля точечного заряда в векторной форме. Для этого воспользуемся определением напряженности и законом Кулона в векторной форме. #Заметка6. Закон Кулона в векторной форме
Итак,

#Заметка10. Направление напряженности электростатического поля точечного заряда Физика, Электростатика, ЕГЭ, Репетитор, Заметки, Напряженность, Заряд, ОГЭ, Длиннопост

где:
r̄₂₁ - вектор указывающий на заряд q₂ и выходящий из заряда q₁ (точку расположения q₁ принимаем за начало координат).

Если заряд q₁>0, тогда, множитель перед вектором r̄₂₁ оказывается положительным (поскольку все остальные величины: k, ε, r₂₁ положительны). Значит, вектор напряженности E̅₁ сонаправлен с вектором r̄₂₁.

Т.о., вектор E̅₁ выходит из заряда q₁

Если заряд q₁<0, тогда, множитель перед вектором r̄₂₁ оказывается отрицательным (поскольку все остальные величины: k, ε, r ₂₁ положительны). Значит, вектор напряженности E̅₁ направлен против вектора r̄₂₁.

Т.о., вектор E̅₁ входит в заряд q ₁

На примере положительных зарядов рассмотрим понятие силовых линий (или линий напряженности).

Для положительных зарядов напряженность поля увеличивается при приближении к заряду, E̅~1/r² . Таким образом, в точках, расположенных на разных удаленностях от заряда, вектора E̅ будет иметь разную длину (чем ближе к заряду, тем больше длина).

Конечно, можно изображать множества векторов разных длин направленных вдоль радиуса, соответствующих разным удаленностям от заряда. Но, на практике намного нагляднее вместо множества векторов изображать непрерывную силовую линию. (Особенно, рассматривая поля более сложной конфигурации, чем поле точечного положительного заряда)

Силовая линия - линия, касательные к которой в каждой точке совпадают с направлением вектора E̅. Силовые линии электростатического поля выходят из положительных зарядов и входят в отрицательные.

Для положительного точечного заряда силовые линии - это прямые, выходящие из заряда во все стороны; множества векторов напряженности (соответствующие множествам точек различной удаленности от заряда) в данном случае, направлены вдоль силовых линий.

#ФизикаПоПорядку #Электростатика #ЗаметкиРепетитора #ЕГЭ #ФИЗИКА

Показать полностью 4

Физика Электростатика ЕГЭ Репетитор Заметки Напряженность Заряд ОГЭ Длиннопост

fizikaVzametkah

4 месяца назад

#Заметка9. О напряженности электрического поля⁠⁠

Пусть точечный заряд q₁ создает электрическое поле напряженностью E̅₁. Поместим в это поле на расстоянии r от q₁ пробный заряд q₂. На заряд q₂ со стороны заряда q₁ будет действовать сила Кулона F̅₂₁ .
(о силе Кулона более подробно можно почитать в предыдущих заметках:
#Заметка6. Закон Кулона в векторной форме )

Напряженность E̅₁ - отношение силы F̅₂₁, с которой поле действует на точечный заряд q₂ к величине этого заряда. Напряженность называют силовой характеристикой поля. Это векторная величина. Значение напряженности:

E₁ = F₂₁/q₂ = k · |q₁|· |q₂| / ( |q₂| · r² ) = k · |q₁| / r²

Из формулы видно, что напряженность поля E₁ заряда q₁ НЕ зависит от величины пробного заряда q₂. Таким образом, напряженность характеризует поле, в которое помещен пробный заряд. Очевидно, это поле существует и в отсутствие пробного заряда. Пробный заряд нам просто позволяет обнаружить его, поскольку на заряд со стороны поля действует сила.

Если помещать заряды различной величины на место заряда q₂, сила действующая на заряд будет изменяться пропорционально величине этого заряда.

F̅₂₁ = q₂ · E̅₁

Значение напряженности зависит от координаты рассматриваемой точки. Помещая пробный заряд q₂ в различные точки пространства, мы можем исследовать изменение напряженности поля E̅₁ в пространстве.

Единица измерения E̅ в СИ E̅ - [Н/Кл] или [В/м].

О направлении вектора напряженности поговорим в следующей заметке.

Показать полностью 1

Физика ЕГЭ Электричество Электростатика Заметки Репетитор

fizikaVzametkah

4 месяца назад

#Заметка8. ЕГЭ. Электростатика. №14. Разбор⁠⁠

Разберем пример из сборника по подготовке к ЕГЭ под редакцией Демидовой.

Условие:

Две маленькие, закрепленные бусинки, расположенные в точках A и B, несут на себе заряды +q>0 и−2q соответственно(см.рис.1) Точка С находится посередине между бусинками A и B.

#Заметка8. ЕГЭ. Электростатика. №14. Разбор Физика, Электростатика, Репетитор, ЕГЭ, Длиннопост

Рис. 1. Иллюстрация к условию

Из приведенного ниже списка выберите вcе правильные утверждения.

На бусинку B со стороны бусинки A действует сила Кулона, направленная горизонтально вправо.
Напряжённость результирующего электростатического поля в точке C направлена горизонтально вправо.
Модули сил Кулона, действующих на бусинки, одинаковы.
Если бусинки соединить тонкой медной проволокой, они будут отталкиваться друг от друга.
Если бусинки соединить незаряженной стеклянной палочкой, их заряды станут равными.

Решение:

1.) Определим направление силы Кулона в точке В.

Мы знаем, что два заряда разного знака стремятся притянуться друг к другу.

На основании этого утверждения, мы можем сразу сказать, что сила Кулона F̄ᵦₐ , действующая на заряд qᵦ cо стороны заряда qₐ , направлена влево, то есть, по направлению к заряду qₐ.

Но, еще мы можем подойти к этому же ответу, не опираясь на данное утверждение, а обратившись к закону Кулона в векторной форме. Пусть вектор r̄ᵦₐ указывает на qᵦ со стороны qₐ, т.е. направлен вправо, тогда:

мы видим qₐ•qᵦ<0,значит F̄ᵦₐ↑↓r̄ᵦₐ (сила Кулона направлена влево)

Утверждение 1 - неверно.

Более подробно о векторной форме закона Кулона можно прочитать в моей заметке #Заметка6. Закон Кулона в векторной форме

2.) Определим напряженность в точке С.

Каждый заряд создает свое электрическое поле.

Заряд qₐ – поле напряженностью Ēₐ

Заряд qᵦ – поле напряженностью Ēᵦ

Результирующая напряженность Ē𝛴 определяется по принципу суперпозиции как геометрическая сумма напряженностей Ēₐ и Ēᵦ.

В точке С вектор напряженности поля Ēₐ положительного заряда qₐ направлен от данного заряда, вдоль прямой, соединяющей qₐ и рассматриваемую точку С. (т.е. вправо).

В точке С вектор напряженности поля Ēᵦ отрицательного заряда qᵦ направлен к данному заряду, вдоль прямой, соединяющей qᵦ и рассматриваемую точку точку С (т.е. вправо).

Т.о., суммарная напряженность Ē𝛴 = Ēₐ + Ēᵦ направлена вправо, в сторону заряда qᵦ.

Утверждение 2 - верно.

Рис. 2. Иллюстрация к ответам на п.1 и п.2

3.) Определим модули сил.

Запишем закон Кулона.

На заряд qᵦ со стороны заряда qₐ действует сила F̄ᵦₐ:

по 3-му закону Ньютона сила с которой на заряд qₐ действует поле заряда qᵦ :

Fₐᵦ =-Fᵦₐ

т.о. данные силы равны по модулю | Fₐᵦ | = | Fᵦₐ |

Более того, мы можем записать выражение для расчета силы Fₐᵦ по закону Кулона и увидеть, что в него входят все те же самые величины, что и в формуле выше для силы Fᵦₐ.

Утверждение 3 - верно.

4.) Воспользуемся законом сохранения электрического заряда.

Медь является проводником. Соединение проводником вызовет перераспределение зарядов.

По закону сохранения электрического заряда: в изолированной системе алгебраическая сумма зарядов остается неизменной.
Из условия мы видим, что бусины можно считать точечными зарядами, ввиду их малого размера. Т.о. точки А и Б для зарядов не имеют никаких отличий, поэтому после их соединения заряд распределиться поровну между ними:

q’ₐ = q'ᵦ= (qₐ+qᵦ) / 2 = (+q - 2q) / 2= - q / 2= - 0.5 q

Значит, мы получили две отрицательно заряженных точки, а, как мы знаем, заряды одного знака отталкиваются.

Утверждение 4 - верно.

5.) Стекло не вызовет перераспределение зарядов, поскольку является диэлектриком. Заряды равными не станут.

Утверждение 5 - неверно.

Показать полностью 3

Физика Электростатика Репетитор ЕГЭ Длиннопост

fizikaVzametkah

4 месяца назад

#Заметка7. Направление силы Кулона⁠⁠

В предыдущем материале можно прочитать
#Заметка6. Закон Кулона в векторной форме
как мы получили выражение:
─────────────────────────────────
𐨸 F₁₂ = k • q₁• q₂ • 𐨸r₁₂ / ε • r³₁₂
─────────────────────────────────
Аналогично формула будет выглядеть для силы 𐨸F₂₁.
Примем во внимание, что вектора 𐨸r₁₂ , 𐨸r₂₁ направлены встречно
𐨸r₁₂
❶⟵❷

𐨸 𐨸r₂₁
❶⟶❷
Проанализируем как силы будут направлены относительно друг друга:
I. Если оба заряда одного знака
⊕ ⊕ либо ⊖ ⊖, то :
🔹 сила 𐨸F₁₂, приложенная к заряду q₁ сонаправлена с вектром 𐨸r₁₂, указывающим на заряд q₁ со стороны q₂
𐨸r₁₂
𐨸 F₁₂ ⟵ ❶ ⟵ ❷

🔹 сила 𐨸F₂₁, приложенная к заряду q₂ сонаправлена с 𐨸r₂₁ , указывающим на заряд q₂ со стороны q₁
𐨸r₂₁
❶ ⟶ ❷ ⟶ 𐨸F₂₁

Таким образом :
─────────────────────────────────
При одноименных зарядах -
кулоновские силы 𐨸 F₁₂ , 𐨸 F₂₁ направлены друг от друга и заряды отталкиваются!

𐨸F₁₂ ⟵ ❶ ❷ ⟶ 𐨸F₂₁

─────────────────────────────────
II. Если заряды разного знака
⊕ ⊖ либо ⊖ ⊕ , то:
🔹 сила 𐨸F₁₂, приложенная к заряду q₁, направлена против вектора 𐨸r₁₂, указывающим на заряд q₁ со стороны q₂
𐨸r₁₂
❶ 𐨸F₁₂⟶ ⟵❷

🔹 сила 𐨸F₂₁, приложенная к заряду q₂ направлена против ввектора 𐨸r₂₁, указывающим на заряд q₂ со стороны q₁.

𐨸r₂₁
❶⟶ ⟵ 𐨸F₂₁❷

Таким образом :
─────────────────────────────────
При разноименных зарядах -
кулоновские силы 𐨸 F₁₂, 𐨸 F₂₁ направлены друг к другу и заряды притягиваются!

❶ 𐨸F₁₂⟶ ⟵ 𐨸F₂₁❷

─────────────────────────────────

В следующей заметке разберем практический пример.

#ФизикаПоПорядку #Электростатика #ЗаметкиРепетитора

Показать полностью

Физика ЕГЭ Репетитор Электростатика Кулон Текст

fizikaVzametkah

4 месяца назад

#Заметка6. Закон Кулона в векторной форме⁠⁠

Из материала #Заметка5. Закон Кулона мы знаем, что заряд q₂ своим электрическим полем 𐨸Е₂ воздействует на заряд q₁ с силой Кулона 𐨸F₁₂.
Аналогично, со стороны эл.поля 𐨸Е₁ (заряда q₁) на заряд q₂ будет действовать сила Кулона 𐨸F₂₁.
Легко убедиться, что | F₂₁ | = | F₁₂ |.
Поговорим о направлении действия кулоновских сил.
─────────────────────────────────
Силы взаимодействия двух точечных неподвижных зарядов направлены вдоль прямой, соединяющей их.
─────────────────────────────────
Можно увидеть, что направление сил противоположно друг другу,
согласно 3-му закону Ньютона:
─────────────────────────────────
            𐨸F₂₁ = — 𐨸F₁₂
─────────────────────────────────
Заряды находятся на расстоянии r друг от друга. Воспользуемся понятием радиус - вектора.
─────────────────────────────────
Радиус-вектор задает положение точки в пространстве относительно другой точки, принятой за начало координат.
─────────────────────────────────
Пусть радиус-вектор 𐨸 r₁₂ указывает на q₁ и выходит из q₂.

           𐨸r₁₂
       ❶⟵❷

Учтем 𐨸r₁₂ в законе Кулона:
● домножим числитель на 𐨸r₁₂
● в знаменателе квадрат расстояния превратим в куб
● с обоих зарядов уберем модули

Получим: закон Кулона в векторной форме:
─────────────────────────────────

         𐨸F₁₂ = k • q₁• q₂• 𐨸r₁₂ / ε • r³₁₂

─────────────────────────────────
Мы видим, что:
А.) Если:
— оба заряда положительные ⊕ ⊕
— оба заряда отрицательные ⊖ ⊖, то:
кулоновская сила 𐨸F₁₂, действующая на заряд q₁ со стороны заряда q₂, сонаправлена с радиус вектором 𐨸r₁₂, указывающим на q₁ и выходящим из q₂,
─────────────────────────────────
🔹Если q₁• q₂ > 0, то 𐨸F₁₂ ↑↑ q₁• q₂ • 𐨸r₁₂
─────────────────────────────────

Б.) Если:
— знаки зарядов q₁ и q₂ различны ⊕ ⊖ , то:
кулоновская сила 𐨸F₁₂ противоположно направлена радиус-вектору 𐨸r₁₂
─────────────────────────────────
🔹 Если q₁ • q₂ < 0, то 𐨸 F₁₂ ↓↑ q₁ • q₂ • 𐨸r₁₂
─────────────────────────────────

Аналогичные выводы можно сделать относительно силы 𐨸F₂₁ и вектора 𐨸r₂₁

Рассматриваем направления сил 𐨸F₁₂ и 𐨸F₂₁ относительно друг друга и делаем выводы, когда заряды притягиваются и когда отталкиваются в следующей заметке. #Заметка7

#ФизикаПоПорядку #Электростатика #ЗаметкиРепетитора

Показать полностью

Физика ЕГЭ Репетитор Электростатика Кулон Текст

fizikaVzametkah

4 месяца назад

#Заметка5. Закон Кулона⁠⁠

Начнем разбор некоторых понятий из Электростатики с Закона Кулона.
Закон Кулона применим для определения силы взаимодействия между неподвижными точечными зарядами

Пусть заряд q₁ создает электрическое поле напряжённостью 𐨸Е₁.
На расстоянии r от заряда q₁ поместим заряд q₂.
Заряд q₂ создает поле напряжённостью 𐨸Е₂.
Тогда, со стороны поля 𐨸Е₂ (заряда q₂) на заряд q₁ будет действовать сила Кулона 𐨸F₁₂.
─────────────────────────────────

Сила Кулона 𐨸 F₁₂— сила взаимодействия между двумя точечными зарядами q₁ и q₂, находящихся на расстоянии r друг от друга.

─────────────────────────────────
Численное значение силы можно определить по формуле:
─────────────────────────────────

                F₁₂=k•|q₁|•|q₂| / εr²

─────────────────────────────────
где:
ε — диэлектрическая проницаемость среды, показывает во сколько раз сила взаимодействия зарядов уменьшается в некоторой среде относительно силы их взаимодействия в вакууме. Безразмерная величина.
Для вакуума ε=1.

k — коэффициент пропорциональности, в системе единиц СИ:
k = 1/(4π•ε₀) = 9•10⁹ [ Н•м²/ Кл²] , в котором:

ε₀ — электрическая постоянная:
ε₀ = 8,85•10⁻¹² [Ф/м]

─────────────────────────────────

В таком виде формула позволяет определить значение силы Кулона, но не ее направление.

О том, как определить направление силы Кулона написано в следующем материале #Заметка6. Закон Кулона в векторной форме.

Показать полностью

Физика ЕГЭ Репетитор Электростатика Текст

fizikaVzametkah

4 месяца назад

#Заметка4. О важности владения формальными навыками при решении задач по физике⁠⁠

Каждый, кто регулярно решает задачи по физике, сталкивается с моментом, когда непонятно, с чего начать 😅. Это абсолютно нормально!

Чтобы таких ситуаций было меньше, нужно:
▪️ Твёрдо знать базовые принципы — без этого никуда 🚫
▪️ Понимать: важнее самого решения — правильная подготовка к нему, то есть точное понимание условия! 🔍

Важно понимать, для чего нужно соблюдать формальные принципы в оформлении решений 📝 и уделять внимание таким вещам.
Простые и избитые вещи вроде аккуратного написания "Дано", "Решение", "Действия с единицами измерения" и "Ответ" несут важную функцию:
- Помогают не упустить ключевые параметры
- Минимизируют ошибки по невнимательности
- Позволяют четче сформировать свое восприятие условия

💡 Запомните:
- Правильно понятое условие — это 50% успеха
- Остальные 50% — знание законов и умение их применять

Более подробно, как облегчить себе понимание условий и минимизировать ошибки, описано в моих постах:
1️⃣ Алгоритм подготовки задачи к решению 🛠️
#Заметка2. Универсальный алгоритм по ПОДГОТОВКЕ задачи к решению
2️⃣ Методы самопомощи, когда накрыл "тупняк" 💪
#Заметка3. Поговорим о критической ситуации при решении задач

Это сэкономит ваши нервы 🧘 и повысить шансы получить верный ответ! ✅

#ФизикаПоПорядку #МетодикаРешения #ЗаметкиРепетитора

Показать полностью

Физика ЕГЭ Репетитор Текст

Отличная работа, все прочитано!

1 2